6.1平均数 课件（共24张PPT）

(共24张PPT)
导入新课
观察与思考
右图表示的是甲、乙、丙三人的射击成绩，谁的成绩更好，谁更稳定？你是怎么判断的？除了直观感觉外，我们如何用量化的数据来刻画“更好”“更稳定”呢？
6.1 平均数
第六章 数据的分析
学习目标
1.掌握算术平均数的概念，会求一组数据的算术平均数．（重点）
2.会用算术平均数解决实际生活中的问题．（难点）
讲授新课
1. 定义：一般地，对于n个数x1，x2，…，xn，我们
把 (x1＋x2＋…＋xn)叫做这n个数的算术平均数；
简称平均数；记为 ．
算术平均数
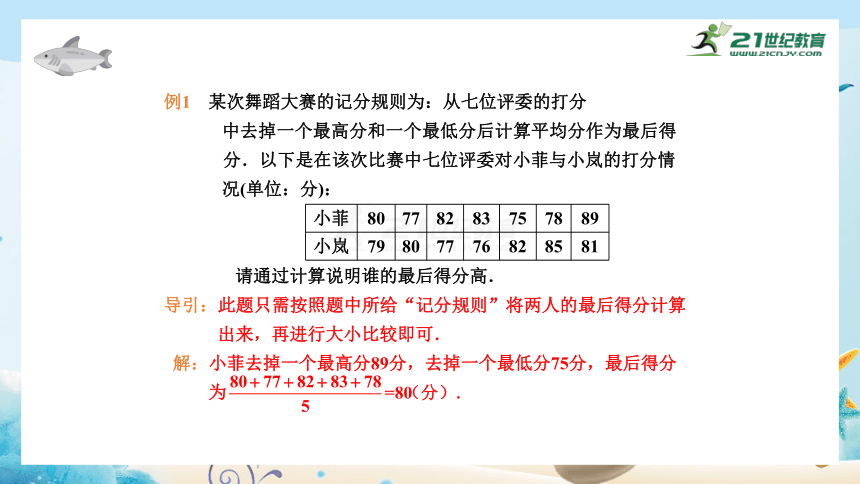
例1 某次舞蹈大赛的记分规则为：从七位评委的打分
中去掉一个最高分和一个最低分后计算平均分作为最后得
分．以下是在该次比赛中七位评委对小菲与小岚的打分情
况(单位：分)：
请通过计算说明谁的最后得分高．
导引：此题只需按照题中所给“记分规则”将两人的最后得分计算
出来，再进行大小比较即可．
解：小菲去掉一个最高分89分，去掉一个最低分75分，最后得分
为
小菲 80 77 82 83 75 78 89
小岚 79 80 77 76 82 85 81
小岚去掉一个最高分85分，去掉一个最低分76分，
最后得分为
因为80分＞79.8分，所以小菲的最后得分高．
例2 在一次数学考试中，抽取了20名学生的试卷进行分析．这20
名学生的数学成绩(单位：分)分别为87，85，68，72，58，
100，93，97，96，83，51，84，92，62，83，79，74，72，
65，79[注：这份试卷满分100分，60分以上(含60分)为合格]．
(1)求这20名学生的平均成绩；
(2)求这20名学生的合格率．
解：(1)将原数据都减去80，得到新数据为7，5，－12，－8，
…，－15，－1.
所以新数据的平均数
(－15)＋(－1)]÷20＝－1．
所以原数据的平均数
即这20名学生的平均成绩为79分．
(2)这20名学生的合格率为
新数据法求平均数的方法：
1. 确定一个常数（这组数据在这个常数附近波动且
较“整”）；
2. 用每个数据减去这个常数得到一组新数，并求出
这组新数的平均数；
3. 原数据的平均数等于新数据的平均数加上这个常
数
总结
在实际问题中，一组数据里的各个数据的“重要程度” 未必相同.因而，在计算这组数据的平均数时，往往给每个数据一个“权”．
一起来看看下面的例子
二、加权平均数
例2 某广告公司欲招聘广告策划人员一名，对A,B,C三名候选人进行了三项素质测试，他们的各项测试成绩如下表所示：
测试项目 测试成绩 A B C
创新 72 85 67
综合知识 50 74 70
语言 88 45 67
（1）如果根据三项测试的平均成绩决定录用人选，那么谁将被录用？
（2）根据实际需要，公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人的测试成绩，此时谁将被录用？
解:
（1）A的平均成绩为（72+50+88）/3=70(分).
B的平均成绩为（85+74+45）/3=68(分).
C的平均成绩为（67+70+67）/3=68(分).
由70>68，故A被录用.
（2）根据题意，
A的测试成绩为
B的测试成绩为
C的测试成绩为
因此候选人B将被录用.
4，3，1 分别是创新、综合知识、语言三项测试成绩的权，而称（72×4+50×3+88×1）÷（4+3+1）
为A的三项测试成绩的加权平均数.
例3 老师对同学们每学期总评成绩时，并不是简单地将一个学生的平时成绩与考试成绩相加除以2而是按照“平时练习占 40%, 考试成绩占60% ”的比例计算，其中考试成绩更为重要.这样，如果一个学生的平时成绩为70分，考试成绩为90分，那么他的学期总评成绩就应该为多少呢？
解:
该同学的学期总评成绩是:
70×30%
=82(分)
+
90×60%
加权平均数
权 重
权重的意义:
各个数据在该组数据中所占有的不同重要性的反映.
加权平均数的意义:
按各个数据的权重来反映该组数据的总体平均大小情况.
　　一般地，若n个数x1，x2，…，xn的权分别
是w1，w2，…，wn，则
叫做这n个数的加权平均数．
知识要点
做一做
60％
40％
在2018年中山大学数科院的研究生入学考试中，两名考生在笔试、面试中的成绩（百分制）如下图所示，你觉得谁应该被录取？
考生 笔试 面试
甲 86 90
乙 92 83
（笔试和面试的成绩分别按60%和40%计入总分）
6
：
4
解：根据题意，求甲、乙成绩的加权平均数，得
答：因为_____＞_____，所以_____将被录取.
乙
当堂练习
1.某次考试，5名学生的平均分是82，除甲外，其余4名学生的平均分是80，那么甲的得分是（ ）
A.84 B. 86 C. 88 D. 90
D
2.李大伯有一片果林，共有80棵果树．某日，李大伯开始采摘今年第一批成熟的果子，他随机选取2棵果树共摘得10个果子，质量分别为（单位：㎏）：0.28，0.26，0.24，0.23，0.25，0.24，0.26，0.26，0.25，0.23．以此估算，李大伯收获的这批果子的单个质量和总质量分别约为（　　）
A.0.25 ㎏，200 ㎏ B.2.5 ㎏，100 ㎏
C.0.25 ㎏，100 ㎏ D.2.5 ㎏，200 ㎏
C
3.若x1,x2,…, xn的平均数为a，
(1)则数据x1+3,x2+3,…,xn+3的平均数为 .
(2)则数据10x1,10x2,… ,10xn 的平均数为 .
a+3
10a
课堂总结
平均数
算术平均数
加权平均数
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php