2021-2022人教版(2019)高中数学选择性必修第三册6.2.1-6.2.2排列与排列数 课件(共20张PPT)
文档属性
| 名称 | 2021-2022人教版(2019)高中数学选择性必修第三册6.2.1-6.2.2排列与排列数 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 20:26:04 | ||
图片预览







文档简介
(共20张PPT)
第六章 记数原理
6.2.1-6.2.2 排列与排列数
新课引入
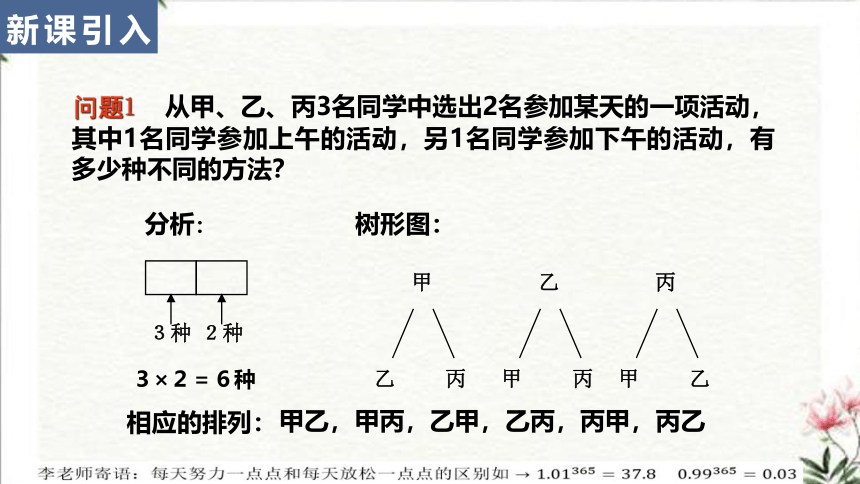
问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的方法?
3种
2种
3×2=6种
甲
乙
丙
乙
甲
丙
丙
甲
乙
分析:
树形图:
相应的排列:
甲乙,甲丙,乙甲,乙丙,丙甲,丙乙
新课引入
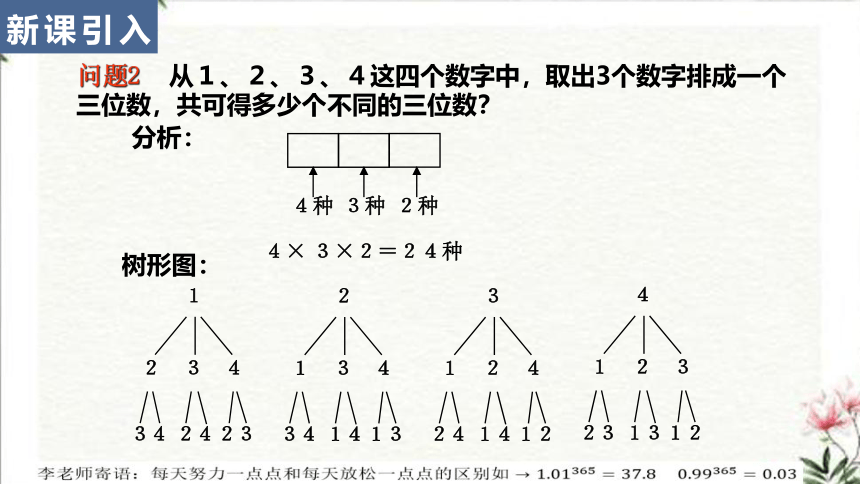
4种
3种
4× 3×2=24种
2种
问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
分析:
1
2
3
4
3
4
2
4
2
3
2
1
3
4
3
4
1
4
1
3
3
1
2
4
2
4
1
4
1
2
4
1
2
3
2
3
1
3
1
2
树形图:
课堂探究
一般地,从n个不同元素中取出m(m≤n)个元素,并按照___________排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列包括两个方面:取出元素→按一定顺序排列
同学们猜猜两个排列相同的条件是什么?
元素相同,且排列顺序相同
例题解析
例1:判断下列“事情”是否为排列:
是
是
是
否
(2)从全班40名同学中挑选4人;
(4)从某10人中选取4人参加4×100m接力赛;
(3)将3本不同的书分发给3个人.
(1)5人站成一排照相;
课堂探究
练习 下列问题是排列问题吗?
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
课堂探究
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
问1:从3个不同的元素中取2个元素的排列数?
问2:从5个不同的元素中取4个元素的排列数?
课堂探究
课堂探究
练习 下列问题是排列问题吗?若是,用排列公式表示出来
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
课堂探究
课堂探究
练习 下列问题是排列问题吗?若是,用排列公式表示出来
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
=50×49 ×48
=4×3×2
=5×4
=10×9×8
=4×3×2×1
全排列:一般地n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列。
n!(n的阶乘)
课堂探究
课堂探究
例题解析
例3.有4个男生和3个女生排成一排,按下列要求各有多少种不同排法:
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾;
(3)三个女生排在一起;
(4)三个女生两两都不相邻;
对于相邻问题,常用“捆绑法”
对于不相邻问题,常用“插空法”
例题解析
变式练习:有6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有 种.
例题解析
变式练习:有6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有 种.
解:分步计数:第一步:将甲、乙两本书摆放在两端,有 =2种摆法.
第二步:将丙、丁两本书看成一个整体,考虑两本书顺序,有 =2种摆法.
第三步:将丙、丁这个整体与另外两本书全排列,摆放在中间3个位置,有 =6种摆法.
共有 = 2×2×6=24 种不同的摆放方法.
例题解析
1、计算:(1) (2) (3) (4)
2、求证:(1) (2)
练习巩固
答案:C
当堂达标
3.从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为( )
A.5 B.10 C.20 D.60
练习巩固
A.(20-m)(21-m)(22-m)(23-m)(24-m)(25-m)
B.(20-m)(19-m)(18-m)(17-m)(16-m)
C.(20-m)(19-m)(18-m)(17-m)(16-m)(15-m)
D.(19-m)(18-m)(17-m)(16-m)(15-m)
答案:C
练习巩固
课堂小结
你收获了什么?
作业1:名师导学
作业2:书本练习P16、20
作业3:
作业布置
第六章 记数原理
6.2.1-6.2.2 排列与排列数
新课引入
问题1 从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的方法?
3种
2种
3×2=6种
甲
乙
丙
乙
甲
丙
丙
甲
乙
分析:
树形图:
相应的排列:
甲乙,甲丙,乙甲,乙丙,丙甲,丙乙
新课引入
4种
3种
4× 3×2=24种
2种
问题2 从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
分析:
1
2
3
4
3
4
2
4
2
3
2
1
3
4
3
4
1
4
1
3
3
1
2
4
2
4
1
4
1
2
4
1
2
3
2
3
1
3
1
2
树形图:
课堂探究
一般地,从n个不同元素中取出m(m≤n)个元素,并按照___________排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列包括两个方面:取出元素→按一定顺序排列
同学们猜猜两个排列相同的条件是什么?
元素相同,且排列顺序相同
例题解析
例1:判断下列“事情”是否为排列:
是
是
是
否
(2)从全班40名同学中挑选4人;
(4)从某10人中选取4人参加4×100m接力赛;
(3)将3本不同的书分发给3个人.
(1)5人站成一排照相;
课堂探究
练习 下列问题是排列问题吗?
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
课堂探究
从n个不同的元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同的元素中取出m个元素的排列数。用符号 表示。
问1:从3个不同的元素中取2个元素的排列数?
问2:从5个不同的元素中取4个元素的排列数?
课堂探究
课堂探究
练习 下列问题是排列问题吗?若是,用排列公式表示出来
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
课堂探究
课堂探究
练习 下列问题是排列问题吗?若是,用排列公式表示出来
1、某班50人,从中选出3人分别担任班长、学习委员、生活委员,共有多少种安排方法?( )
2、从4种不同的蔬菜品种中选出3种,分别种植在不同土质的3块土地上进行试验,有多少种不同的种植方法?( )
3、从1、2、3、4、5中任取两个数字做除式,有多少个除式? ( )
4、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数作集合,有多少个集合?( )
5、集合A={0,1,2,3,4,5,6,7,8,9},从中任取3个数组成没有重复数字的三项数列,有多少个数列?( )
6、4位同学站成一排照相,有多少种不同的站法?( )
是
是
是
是
是
否
=50×49 ×48
=4×3×2
=5×4
=10×9×8
=4×3×2×1
全排列:一般地n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列。
n!(n的阶乘)
课堂探究
课堂探究
例题解析
例3.有4个男生和3个女生排成一排,按下列要求各有多少种不同排法:
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾;
(3)三个女生排在一起;
(4)三个女生两两都不相邻;
对于相邻问题,常用“捆绑法”
对于不相邻问题,常用“插空法”
例题解析
变式练习:有6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有 种.
例题解析
变式练习:有6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有 种.
解:分步计数:第一步:将甲、乙两本书摆放在两端,有 =2种摆法.
第二步:将丙、丁两本书看成一个整体,考虑两本书顺序,有 =2种摆法.
第三步:将丙、丁这个整体与另外两本书全排列,摆放在中间3个位置,有 =6种摆法.
共有 = 2×2×6=24 种不同的摆放方法.
例题解析
1、计算:(1) (2) (3) (4)
2、求证:(1) (2)
练习巩固
答案:C
当堂达标
3.从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为( )
A.5 B.10 C.20 D.60
练习巩固
A.(20-m)(21-m)(22-m)(23-m)(24-m)(25-m)
B.(20-m)(19-m)(18-m)(17-m)(16-m)
C.(20-m)(19-m)(18-m)(17-m)(16-m)(15-m)
D.(19-m)(18-m)(17-m)(16-m)(15-m)
答案:C
练习巩固
课堂小结
你收获了什么?
作业1:名师导学
作业2:书本练习P16、20
作业3:
作业布置
