2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.3.2等比数列的前n项和公式 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 951.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 20:28:26 | ||
图片预览






文档简介
(共16张PPT)
4.3.2 等比数列的前n项和公式
2020年关键词----抗疫
国内专家研究新型冠状病毒的 约为2。按平均传染周期为7天估算,在没有外力介入,同时所用人都没有免疫力的情况下,1个初始感染者为第一轮传染,这1人初始感染者再传染2个人为第二轮传染........依此类推第三轮为4人,第四轮为8人......此数列为等比数列。前两轮累计感染人数为1+2=3,前三轮累计感染人数为1+2+4=7.....前10轮累计感染人数为1+2+4+.....+ .借助等比数列求和,可知预测感染人数由一个初始感染者增加到1000万人大约需要20轮,即五个月时间。因此,国家做出重要指示,从2020年1月23日10日起,武汉正式封城。封一座城,护一国人,武汉是座英雄的城市。
学习目标
1.通过任务一,强化从情境中提炼数学列式的思想,规范错位相减法的书写步骤,再次体会公式推导过程,提升数学建模思想。
2.通过任务二,掌握等比数列的前n项和公式的计算,解决等比数列知三求二问题,提升数学运算的核心素养。
3.通过任务三,会运用等比数列求和公式解决相关计算,体会分类讨论思想,提升学生运算的核心素养。
情境引入
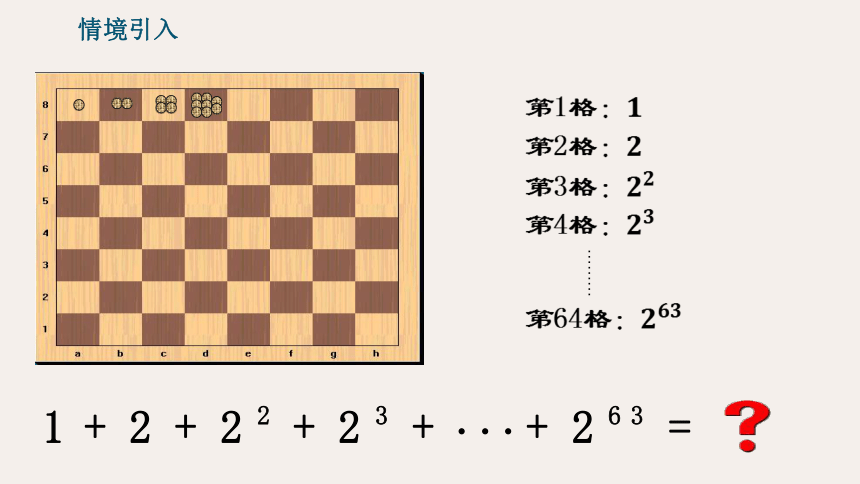
国际象棋的棋盘是正方形,黑白相间共64格,传说在很久以前,古印度国王在宫廷单调的生活中,发现了也就是现今的国际象棋如此的有趣之后,决定要重赏发明者——他的宰相,让他随意选择奖品,宰相说:“在棋盘的第1个格子里放1颗麦粒,第2个格子里放2颗麦粒,第3个格子里放4颗麦粒,依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64格。请给我足够的麦粒以实现上述要求。”国王一听,几颗麦粒,加起来也不过一小袋,他就答应了宰相的要求。请你想一想国王能实现他的诺言吗?
第1格:
第2格:
第3格:
第4格:
………
第64格:
情境引入
2S64= 2+22+23+···+263+264 ②
由②-①可得:
S64 =264-1
= 18446744073709551615 粒
1000粒麦粒重约为40克,那么这些麦粒的总质量就是7300多亿吨.而据统计2019年全世界小麦的年产量约为7.65亿吨!
错位相减法
任务一、公式的推导证明
如何计算等比数列的前n项和?
已知等比数列首项为,公比为q,则
两边同乘q:
①
②
(1 – q)Sn = a1 – a1qn
由①-②得:
当q=1时,
任务一、公式的推导证明
设等比数列{an}
它的前n项和是
注意
(1)等比数列求和时,应考虑q=1与q两种情况;
(2)推导等比数列前n项和公式的方法:错位相减法。
任务一、公式的推导证明
(3)步骤: 乘公比,错位写,对位减
任务二、公式应用解决知三求二问题
1.判断对错
任务二、公式应用解决知三求二问题
例1、已知数列{ }是等比数列。
(2)若 =27, = ,q<0,求
当堂检测
已知数列{ }是等比数列,若 =8,q= , = ,求n=( )
A. 4 B. 5 C. 6 D. 7
任务三、分类讨论解决计算问题
例2.已知等比数列的首项为-1,前n项和为
,若
=
求公比q
当堂检测
如果一个等比数列前4项和等于10,前8项和等于50,
求这个数列的公比q
任务三、分类讨论解决计算问题
总结
一种方法
一种思想
两个公式
知三求二
猜想:
第一个月存1分,
第二个月存2分,
第三个月存4分……
后一月存钱为前一月的2倍.
第一季度的存款数为:1+2+4=7
第二季度的存款数为:8+16+32=56
第三季度的存款数为:64+128+256=448
情境再思考:
猜想:
解析一:
解析二:
升华例题
4.3.2 等比数列的前n项和公式
2020年关键词----抗疫
国内专家研究新型冠状病毒的 约为2。按平均传染周期为7天估算,在没有外力介入,同时所用人都没有免疫力的情况下,1个初始感染者为第一轮传染,这1人初始感染者再传染2个人为第二轮传染........依此类推第三轮为4人,第四轮为8人......此数列为等比数列。前两轮累计感染人数为1+2=3,前三轮累计感染人数为1+2+4=7.....前10轮累计感染人数为1+2+4+.....+ .借助等比数列求和,可知预测感染人数由一个初始感染者增加到1000万人大约需要20轮,即五个月时间。因此,国家做出重要指示,从2020年1月23日10日起,武汉正式封城。封一座城,护一国人,武汉是座英雄的城市。
学习目标
1.通过任务一,强化从情境中提炼数学列式的思想,规范错位相减法的书写步骤,再次体会公式推导过程,提升数学建模思想。
2.通过任务二,掌握等比数列的前n项和公式的计算,解决等比数列知三求二问题,提升数学运算的核心素养。
3.通过任务三,会运用等比数列求和公式解决相关计算,体会分类讨论思想,提升学生运算的核心素养。
情境引入
国际象棋的棋盘是正方形,黑白相间共64格,传说在很久以前,古印度国王在宫廷单调的生活中,发现了也就是现今的国际象棋如此的有趣之后,决定要重赏发明者——他的宰相,让他随意选择奖品,宰相说:“在棋盘的第1个格子里放1颗麦粒,第2个格子里放2颗麦粒,第3个格子里放4颗麦粒,依此类推,每个格子里放的麦粒数都是前一个格子里放的麦粒数的2倍,直到第64格。请给我足够的麦粒以实现上述要求。”国王一听,几颗麦粒,加起来也不过一小袋,他就答应了宰相的要求。请你想一想国王能实现他的诺言吗?
第1格:
第2格:
第3格:
第4格:
………
第64格:
情境引入
2S64= 2+22+23+···+263+264 ②
由②-①可得:
S64 =264-1
= 18446744073709551615 粒
1000粒麦粒重约为40克,那么这些麦粒的总质量就是7300多亿吨.而据统计2019年全世界小麦的年产量约为7.65亿吨!
错位相减法
任务一、公式的推导证明
如何计算等比数列的前n项和?
已知等比数列首项为,公比为q,则
两边同乘q:
①
②
(1 – q)Sn = a1 – a1qn
由①-②得:
当q=1时,
任务一、公式的推导证明
设等比数列{an}
它的前n项和是
注意
(1)等比数列求和时,应考虑q=1与q两种情况;
(2)推导等比数列前n项和公式的方法:错位相减法。
任务一、公式的推导证明
(3)步骤: 乘公比,错位写,对位减
任务二、公式应用解决知三求二问题
1.判断对错
任务二、公式应用解决知三求二问题
例1、已知数列{ }是等比数列。
(2)若 =27, = ,q<0,求
当堂检测
已知数列{ }是等比数列,若 =8,q= , = ,求n=( )
A. 4 B. 5 C. 6 D. 7
任务三、分类讨论解决计算问题
例2.已知等比数列的首项为-1,前n项和为
,若
=
求公比q
当堂检测
如果一个等比数列前4项和等于10,前8项和等于50,
求这个数列的公比q
任务三、分类讨论解决计算问题
总结
一种方法
一种思想
两个公式
知三求二
猜想:
第一个月存1分,
第二个月存2分,
第三个月存4分……
后一月存钱为前一月的2倍.
第一季度的存款数为:1+2+4=7
第二季度的存款数为:8+16+32=56
第三季度的存款数为:64+128+256=448
情境再思考:
猜想:
解析一:
解析二:
升华例题
