2021-2022学年高中数学人教版A版(2019)选择性必修一1.4.2用空间向量研究距离、夹角问题 课件(共37张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一1.4.2用空间向量研究距离、夹角问题 课件(共37张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 20:54:27 | ||
图片预览










文档简介
(共37张PPT)
1.4.2 用空间向量研究距离、夹角问题
思考
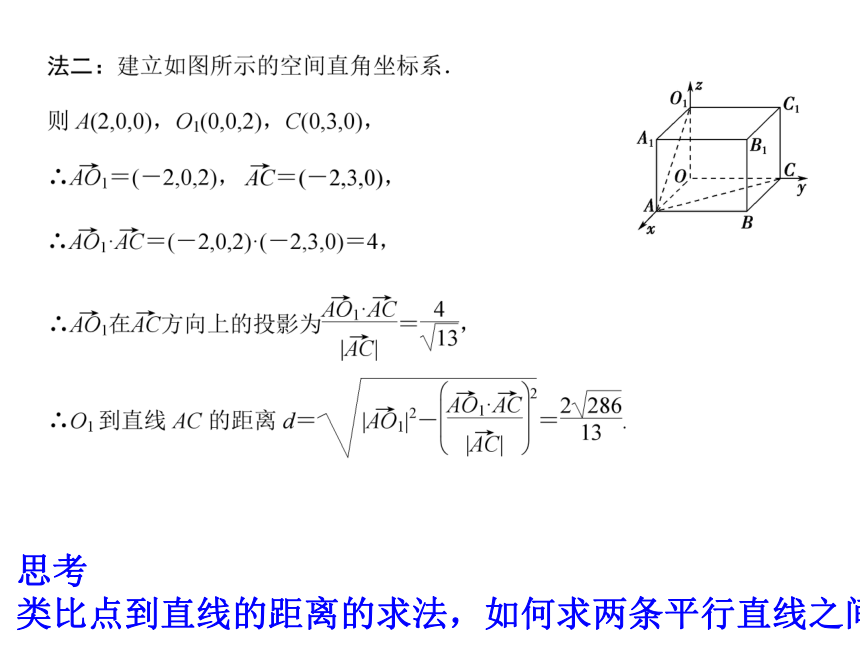
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
与用平面向量解决平面几何问题的“三步曲”类似,
我们可以得出用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题
中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及
它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
作业
P44 #13 #14
思考题:P44 #18(1)(2)
直线与直线所成的角、直线与平面所成的角、平面与平面的夹角
例7 如图1.4-19,在棱长为1的正四面体(四个面都是正三角形)
ABCD中, M, N分别为BC, AD的中点,
求直线AM和CN夹角的余弦值.
化为向量问题
进行向量运算
思考
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
回到图形问题
思考
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
解:化为向量问题
进行向量运算
回到图形问题
例9 图1.4-23为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°,已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0.01 N).
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
解决立体几何中的问题,可用三种方法:综合法、向量法、
坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
作业
P43 #9,P44 #15
思考题P44 #18(3)
1.4.2 用空间向量研究距离、夹角问题
思考
类比点到直线的距离的求法,如何求两条平行直线之间的距离?
与用平面向量解决平面几何问题的“三步曲”类似,
我们可以得出用空间向量解决立体几何问题的“三步曲”:
(1)建立立体图形与空间向量的联系,用空间向量表示问题
中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及
它们之间的距离和夹角等问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
作业
P44 #13 #14
思考题:P44 #18(1)(2)
直线与直线所成的角、直线与平面所成的角、平面与平面的夹角
例7 如图1.4-19,在棱长为1的正四面体(四个面都是正三角形)
ABCD中, M, N分别为BC, AD的中点,
求直线AM和CN夹角的余弦值.
化为向量问题
进行向量运算
思考
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
回到图形问题
思考
以上我们用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
解:化为向量问题
进行向量运算
回到图形问题
例9 图1.4-23为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°,已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0.01 N).
通过本节的学习,你对立体几何中的向量法是否有了一定的认识?请结合例题就下面的框图谈谈体会.
解决立体几何中的问题,可用三种方法:综合法、向量法、
坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
作业
P43 #9,P44 #15
思考题P44 #18(3)
