2021-2022学年高中数学人教版A版(2019)选择性必修一2.3直线的交点坐标与距离公式 课件(共72张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一2.3直线的交点坐标与距离公式 课件(共72张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 20:59:39 | ||
图片预览








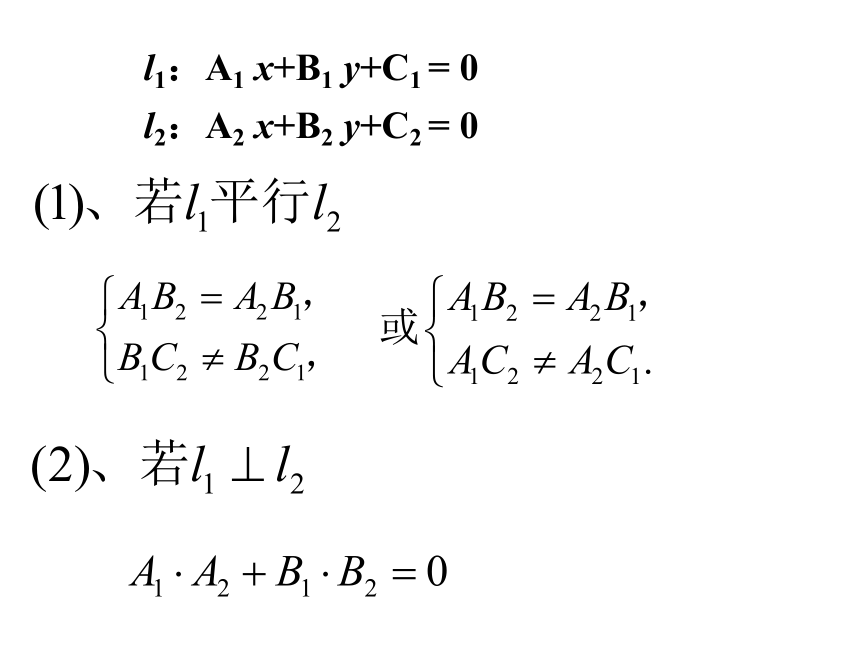

文档简介
(共72张PPT)
2.3 直线的交点坐标
与距离公式
P68
在平面几何中,我们对直线作了定性研究.引人平面直角坐标系后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标所满足的一个关系式.这样,我们可以通过方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点坐标,平面内与点、直线相关的距离问题等.
小结:方程组解的情况与方程组所表示的两条直线位置关系的联系?
解方程组
思考
你能用直线的斜率判断上述各对直线的位置关系吗?比较用斜率判断和解方程组 这两种方法,你有什么体会?
l1:A1 x+B1 y+C1 = 0
l2:A2 x+B2 y+C2 = 0
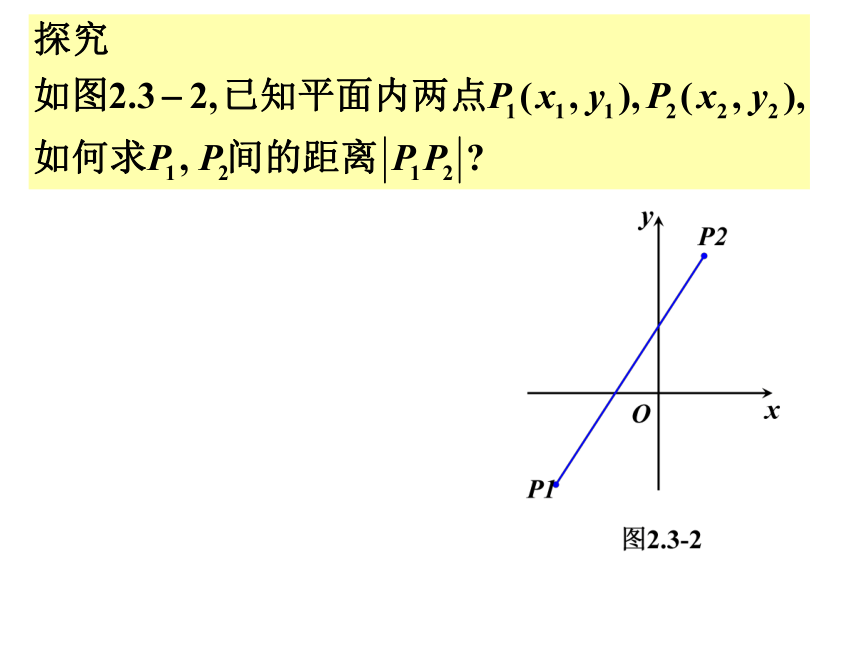
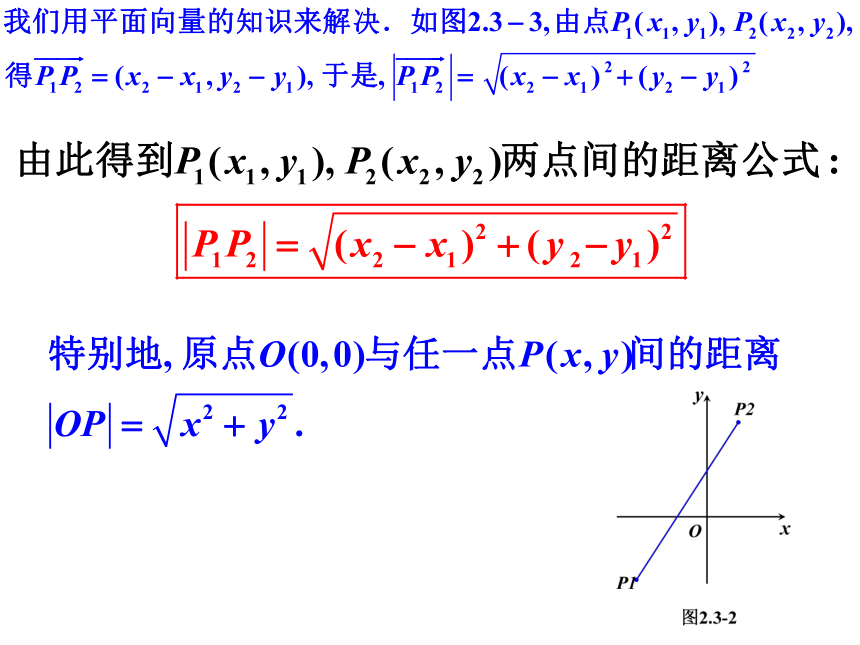
2.3.2 两点间距离公式
我们知道,在各种几何量中,直线段的长度是最基本的.所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
例4 用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把代数运算的结果 “翻译”成几何关系.
如何得到C点坐标
还有其它求C点坐标的方法吗?
即平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
思考
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
上述利用“坐标法”解决平面几何问题的基本步骤可以概括为
思考
根据例4的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
2.3.3 点到直线的距离公式
思考
上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗 由此能否给出简化运算的方法
探究
我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离
思考
比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算.除了上述两种方法,你还有其他推导方法吗
直线l有什么特性 由此你能给出简便解法吗
分析:由三角形面积公式可知,只要利用距离公式求出
边AB的长和边AB上的高即可.
你还有其他解法吗
2.3.4两条平行直线间的距离
前面我们已经得到了两点间的距离公式、点到直线的距离公式.关于平面上的距离问题,两条平行直线间的距离也是值得研究的.
两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长.
分析:两条平行直线间的距离即为这两条平行直线中的一条直线上的一点到另一条直线的距离.
作业
P79 第10题
如图,以边BC的中点为原点,
边BC所在直线为x轴建立平面直角坐标系
(1)如图,在平面直角坐标系中,
点A,B, C的坐标分别为(1,0), (1, 1), (0, 1).
连接AB,BC. 设P(x,y)为正方形内一点,则O
2.3 直线的交点坐标
与距离公式
P68
在平面几何中,我们对直线作了定性研究.引人平面直角坐标系后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标所满足的一个关系式.这样,我们可以通过方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点坐标,平面内与点、直线相关的距离问题等.
小结:方程组解的情况与方程组所表示的两条直线位置关系的联系?
解方程组
思考
你能用直线的斜率判断上述各对直线的位置关系吗?比较用斜率判断和解方程组 这两种方法,你有什么体会?
l1:A1 x+B1 y+C1 = 0
l2:A2 x+B2 y+C2 = 0
2.3.2 两点间距离公式
我们知道,在各种几何量中,直线段的长度是最基本的.所以,在解析几何中,最基本的公式自然是用平面内两点的坐标表示这两点间距离的公式.
例4 用坐标法证明:平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
分析:首先要建立适当的平面直角坐标系,用坐标表示有关的量,然后进行代数运算,最后把代数运算的结果 “翻译”成几何关系.
如何得到C点坐标
还有其它求C点坐标的方法吗?
即平行四边形两条对角线的平方和等于两条邻边的平方和的两倍.
思考
在“平面向量及其应用”的学习中,我们用“向量法”证明过这个命题.你能回忆一下证明过程吗 比较“坐标法”和“向量法”,你有什么体会
上述利用“坐标法”解决平面几何问题的基本步骤可以概括为
思考
根据例4的条件,你是否还有其他建立坐标系的方法 你能说说建立适当坐标系对证明的重要性吗
2.3.3 点到直线的距离公式
思考
上述方法中,我们根据点到直线距离的定义,将点到直线的距离转化为两点之间的距离,思路自然但运算量较大.反思求解过程,你发现引起复杂运算的原因了吗 由此能否给出简化运算的方法
探究
我们知道,向量是解决距离、角度问题的有力工具,能否用向量方法求点到直线的距离
思考
比较上述两种方法,第一种方法从定义出发,把问题转化为求两点间的距离,通过代数运算得到结果,思路自然;第二种方法利用向量投影,通过向量运算求出结果,简化了运算.除了上述两种方法,你还有其他推导方法吗
直线l有什么特性 由此你能给出简便解法吗
分析:由三角形面积公式可知,只要利用距离公式求出
边AB的长和边AB上的高即可.
你还有其他解法吗
2.3.4两条平行直线间的距离
前面我们已经得到了两点间的距离公式、点到直线的距离公式.关于平面上的距离问题,两条平行直线间的距离也是值得研究的.
两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长.
分析:两条平行直线间的距离即为这两条平行直线中的一条直线上的一点到另一条直线的距离.
作业
P79 第10题
如图,以边BC的中点为原点,
边BC所在直线为x轴建立平面直角坐标系
(1)如图,在平面直角坐标系中,
点A,B, C的坐标分别为(1,0), (1, 1), (0, 1).
连接AB,BC. 设P(x,y)为正方形内一点,则O
