沪科版数学七年级上册 4.3《线段长短的比较》教学 课件(共21张ppt)
文档属性
| 名称 | 沪科版数学七年级上册 4.3《线段长短的比较》教学 课件(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 615.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
4.3 线段的长短比较
第四章 直线与角
沪科版
理解线段的和差关系,会用叠合与度量法比较线段 大小。
2.了解线段中点的概念和几何语言表示方法。
3.理解两点间距离的意义及“两点之间,线段最短” 的性质。
学习目标
导入新课
情境引入
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
你们平时是如何比较两个同学的身高的,说说看?
情境引入
1.53M,比你高3CM
1.50M
小明
小刚
合作探究
小明
小刚
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小刚
合作探究
比较两个同学高矮的方法总结:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
① 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
人可以抽象的看作是一条线段,你能从比较身高的方法中得到启示来比较两条线段的大小吗?
情境引入
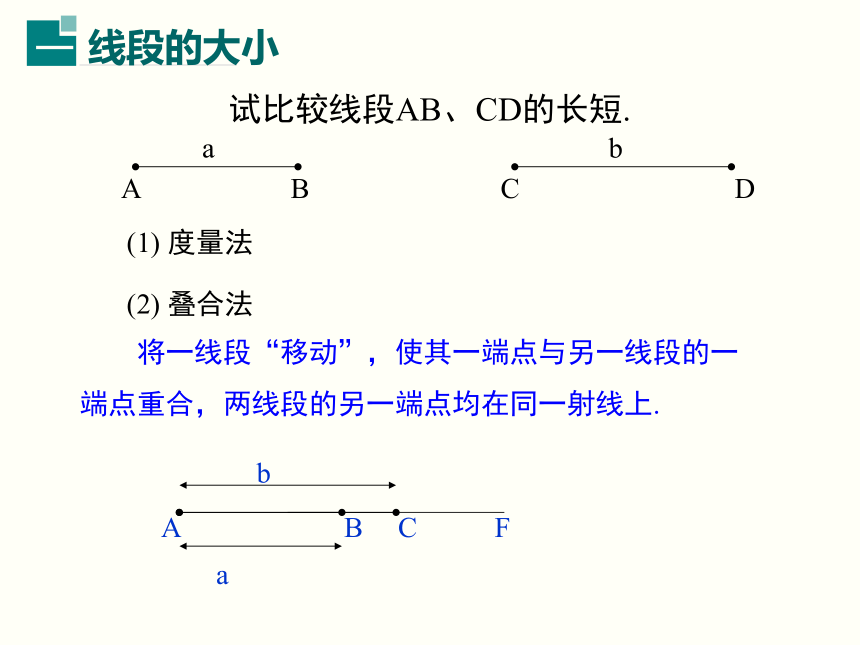
试比较线段AB、CD的长短.
(1) 度量法
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A
C
B
a
b
F
A B
C D
a
b
线段的大小
一
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
线段的和、差、倍、分
二
在直线上画出线段AB=a ,再在AB的延长线上画线段BC=b,线段AC就是 与 的和,记作AC= .如果在AB上画线段BD=b,那么线段AD就是 与 的差,记作AD= .
画一画
A
B
C
D
a
b
a
a+b
b
a-b
a+b
a-b
a
b
b
做一做
1.如图,C,D是线段AB上不同的两点,那么:
(1)AC=___ -DC, BD=___ - CD;
(2)AC=___ -BC, BD=___ -AD;
(3) AB= ___ + ____ + ____
A
C
D
B
AD
BC
AB
AB
AC
CD
DB
合作探究:问题3:
如图,已知点C在线段AB上,且AC=2cm,BC=2cm,试判断线段AC与BC的大小关系?点C为线段AB的什么点?
归纳:
1.线段的中点:把一条线段分成两条相等 线段的点,叫做这条线段的中点。
2.几何表示法:
●
●
●
A
C
B
或 AB=2AC=2CB
相等
中点
几何语言:∵M是线段AB的中点
∴AM=MB = AB
(或AB=2AM=2MB)
1
2
A
a
a
M
B
反过来:已知点A、B、M三点在同一直线上,且AM=MB
几何语言:∵AM=MB
∴M是线段AB的中点
M是线段AB的中点
加深认识线段中点几何语言(即书写)
例 已知:线段AB = 4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC 的中点.求DE的长
A B E C
D
解:∵D是线段AB的中点,AB=4
∵E是线段AC的中点,AC=11
典例精析
AD=DB= AB= X4= 2
AE=EC= AC= X11= 5.5
∴ DE=AE-AD= 5.5-2 = 3.5
有关线段的基本事实
三
议一议
甲
乙
如图:从甲地到乙地有四条道路,除它们外能否再修一条从甲地到乙地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线
结论:两点的所有连线中,线段最短.
简记:两点之间线段最短。
两点之间,线段最短
你能举出这条性质在生活中的应用吗?
1.如图,这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出. 你的理由是
B
A
.
2.把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?
变短了
(两点之间,线段最短)
1.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .
2.在一条笔直的公路两侧,分别有A、B两个村庄,如图,
现在要在公路l上建一个汽车站C,使汽车站到A、B两村庄
的距离之和最小,请在图中画出汽车站的位置.
C
B
练一练
>
>
>
两点之间线段最短
C
课堂小结
1.比较两条线段大小(长短)的方法:
度量法;
叠合法.
2.线段的中点
A M B
因为点M是线段AB的中点,所以 AM=BM= AB
(反过来说也是成立的);
3.两点之间的所有连线中,线段最短;
两点之间线段的长度 ,叫做这两点之间的距离.
●
●
●
必做题:P142 习题4.3
第2题,第4题。
选做题:同步练习
课后作业
4.3 线段的长短比较
第四章 直线与角
沪科版
理解线段的和差关系,会用叠合与度量法比较线段 大小。
2.了解线段中点的概念和几何语言表示方法。
3.理解两点间距离的意义及“两点之间,线段最短” 的性质。
学习目标
导入新课
情境引入
有一根长木棒,如何从它上面截下一段,使截下的木棒等于另一根短木棒的长?
你们平时是如何比较两个同学的身高的,说说看?
情境引入
1.53M,比你高3CM
1.50M
小明
小刚
合作探究
小明
小刚
我比你高!
你哪有我高啊!
服了吧!
喔,原来你比我高!
小明
小刚
合作探究
比较两个同学高矮的方法总结:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两
人的头顶,直接比出高矮;
① 用卷尺分别度量出两个同学的身高,将所得的
数值进行比较.
——度量法.
人可以抽象的看作是一条线段,你能从比较身高的方法中得到启示来比较两条线段的大小吗?
情境引入
试比较线段AB、CD的长短.
(1) 度量法
(2) 叠合法
将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上.
A
C
B
a
b
F
A B
C D
a
b
线段的大小
一
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
线段的和、差、倍、分
二
在直线上画出线段AB=a ,再在AB的延长线上画线段BC=b,线段AC就是 与 的和,记作AC= .如果在AB上画线段BD=b,那么线段AD就是 与 的差,记作AD= .
画一画
A
B
C
D
a
b
a
a+b
b
a-b
a+b
a-b
a
b
b
做一做
1.如图,C,D是线段AB上不同的两点,那么:
(1)AC=___ -DC, BD=___ - CD;
(2)AC=___ -BC, BD=___ -AD;
(3) AB= ___ + ____ + ____
A
C
D
B
AD
BC
AB
AB
AC
CD
DB
合作探究:问题3:
如图,已知点C在线段AB上,且AC=2cm,BC=2cm,试判断线段AC与BC的大小关系?点C为线段AB的什么点?
归纳:
1.线段的中点:把一条线段分成两条相等 线段的点,叫做这条线段的中点。
2.几何表示法:
●
●
●
A
C
B
或 AB=2AC=2CB
相等
中点
几何语言:∵M是线段AB的中点
∴AM=MB = AB
(或AB=2AM=2MB)
1
2
A
a
a
M
B
反过来:已知点A、B、M三点在同一直线上,且AM=MB
几何语言:∵AM=MB
∴M是线段AB的中点
M是线段AB的中点
加深认识线段中点几何语言(即书写)
例 已知:线段AB = 4,延长AB至点C,使AC=11.点D是AB的中点,点E是AC 的中点.求DE的长
A B E C
D
解:∵D是线段AB的中点,AB=4
∵E是线段AC的中点,AC=11
典例精析
AD=DB= AB= X4= 2
AE=EC= AC= X11= 5.5
∴ DE=AE-AD= 5.5-2 = 3.5
有关线段的基本事实
三
议一议
甲
乙
如图:从甲地到乙地有四条道路,除它们外能否再修一条从甲地到乙地的最短道路 如果能,请你联系以前所学的知识,在图上画出最短路线
结论:两点的所有连线中,线段最短.
简记:两点之间线段最短。
两点之间,线段最短
你能举出这条性质在生活中的应用吗?
1.如图,这是A、B两地之间的公路,在公路工程改造计划时,为使A、B两地行程最短,应如何设计线路?在图中画出. 你的理由是
B
A
.
2.把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?
变短了
(两点之间,线段最短)
1.如图,AB+BC AC,AC+BC AB,
AB+AC BC(填“>”“<”或“=”).
其中蕴含的数学道理是 .
2.在一条笔直的公路两侧,分别有A、B两个村庄,如图,
现在要在公路l上建一个汽车站C,使汽车站到A、B两村庄
的距离之和最小,请在图中画出汽车站的位置.
C
B
练一练
>
>
>
两点之间线段最短
C
课堂小结
1.比较两条线段大小(长短)的方法:
度量法;
叠合法.
2.线段的中点
A M B
因为点M是线段AB的中点,所以 AM=BM= AB
(反过来说也是成立的);
3.两点之间的所有连线中,线段最短;
两点之间线段的长度 ,叫做这两点之间的距离.
●
●
●
必做题:P142 习题4.3
第2题,第4题。
选做题:同步练习
课后作业
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
