沪科版数学七年级上册 3.5 三元一次方程组及其解法 课件(共21张PPT)
文档属性
| 名称 | 沪科版数学七年级上册 3.5 三元一次方程组及其解法 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
本节内容
3-5
三元一次方程组及其解法
沪科版七年级上册
情境引入
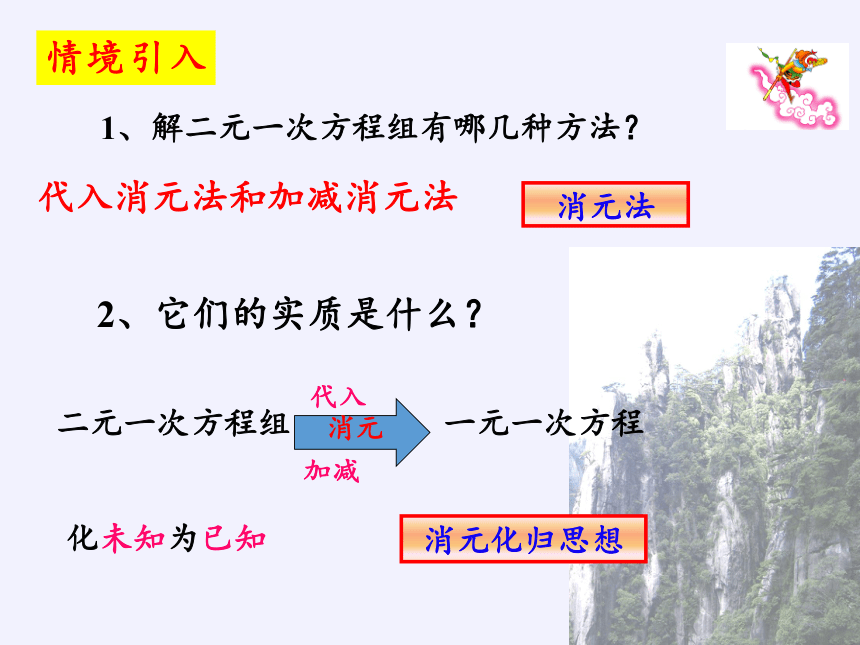
1、解二元一次方程组有哪几种方法?
2、它们的实质是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化未知为已知
消元化归思想
代入消元法和加减消元法
消元法
动脑筋
3.小丽家三口人的年龄之和为80岁,小丽的爸爸比妈妈大6岁,小丽的年龄是爸爸与妈妈年龄和的1/7. 试问这家人的年龄分别是多少岁?
可建立二元一次方程组来解决.
设爸爸的年龄为x岁,小丽的年龄为y岁,则妈妈的年龄为(x-6)岁. 根据题意得:
想一想,还有其他的方法列方程组求解吗?
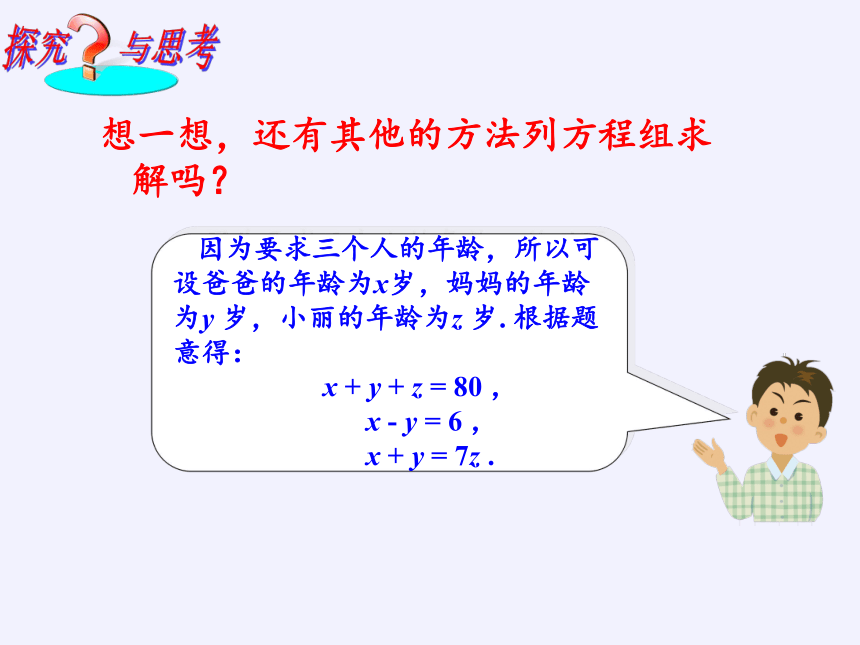
因为要求三个人的年龄,所以可设爸爸的年龄为x岁,妈妈的年龄为y 岁,小丽的年龄为z 岁. 根据题意得:
x + y + z = 80 ,
x - y = 6 ,
x + y = 7z .
探究 与思考
这种由三个一次方程组成的含三个未知数的方程组叫做三元一次方程组.
在三元一次方程组中,适合每一个方程的一组未知数的值,叫做这个方程组的解.
三人的年龄必须同时满足上述三个方程,所以,我们把这三个方程联立在一起写成:
结论
我国古代很早就开始对一次方程组进行研究,其中不少成果被收入古代数学著作《九章算术》中.《九章算术》的“方程”章,有许多关于一次方程组的内容.这一章的第一个问题译成现代汉语是这样的:
上等谷3束,中等谷2束,下等谷1束,共有39斗;
上等谷2束,中等谷3束,下等谷1束,共有34斗;
上等谷1束,中等谷2束,下等谷3束,共有26斗;
求上、中、下三等谷每束各是几斗?
注:斗是过去的容积计量单位.
不妨先用我们熟悉的数学符号来表述怎样解这个有3个未知数的问题.设上等谷每束x斗,中等谷每束y斗,下等谷每束z斗.
4.阅读“史话”,感受我国古代人民的智慧。
根据题意,得到一个三元一次方程组:
那么我国古代是怎么解决这个问题的呢?
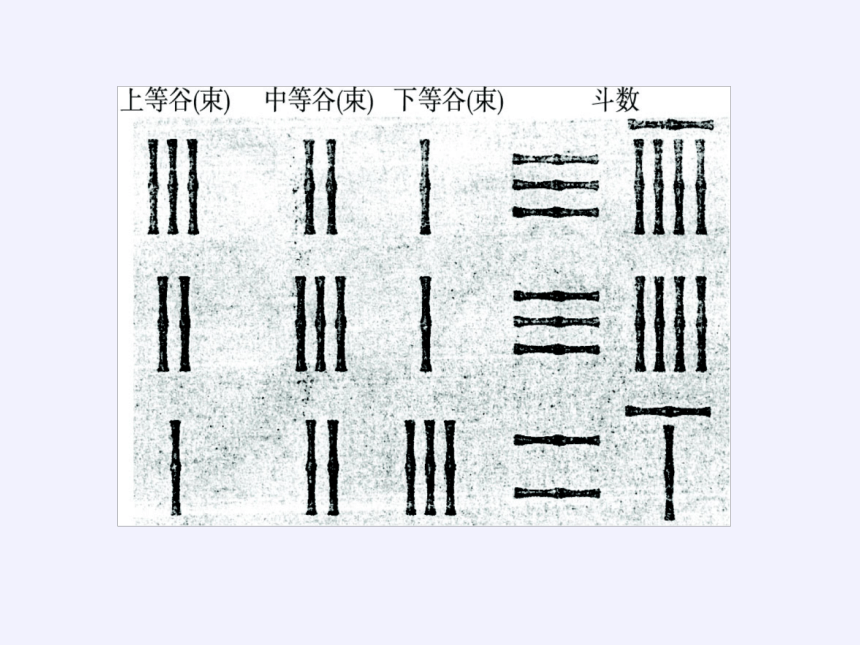
下面的算筹图代表了古代解决这个问题的方法,它是什么意思呢?
《九章算术》中的算筹图是竖排的.为看图方便,上图改为横排,使三个横行表示三句话的含义.
动脑筋
解二元一次方程组可以利用代入法或加减法消去一个未知数,使其转化为一元一次方程来求解.
那么我们在解三元一次方程组时,能不能同样利用代入法或加减法来消去一个或两个未知数,使其转化为二元一次方程组或一元一次方程呢?
例:解方程组:
解:①+②得到一个只含x和z的二元一次方程,
即2x + z = 86 .
再②+③,又得到一个只含x和z的二元一次方程,
即2x = 6 + 7z .
由此可得一个关于x,z的二元一次方程组
把x=38,z=10代入①式,得38 + y + 10 = 80 ,
解这个方程组,得
解得 y = 32 .
因此,三元一次方程组的解为
从上面解方程组的过程可以看出:
解三元一次方程组的基本思路是:消元
即:先消去一个未知数,将解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.
消元的基本方法仍然是代入法和加减法.
说一说
举
例
例 解三元一次方程组:
解: 先用加减消元法消去y:
①+②, 得 -x+3z =0 . ④
②×2+③, 得 -3x-2z =-11 . ⑤
解这个由④⑤联立成的二元一次方程组:
④×3-⑤,得 11z=11 ⑥
所以 z=1 ⑦
将⑦代入④,得 x = 3
将x , z的值代入① , 得 y = -2
①
②
③
所以,三元一次方程组的解为
í
ì
=
-
=
=
1
2
3
z
y
x
解三元一次方程组的基本思路是:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
错题分析
解方程组:
①
②
③
下面是小明同学解这个方程组的一部分过程:
①+②,得 3x+2z=13. ④
①+③,得 4x+3y=16. ⑤
解由④、⑤联立的方程组
师:小明的解法存在什么问题?
①+②消去的是y,①+③消去的是z,两次消元消去的不是同一个未知数,最后得到由④、⑤联立的方程组仍然是三元一次方程组。
解下列三元一次方程组:
巩固练习
解:①-③ , 得 y +z =0 . ④
④×2 -②, 得 z= - 6 .
所以原方程组的解为
把 z = -6代入②式, 得y = 6 .
把 y = 6代入①式, 得x = 1.
练习
解:①-②, 得 y -z =-3 .
①-③×2, 得 -2y-3z = 16 .
由此得到
把 y = -5,z = -2 代入③式, 得x = 8 .
解这个二元一次方程组得
所以原方程组的解为
当堂达标
1.解方程组:
(1)若先消去x,得到的含y,z的二元一次方程组是______.
(2)若先消去y,得到的含x,z的二元一次方程组是______.
(3)若先消去z,得到的含x,y的二元一次方程组是_______.
2. 选择一种你认为简便的消元方法求解上题的程组.
③×2-①,
③×3-②,得
②×2-①×3,
③×3-②,得
①+②,
①+③,得
①+②,
②-③,得
①×2+②×3,
③×3-①, 得
①×2+②×3,
②+③×2, 得
①
②
③
课堂小结
师:本节课主要学习了哪些内容 有什么收获
教师总结:
本节课主要学习了三元一次方程的概念,以及用加减消元和代入消元法解简单的三元一次方程组.体现了化“复杂”为“简单”、化“未知”为“已知”的消元化归思想,并且两次消元只有消去同一个未知数才能达到化“三元”为“二元”的目的.求出方程组的解之后,还必须代入原方程组进行口头检验,保证解的正确性.
布置作业
1、课堂作业
P118习题第1题(1)、(2)
2、课外作业
P116练习第1题
基础训练3.5(1)
3、预习p116例2,对于稍复杂三元一次
方程组的解法
谢 谢
本节内容
3-5
三元一次方程组及其解法
沪科版七年级上册
情境引入
1、解二元一次方程组有哪几种方法?
2、它们的实质是什么?
二元一次方程组
代入
加减
消元
一元一次方程
化未知为已知
消元化归思想
代入消元法和加减消元法
消元法
动脑筋
3.小丽家三口人的年龄之和为80岁,小丽的爸爸比妈妈大6岁,小丽的年龄是爸爸与妈妈年龄和的1/7. 试问这家人的年龄分别是多少岁?
可建立二元一次方程组来解决.
设爸爸的年龄为x岁,小丽的年龄为y岁,则妈妈的年龄为(x-6)岁. 根据题意得:
想一想,还有其他的方法列方程组求解吗?
因为要求三个人的年龄,所以可设爸爸的年龄为x岁,妈妈的年龄为y 岁,小丽的年龄为z 岁. 根据题意得:
x + y + z = 80 ,
x - y = 6 ,
x + y = 7z .
探究 与思考
这种由三个一次方程组成的含三个未知数的方程组叫做三元一次方程组.
在三元一次方程组中,适合每一个方程的一组未知数的值,叫做这个方程组的解.
三人的年龄必须同时满足上述三个方程,所以,我们把这三个方程联立在一起写成:
结论
我国古代很早就开始对一次方程组进行研究,其中不少成果被收入古代数学著作《九章算术》中.《九章算术》的“方程”章,有许多关于一次方程组的内容.这一章的第一个问题译成现代汉语是这样的:
上等谷3束,中等谷2束,下等谷1束,共有39斗;
上等谷2束,中等谷3束,下等谷1束,共有34斗;
上等谷1束,中等谷2束,下等谷3束,共有26斗;
求上、中、下三等谷每束各是几斗?
注:斗是过去的容积计量单位.
不妨先用我们熟悉的数学符号来表述怎样解这个有3个未知数的问题.设上等谷每束x斗,中等谷每束y斗,下等谷每束z斗.
4.阅读“史话”,感受我国古代人民的智慧。
根据题意,得到一个三元一次方程组:
那么我国古代是怎么解决这个问题的呢?
下面的算筹图代表了古代解决这个问题的方法,它是什么意思呢?
《九章算术》中的算筹图是竖排的.为看图方便,上图改为横排,使三个横行表示三句话的含义.
动脑筋
解二元一次方程组可以利用代入法或加减法消去一个未知数,使其转化为一元一次方程来求解.
那么我们在解三元一次方程组时,能不能同样利用代入法或加减法来消去一个或两个未知数,使其转化为二元一次方程组或一元一次方程呢?
例:解方程组:
解:①+②得到一个只含x和z的二元一次方程,
即2x + z = 86 .
再②+③,又得到一个只含x和z的二元一次方程,
即2x = 6 + 7z .
由此可得一个关于x,z的二元一次方程组
把x=38,z=10代入①式,得38 + y + 10 = 80 ,
解这个方程组,得
解得 y = 32 .
因此,三元一次方程组的解为
从上面解方程组的过程可以看出:
解三元一次方程组的基本思路是:消元
即:先消去一个未知数,将解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程.
消元的基本方法仍然是代入法和加减法.
说一说
举
例
例 解三元一次方程组:
解: 先用加减消元法消去y:
①+②, 得 -x+3z =0 . ④
②×2+③, 得 -3x-2z =-11 . ⑤
解这个由④⑤联立成的二元一次方程组:
④×3-⑤,得 11z=11 ⑥
所以 z=1 ⑦
将⑦代入④,得 x = 3
将x , z的值代入① , 得 y = -2
①
②
③
所以,三元一次方程组的解为
í
ì
=
-
=
=
1
2
3
z
y
x
解三元一次方程组的基本思路是:通过“代入”或“加减”进行消元,把“三元”转化为“二元”,使解三元一次方程组转化为解二元一次方程组,进而再转化为解一元一次方程。
错题分析
解方程组:
①
②
③
下面是小明同学解这个方程组的一部分过程:
①+②,得 3x+2z=13. ④
①+③,得 4x+3y=16. ⑤
解由④、⑤联立的方程组
师:小明的解法存在什么问题?
①+②消去的是y,①+③消去的是z,两次消元消去的不是同一个未知数,最后得到由④、⑤联立的方程组仍然是三元一次方程组。
解下列三元一次方程组:
巩固练习
解:①-③ , 得 y +z =0 . ④
④×2 -②, 得 z= - 6 .
所以原方程组的解为
把 z = -6代入②式, 得y = 6 .
把 y = 6代入①式, 得x = 1.
练习
解:①-②, 得 y -z =-3 .
①-③×2, 得 -2y-3z = 16 .
由此得到
把 y = -5,z = -2 代入③式, 得x = 8 .
解这个二元一次方程组得
所以原方程组的解为
当堂达标
1.解方程组:
(1)若先消去x,得到的含y,z的二元一次方程组是______.
(2)若先消去y,得到的含x,z的二元一次方程组是______.
(3)若先消去z,得到的含x,y的二元一次方程组是_______.
2. 选择一种你认为简便的消元方法求解上题的程组.
③×2-①,
③×3-②,得
②×2-①×3,
③×3-②,得
①+②,
①+③,得
①+②,
②-③,得
①×2+②×3,
③×3-①, 得
①×2+②×3,
②+③×2, 得
①
②
③
课堂小结
师:本节课主要学习了哪些内容 有什么收获
教师总结:
本节课主要学习了三元一次方程的概念,以及用加减消元和代入消元法解简单的三元一次方程组.体现了化“复杂”为“简单”、化“未知”为“已知”的消元化归思想,并且两次消元只有消去同一个未知数才能达到化“三元”为“二元”的目的.求出方程组的解之后,还必须代入原方程组进行口头检验,保证解的正确性.
布置作业
1、课堂作业
P118习题第1题(1)、(2)
2、课外作业
P116练习第1题
基础训练3.5(1)
3、预习p116例2,对于稍复杂三元一次
方程组的解法
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
