2021-2022学年高中数学人教版A版(2019)选择性必修一2.5.1直线与圆的位置关系 课件(共33张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一2.5.1直线与圆的位置关系 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:01:41 | ||
图片预览







文档简介
(共33张PPT)
2.5.1 直线与圆的位置关系
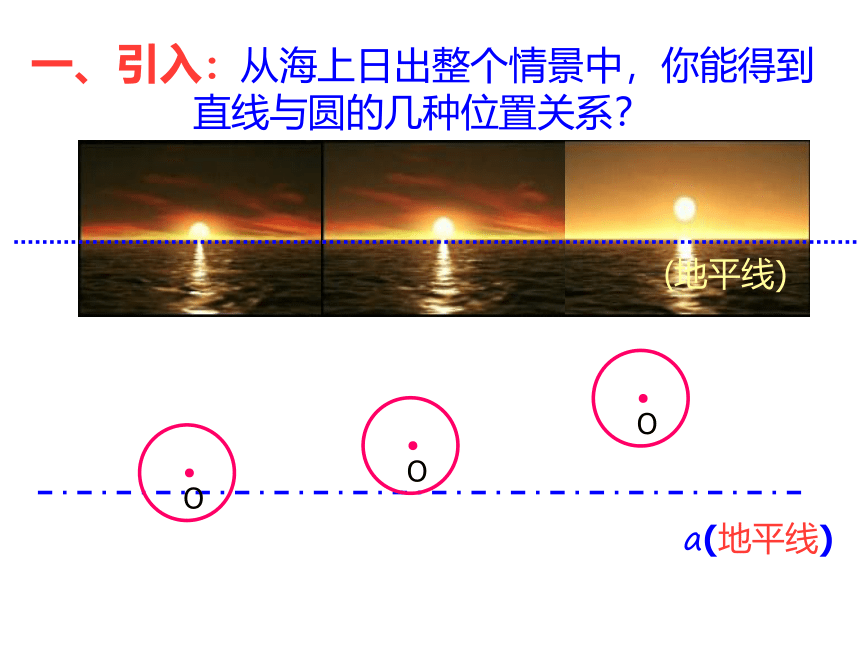
(地平线)
a(地平线)
●O
●O
●O
一、引入:从海上日出整个情景中,你能得到直线与圆的几种位置关系?
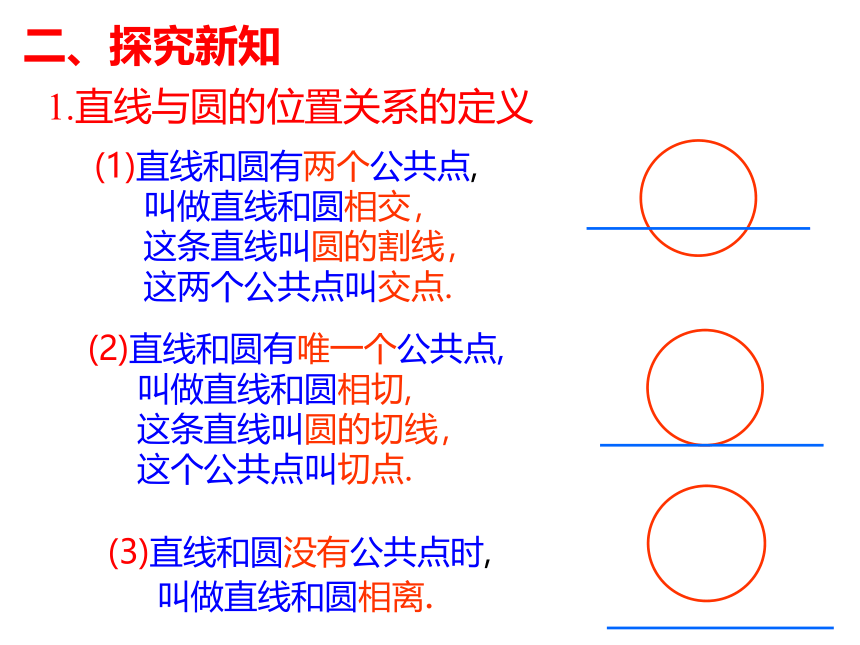
(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点.
(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点.
(3)直线和圆没有公共点时,
叫做直线和圆相离.
1.直线与圆的位置关系的定义
二、探究新知
相交
相切
相离
上述变化过程中,除了交点个数发生了变化,还有什么量在改变?你能否用利用这种变化关系来判定直线与圆的位置关系?
2.探究:直线与圆的位置关系的判定
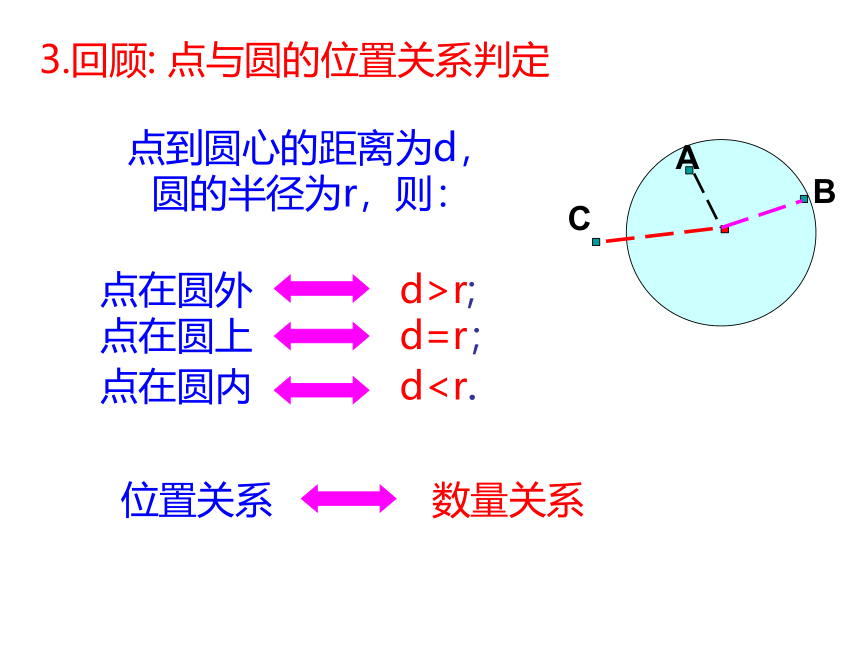
点到圆心的距离为d, 圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 dA
B
C
位置关系
数量关系
3.回顾: 点与圆的位置关系判定
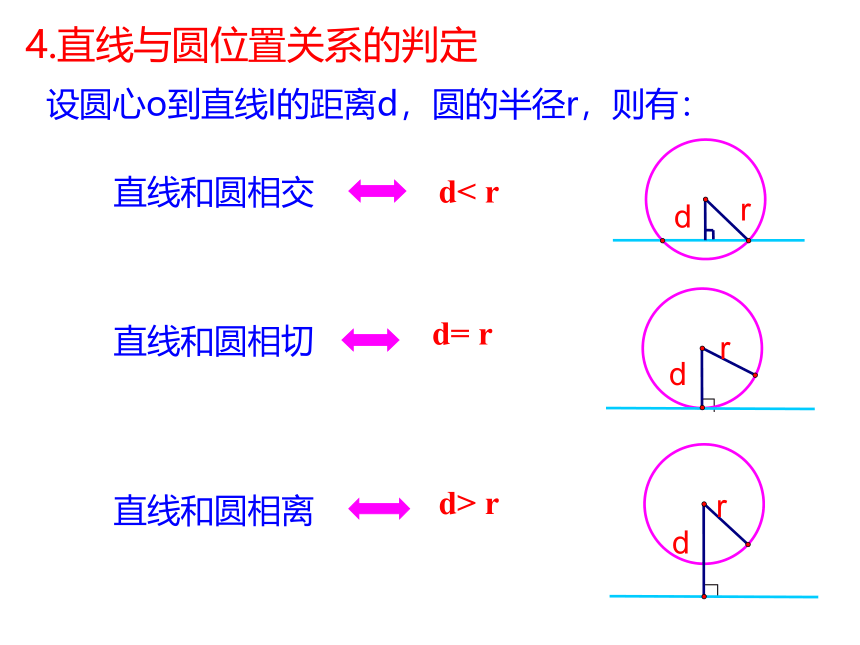
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
4.直线与圆位置关系的判定
设圆心o到直线l的距离d,圆的半径r,则有:
1.从几何角度判断,定性描述
2.利用方程计算,定量判断
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 ,
的个数来判断;(代数法)
(2)根据性质,由 , 的关系来判断。(几何法)
两
直线与圆的公共点
圆心到直线的距离d与半径r
1.已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交,则 .
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
2
1
0
三、巩固新知
解法1:
3x+y-6=0 ①
x2+y2-2y-4=0 ②
消去y得:
x2-3x+2=0
解得: x1=1, x2=2
∴直线l与圆C的两个交点是A(2,0),B(1,3).
解方程组:
①
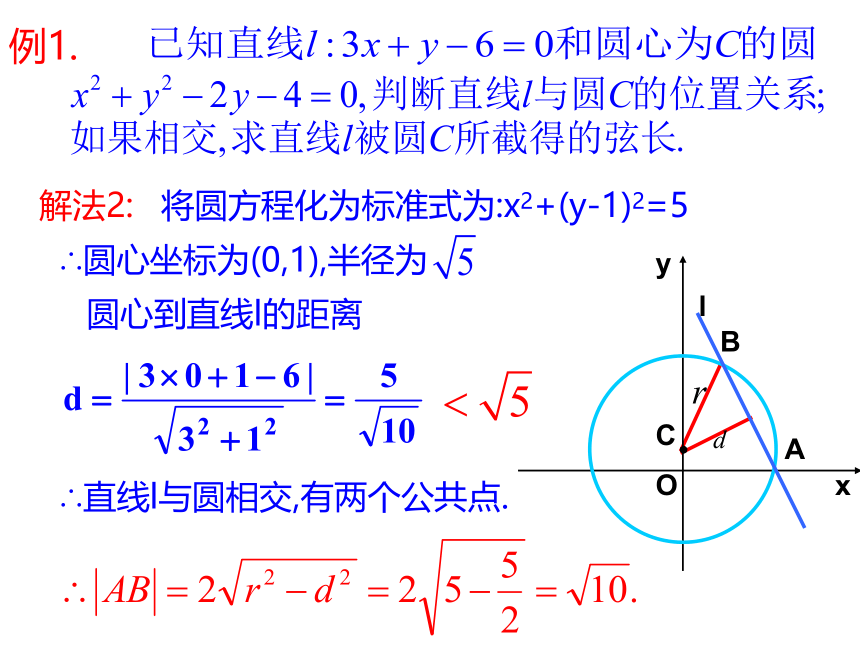
例1.
解法2:
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
例1.
.
x
y
O
C
A
B
l
代数法:操作步骤
1).将直线方程与圆的方程联立成方程组;
2).通过消元,得到一个一元二次方程;
3).求出其判别式△的值;
4).比较△与0的大小关系:
若△>0,则直线与圆相交;
若△=0,则直线与圆相切;
若△<0,则直线与圆相离.
4.判定方法的总结
1).把直线方程化为一般式Ax+By+C=0 ,并由圆的方程
求出圆心坐标和半径r;
2).利用点到直线的距离公式求圆心到直线的距离d;
若d>r,则直线与圆相离;
若d=r,则直线与圆相切;
若d<r,则直线与圆相交.
3).比较d与r的大小关系:
几何法:操作步骤
4.判定方法的总结
适当利用几何图形,几何性质,有助于简化运算
“数形结合”的思想
只要有相切;就要考虑圆心到切点的直线!
O
A
|OA|=r(即:d=r)
kl·kOA=-1
5.直线与圆相切
x=2
例2.
例2.
x=2
设点M(x0,y0)为圆 x2+y2=r2上一点,则过M点可以作几条圆的切线?如何求过点M的圆的切线方程?
x
o
y
x0x+y0y=r2
M(x0,y0)
7.直线与圆相切---圆的切线方程
4).以C(1,3)为圆心,并和直线3x-4y-6=0相切的圆的
方程是 .
1).直线3x+4y-2=0与圆x2+y2-2x=0的位置关系 .
(x-1)2+(y-3)2=9
相交
2).直线y=x+6,圆x2+y2-2y-4=0的位置关系是 .
相离
3).若直线x-y=2与圆(x-a)2+y2=4的圆心的距离为 ,
则实数a的值为 .
0或4
8.变式训练
点O是圆拱所在圆的圆心吗?
思考
如果不建立平面直角坐标系,你能解决这个问题吗?由此比较综合法和坐标法的特点.
综合法,需要添加多条辅助线,有一定技巧,并多次
使用勾股定理,过程比较复杂。
例题4:一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为20km的圆形区域。已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处。如果轮船沿直线返港,那么它是否会有触礁的危险?
x
O
y
分析:为解决这个问题,我们以小岛中心为原点 O,东西方向为 x 轴,建立如图所示的直角坐标系,其中取 10km 为单位长度.
.
港口
.
轮船
小岛
.
.
x
轮船航线所在直线 l 的方程为:
问题归结为圆心为O的 圆与直线l有无公共点.
解:这样,受暗礁影响的圆形区域所对应的圆心
为O的圆的方程为:
O
y
港口
.
轮船
(4,0)
(0,3)
(2,0)
11.用坐标法解决问题的步骤
——“三步曲”
1).建立适当的平面直角坐标系,用坐标和方程表示问
题中的几何元素,将平面几何问题转化为代数问题。
2).通过代数运算,解决代数问题(有目的地).
3).把代数运算结果“翻译”成几何结论.
几何
代数
几何
点、线、面等几何要素用向量进行表示
2.向量运算给向量表示几何要素带来便利性
(数乘,加法,减法,基底等)
3.向量在刻画长度和角度有着强大的功效。
已知内接于圆的四边形的对角线互相垂直,
求证圆心到一边的距离等于这条边所对边长的一半
分析:将自然语言转化为图形语言,建立适当的直角坐标系证明问题。由已知,可选择互相垂直的两条对角线所在的直线为坐标轴,关键在求圆心坐标
12.变式训练
证明:以AC为x轴,BD为y轴建立直角坐标系.
则四个顶点坐标分别为
A(a,0),B(0,b),C(0,c),D(0,d)
因此,圆心到一条边的距离等于等于这条边所对边长一半。
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
第一步:建立坐标系,用坐标表示有关的量,
自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,其反射光线所在的直线与圆 x2+y2-4x-4y+7=0相切,求反射光线所在直线的方程
l : 4x+3y+3=0或3x+4y-3=0
13.变式训练
反射光线所在的直线为
4x﹣3y+3=0 或3x﹣4y﹣3=0 .
(2)光线自A到切点所经过的路程.
根据光线的对称性,A(﹣3,3)关于x轴的对称点为B(﹣3,﹣3),
光线从A点到切点所经过的路程等于B点到切点所经过的路程,(7 )
14.变式:求与圆C:x2+y2﹣x+2y=0,关于
直线L:x﹣y+1=0对称的圆的方程.
解决问题的关键在于会求点关于直线的
对称点的坐标,主要利用两个结论:
①两点的连线和已知直线垂直;
②两点的中点在已知直线上.
解:圆x2+y2﹣x+2y=0转化为标准方程为:
1.直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
五、课堂小结
2.判定直线与圆的位置关系的方法有____种:
两
(1)根据定义,由 ,
的个数来判断;(代数法)
直线与圆的公共点
(2)根据性质,由 , 的关系来判断。(几何法)
圆心到直线的距离d与半径r
(3)在实际应用中,________常用几何法,
________常用代数法。
做判断
求交点
作业: 课本P98 习题2.5 2 题
2.5.1 直线与圆的位置关系
(地平线)
a(地平线)
●O
●O
●O
一、引入:从海上日出整个情景中,你能得到直线与圆的几种位置关系?
(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点.
(1)直线和圆有两个公共点,
叫做直线和圆相交,
这条直线叫圆的割线,
这两个公共点叫交点.
(3)直线和圆没有公共点时,
叫做直线和圆相离.
1.直线与圆的位置关系的定义
二、探究新知
相交
相切
相离
上述变化过程中,除了交点个数发生了变化,还有什么量在改变?你能否用利用这种变化关系来判定直线与圆的位置关系?
2.探究:直线与圆的位置关系的判定
点到圆心的距离为d, 圆的半径为r,则:
点在圆外 d>r;
点在圆上 d=r;
点在圆内 d
B
C
位置关系
数量关系
3.回顾: 点与圆的位置关系判定
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
4.直线与圆位置关系的判定
设圆心o到直线l的距离d,圆的半径r,则有:
1.从几何角度判断,定性描述
2.利用方程计算,定量判断
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由 ,
的个数来判断;(代数法)
(2)根据性质,由 , 的关系来判断。(几何法)
两
直线与圆的公共点
圆心到直线的距离d与半径r
1.已知圆的直径为13cm,设直线和圆心的距离为d :
3)若d= 8 cm ,则直线与圆______, 直线与圆有____个公共点.
2)若d=6.5cm ,则直线与圆______, 直线与圆有____个公共点.
1)若d=4.5cm ,则直线与圆 , 直线与圆有____个公共点.
2.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
3)若AB和⊙O相交,则 .
相交
相切
相离
d > 5cm
d = 5cm
d < 5cm
2
1
0
三、巩固新知
解法1:
3x+y-6=0 ①
x2+y2-2y-4=0 ②
消去y得:
x2-3x+2=0
解得: x1=1, x2=2
∴直线l与圆C的两个交点是A(2,0),B(1,3).
解方程组:
①
例1.
解法2:
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
例1.
.
x
y
O
C
A
B
l
代数法:操作步骤
1).将直线方程与圆的方程联立成方程组;
2).通过消元,得到一个一元二次方程;
3).求出其判别式△的值;
4).比较△与0的大小关系:
若△>0,则直线与圆相交;
若△=0,则直线与圆相切;
若△<0,则直线与圆相离.
4.判定方法的总结
1).把直线方程化为一般式Ax+By+C=0 ,并由圆的方程
求出圆心坐标和半径r;
2).利用点到直线的距离公式求圆心到直线的距离d;
若d>r,则直线与圆相离;
若d=r,则直线与圆相切;
若d<r,则直线与圆相交.
3).比较d与r的大小关系:
几何法:操作步骤
4.判定方法的总结
适当利用几何图形,几何性质,有助于简化运算
“数形结合”的思想
只要有相切;就要考虑圆心到切点的直线!
O
A
|OA|=r(即:d=r)
kl·kOA=-1
5.直线与圆相切
x=2
例2.
例2.
x=2
设点M(x0,y0)为圆 x2+y2=r2上一点,则过M点可以作几条圆的切线?如何求过点M的圆的切线方程?
x
o
y
x0x+y0y=r2
M(x0,y0)
7.直线与圆相切---圆的切线方程
4).以C(1,3)为圆心,并和直线3x-4y-6=0相切的圆的
方程是 .
1).直线3x+4y-2=0与圆x2+y2-2x=0的位置关系 .
(x-1)2+(y-3)2=9
相交
2).直线y=x+6,圆x2+y2-2y-4=0的位置关系是 .
相离
3).若直线x-y=2与圆(x-a)2+y2=4的圆心的距离为 ,
则实数a的值为 .
0或4
8.变式训练
点O是圆拱所在圆的圆心吗?
思考
如果不建立平面直角坐标系,你能解决这个问题吗?由此比较综合法和坐标法的特点.
综合法,需要添加多条辅助线,有一定技巧,并多次
使用勾股定理,过程比较复杂。
例题4:一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为20km的圆形区域。已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处。如果轮船沿直线返港,那么它是否会有触礁的危险?
x
O
y
分析:为解决这个问题,我们以小岛中心为原点 O,东西方向为 x 轴,建立如图所示的直角坐标系,其中取 10km 为单位长度.
.
港口
.
轮船
小岛
.
.
x
轮船航线所在直线 l 的方程为:
问题归结为圆心为O的 圆与直线l有无公共点.
解:这样,受暗礁影响的圆形区域所对应的圆心
为O的圆的方程为:
O
y
港口
.
轮船
(4,0)
(0,3)
(2,0)
11.用坐标法解决问题的步骤
——“三步曲”
1).建立适当的平面直角坐标系,用坐标和方程表示问
题中的几何元素,将平面几何问题转化为代数问题。
2).通过代数运算,解决代数问题(有目的地).
3).把代数运算结果“翻译”成几何结论.
几何
代数
几何
点、线、面等几何要素用向量进行表示
2.向量运算给向量表示几何要素带来便利性
(数乘,加法,减法,基底等)
3.向量在刻画长度和角度有着强大的功效。
已知内接于圆的四边形的对角线互相垂直,
求证圆心到一边的距离等于这条边所对边长的一半
分析:将自然语言转化为图形语言,建立适当的直角坐标系证明问题。由已知,可选择互相垂直的两条对角线所在的直线为坐标轴,关键在求圆心坐标
12.变式训练
证明:以AC为x轴,BD为y轴建立直角坐标系.
则四个顶点坐标分别为
A(a,0),B(0,b),C(0,c),D(0,d)
因此,圆心到一条边的距离等于等于这条边所对边长一半。
第二步:进行有关代数运算
第三步:把代数运算结果翻译成几何关系.
第一步:建立坐标系,用坐标表示有关的量,
自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,其反射光线所在的直线与圆 x2+y2-4x-4y+7=0相切,求反射光线所在直线的方程
l : 4x+3y+3=0或3x+4y-3=0
13.变式训练
反射光线所在的直线为
4x﹣3y+3=0 或3x﹣4y﹣3=0 .
(2)光线自A到切点所经过的路程.
根据光线的对称性,A(﹣3,3)关于x轴的对称点为B(﹣3,﹣3),
光线从A点到切点所经过的路程等于B点到切点所经过的路程,(7 )
14.变式:求与圆C:x2+y2﹣x+2y=0,关于
直线L:x﹣y+1=0对称的圆的方程.
解决问题的关键在于会求点关于直线的
对称点的坐标,主要利用两个结论:
①两点的连线和已知直线垂直;
②两点的中点在已知直线上.
解:圆x2+y2﹣x+2y=0转化为标准方程为:
1.直线与圆的位置关系:
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
五、课堂小结
2.判定直线与圆的位置关系的方法有____种:
两
(1)根据定义,由 ,
的个数来判断;(代数法)
直线与圆的公共点
(2)根据性质,由 , 的关系来判断。(几何法)
圆心到直线的距离d与半径r
(3)在实际应用中,________常用几何法,
________常用代数法。
做判断
求交点
作业: 课本P98 习题2.5 2 题
