2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.1椭圆及其标准方程 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.1椭圆及其标准方程 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 503.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
3.1.1 椭圆及其标准方程
引例:
若取一条长度一定且没有弹性的细绳,把它的两端
都固定在图板的同一点处,套上铅笔,拉紧绳子,移动
笔尖,这时笔尖画出的轨迹是什么图形?
结论: 平面内到一个定点的距离等于定长的
点的轨迹是圆.
思考:平面内到两定点
的距离之和等于定长
的点的轨迹又是什么?
结论:平面内到两个定点的距离等于定长的点的轨迹是
椭圆.
若将细绳的两端拉开一段距离,分别固定在图板上
不同的两点F1、F2处,并用笔尖拉紧绳子,再移动笔尖
一周,这时笔尖画出的轨迹是什么图形呢?
探究1:
若细绳长不变, 两定点的距离逐步拉大,则该轨迹
有何变化?
探究2:
结论:平面内到两个定点的距离等于定长的点的轨迹是
椭圆.
若将细绳的两端拉开一段距离,分别固定在图板上
不同的两点F1、F2处,并用笔尖拉紧绳子,再移动笔尖
一周,这时笔尖画出的轨迹是什么图形呢?
探究1:
若细绳长不变, 两定点的距离逐步拉大,则该轨迹
有何变化?
探究2:
结论:绳长记为2a,两定点间的距离记为2c(c≠0).
(1)当2a>2c时,轨迹是 ;
(2)当2a=2c时,轨迹是 ;
(3)当2a<2c时, ;
椭圆
以F1、 F2为端点的线段
无轨迹
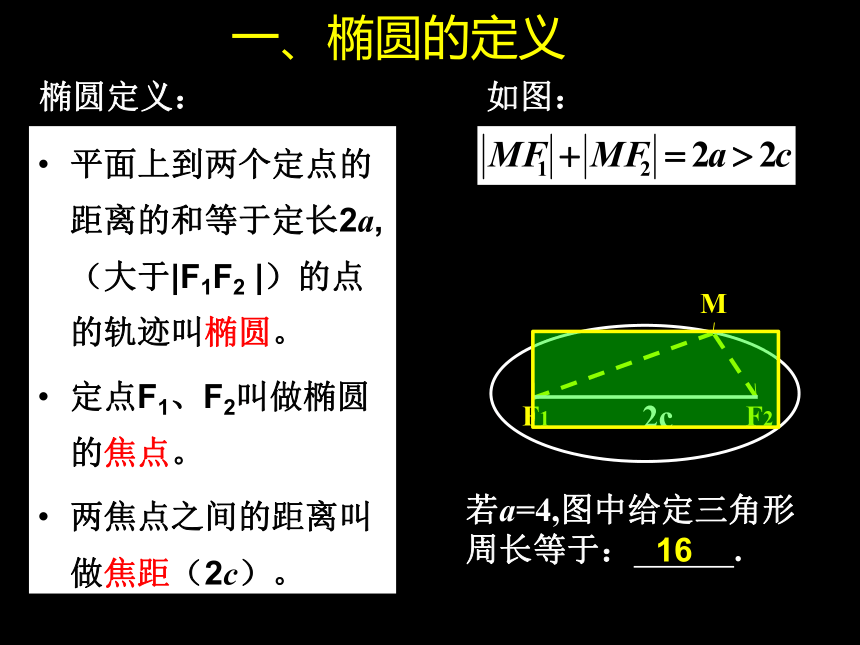
平面上到两个定点的距离的和等于定长2a,(大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。
椭圆定义:
如图:
一、椭圆的定义
F1
F2
M
2c
若a=4,图中给定三角形周长等于: .
16
O
x
y
F1
F2
M
如图所示:F1、F2为两定点,且
|F1F2|=2c,求平面内到两定点
F1、F2距离之和为定值2a(2a>2c)
的动点M的轨迹方程。
解:以F1F2所在直线为x轴,线段F1F2的垂直平分线为y轴
建立直角坐标系,
(-c,0)
(c,0)
(x,y)
设M(x,y)为所求轨迹上的任意一点,
则椭圆就是集合P={M||MF1|+ |MF2|=2a}
如何化简
则焦点F1、F2的坐标分别为(-c,0)、(c,0)。
问题: 求曲线方程的基本步骤?
(1)建系设点;
(2)写出条件;
(3)列出方程;
(4)化简方程;
(5)下结论。
O
x
y
F1
F2
M
(-c,0)
(c,0)
(x,y)
整理,得 (a2-c2)x2+a2y2=a2(a2-c2)
∵2a>2c>0,即a>c>0,∴a2-c2>0,
(a>b>0)
两边同除以a2(a2-c2)得:
P
那么①式
如图点P是椭圆与y轴正半轴的交点
①
你能在图中找出
表示a,c, ,
的线段吗?
O
x
y
F1
F2
M
O
x
y
F1
F2
M
椭圆的标准方程
-a
例题:
1.已知椭圆方程为 ,
则(1)a= , b= , c= ;
(2)焦点在 轴上,其焦点坐标为 ,
焦距为 。
(3)若椭圆方程为 ,
其焦点坐标为 .
5
4
3
(-3,0)、(3,0)
6
x
(0,3)、(0,-3)
(4)已知椭圆上一点 P到左焦点F1的距离等于6,
则点P到右焦点的距离是 ;
(5)若CD为过左焦点F1的弦,
则 CF1F2的周长为 ,
F2CD的周长为 。
1.已知椭圆方程为 ,
F1
F2
C
D
4
16
20
O
x
y
2.(课本例1)已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 , 求它的标准方程.
解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知
所以
又因为 ,所以
因此, 所求椭圆的标准方程为
2.(课本例1)已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 , 求它的标准方程.
解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为
①
②
联立①②,
因此, 所求椭圆的标准方程为
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.
巩固练习
1、动点P到两定点F1(-4,0),F2(4,0)的距离和是7,则
动点P的轨迹为( )
变式:
(1)动点P到两定点F1(-4,0),F2(4,0)的距离和是8,则
动点P的轨迹为( )
(2)动点P到两定点F1(-4,0),F2(4,0)的距离和是9,则
动点P的轨迹为( )
A.椭圆 B.线段F1F2 C.直线F1F2 D.无轨迹
D
B
A
小结:
(1)椭圆的定义
平面上到两个定点的距离的和等于定长2a
(大于2c)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。
(2)椭圆的两种标准方程
y
o
F1
F2
M
x
y
x
o
F2
F1
M
定 义
图 形
标准方程
焦点及位置
判定
a,b,c之间的关系
|MF1|+|MF2|=2a
作业:
P109 2
3.1.1 椭圆及其标准方程
引例:
若取一条长度一定且没有弹性的细绳,把它的两端
都固定在图板的同一点处,套上铅笔,拉紧绳子,移动
笔尖,这时笔尖画出的轨迹是什么图形?
结论: 平面内到一个定点的距离等于定长的
点的轨迹是圆.
思考:平面内到两定点
的距离之和等于定长
的点的轨迹又是什么?
结论:平面内到两个定点的距离等于定长的点的轨迹是
椭圆.
若将细绳的两端拉开一段距离,分别固定在图板上
不同的两点F1、F2处,并用笔尖拉紧绳子,再移动笔尖
一周,这时笔尖画出的轨迹是什么图形呢?
探究1:
若细绳长不变, 两定点的距离逐步拉大,则该轨迹
有何变化?
探究2:
结论:平面内到两个定点的距离等于定长的点的轨迹是
椭圆.
若将细绳的两端拉开一段距离,分别固定在图板上
不同的两点F1、F2处,并用笔尖拉紧绳子,再移动笔尖
一周,这时笔尖画出的轨迹是什么图形呢?
探究1:
若细绳长不变, 两定点的距离逐步拉大,则该轨迹
有何变化?
探究2:
结论:绳长记为2a,两定点间的距离记为2c(c≠0).
(1)当2a>2c时,轨迹是 ;
(2)当2a=2c时,轨迹是 ;
(3)当2a<2c时, ;
椭圆
以F1、 F2为端点的线段
无轨迹
平面上到两个定点的距离的和等于定长2a,(大于|F1F2 |)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。
椭圆定义:
如图:
一、椭圆的定义
F1
F2
M
2c
若a=4,图中给定三角形周长等于: .
16
O
x
y
F1
F2
M
如图所示:F1、F2为两定点,且
|F1F2|=2c,求平面内到两定点
F1、F2距离之和为定值2a(2a>2c)
的动点M的轨迹方程。
解:以F1F2所在直线为x轴,线段F1F2的垂直平分线为y轴
建立直角坐标系,
(-c,0)
(c,0)
(x,y)
设M(x,y)为所求轨迹上的任意一点,
则椭圆就是集合P={M||MF1|+ |MF2|=2a}
如何化简
则焦点F1、F2的坐标分别为(-c,0)、(c,0)。
问题: 求曲线方程的基本步骤?
(1)建系设点;
(2)写出条件;
(3)列出方程;
(4)化简方程;
(5)下结论。
O
x
y
F1
F2
M
(-c,0)
(c,0)
(x,y)
整理,得 (a2-c2)x2+a2y2=a2(a2-c2)
∵2a>2c>0,即a>c>0,∴a2-c2>0,
(a>b>0)
两边同除以a2(a2-c2)得:
P
那么①式
如图点P是椭圆与y轴正半轴的交点
①
你能在图中找出
表示a,c, ,
的线段吗?
O
x
y
F1
F2
M
O
x
y
F1
F2
M
椭圆的标准方程
-a
例题:
1.已知椭圆方程为 ,
则(1)a= , b= , c= ;
(2)焦点在 轴上,其焦点坐标为 ,
焦距为 。
(3)若椭圆方程为 ,
其焦点坐标为 .
5
4
3
(-3,0)、(3,0)
6
x
(0,3)、(0,-3)
(4)已知椭圆上一点 P到左焦点F1的距离等于6,
则点P到右焦点的距离是 ;
(5)若CD为过左焦点F1的弦,
则 CF1F2的周长为 ,
F2CD的周长为 。
1.已知椭圆方程为 ,
F1
F2
C
D
4
16
20
O
x
y
2.(课本例1)已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 , 求它的标准方程.
解法一:因为椭圆的焦点在x轴上,所以设它的标准方程为
由椭圆的定义知
所以
又因为 ,所以
因此, 所求椭圆的标准方程为
2.(课本例1)已知椭圆的两个焦点坐标分别是(-2,0),
(2,0), 并且经过点 , 求它的标准方程.
解法二:因为椭圆的焦点在x轴上,所以设它的标准方程为
①
②
联立①②,
因此, 所求椭圆的标准方程为
求椭圆标准方程的解题步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用待定系数法确定a、b的值,
写出椭圆的标准方程.
巩固练习
1、动点P到两定点F1(-4,0),F2(4,0)的距离和是7,则
动点P的轨迹为( )
变式:
(1)动点P到两定点F1(-4,0),F2(4,0)的距离和是8,则
动点P的轨迹为( )
(2)动点P到两定点F1(-4,0),F2(4,0)的距离和是9,则
动点P的轨迹为( )
A.椭圆 B.线段F1F2 C.直线F1F2 D.无轨迹
D
B
A
小结:
(1)椭圆的定义
平面上到两个定点的距离的和等于定长2a
(大于2c)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)。
(2)椭圆的两种标准方程
y
o
F1
F2
M
x
y
x
o
F2
F1
M
定 义
图 形
标准方程
焦点及位置
判定
a,b,c之间的关系
|MF1|+|MF2|=2a
作业:
P109 2
