2021-2022学年高中数学人教版A版(2019)选择性必修一2.5.2圆与圆的位置关系 课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一2.5.2圆与圆的位置关系 课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:05:56 | ||
图片预览






文档简介
(共21张PPT)
2.5.2 圆与圆的位置关系
前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系.
我们知道,两个圆之间存在以下三种位置关系:
(1) 两圆相交,有两个公共点;
(2) 两圆相切,包括外切与内切,只有一个公共点;
(3) 两圆相离,包括外离与内含,没有公共点.
思考
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
圆和圆的位置关系
二、新课讲解
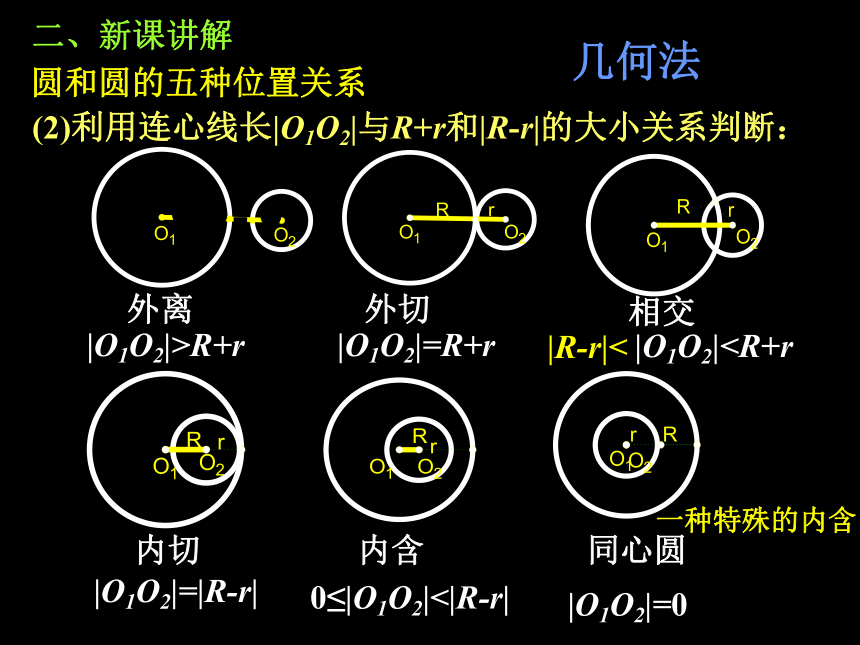
外离
外切
相交
内含
内切
圆C1:(x-a)2+(y-b)2=R2(R>0)
圆C2:(x-c)2+(y-d)2=r2(r>0)
二、新课讲解
(1) 利用两个圆的方程组成方程组的实数解的个数:
n=0
两个圆相离(外离、内含)
n=1
两个圆相切(外切、内切)
n=2
两个圆相交
代数法
圆和圆的五种位置关系
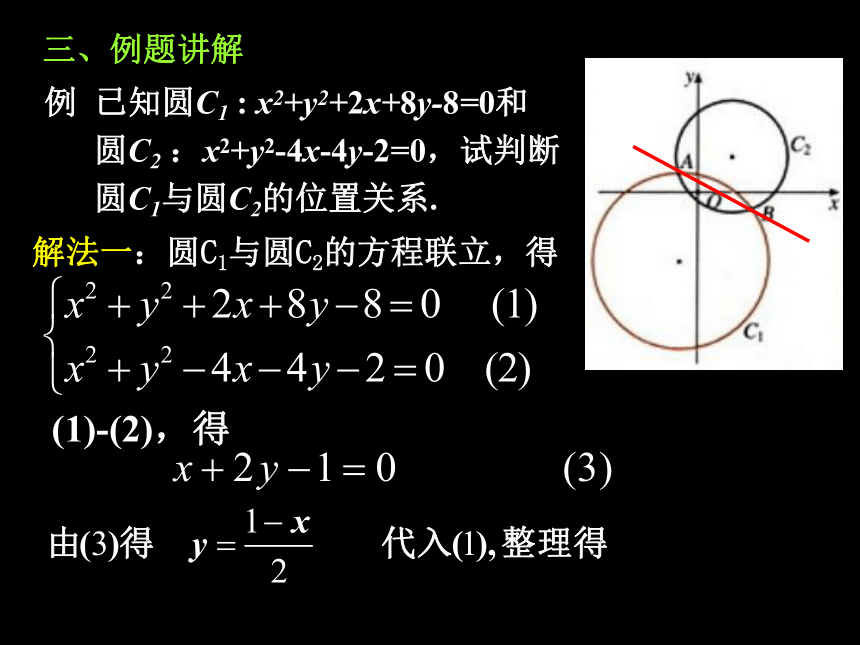
外离
|O1O2|>R+r
|O1O2|=R+r
外切
相交
|O1O2|内切
|O1O2|=|R-r|
内含
0≤|O1O2|<|R-r|
同心圆
|O1O2|=0
一种特殊的内含
二、新课讲解
(2)利用连心线长|O1O2|与R+r和|R-r|的大小关系判断:
几何法
|R-r|<
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
解法一:圆C1与圆C2的方程联立,得
(1)-(2),得
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1,y2
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
解法二:
把圆C1和圆C2的方程化为标准方程:
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
所以圆C1与圆C2相交,它们有两个公共点A,B.
补充. 已知圆C1:(x+1)2+(y-3)2=9圆C2:x2+y2-4x+2y-11=0,求两圆的公共弦所在的直线及公共弦长.
2.5.2 圆与圆的位置关系
前面我们运用直线的方程、圆的方程,研究了直线与圆的位置关系.现在我们类比上述研究方法,运用圆的方程,通过定量计算研究圆与圆的位置关系.
我们知道,两个圆之间存在以下三种位置关系:
(1) 两圆相交,有两个公共点;
(2) 两圆相切,包括外切与内切,只有一个公共点;
(3) 两圆相离,包括外离与内含,没有公共点.
思考
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的位置关系?
圆和圆的位置关系
二、新课讲解
外离
外切
相交
内含
内切
圆C1:(x-a)2+(y-b)2=R2(R>0)
圆C2:(x-c)2+(y-d)2=r2(r>0)
二、新课讲解
(1) 利用两个圆的方程组成方程组的实数解的个数:
n=0
两个圆相离(外离、内含)
n=1
两个圆相切(外切、内切)
n=2
两个圆相交
代数法
圆和圆的五种位置关系
外离
|O1O2|>R+r
|O1O2|=R+r
外切
相交
|O1O2|
|O1O2|=|R-r|
内含
0≤|O1O2|<|R-r|
同心圆
|O1O2|=0
一种特殊的内含
二、新课讲解
(2)利用连心线长|O1O2|与R+r和|R-r|的大小关系判断:
几何法
|R-r|<
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
解法一:圆C1与圆C2的方程联立,得
(1)-(2),得
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
所以,方程(4)有两个不相等的实数根x1,x2,把x1,x2分别代入方程(3),得到y1,y2
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
解法二:
把圆C1和圆C2的方程化为标准方程:
例 已知圆C1 : x2+y2+2x+8y-8=0和
圆C2 :x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.
三、例题讲解
所以圆C1与圆C2相交,它们有两个公共点A,B.
补充. 已知圆C1:(x+1)2+(y-3)2=9圆C2:x2+y2-4x+2y-11=0,求两圆的公共弦所在的直线及公共弦长.
