2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.1椭圆及其标准方程(第2课时) (共20张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.1椭圆及其标准方程(第2课时) (共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 829.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.1.1 椭圆及其标准方程
(第2课时)
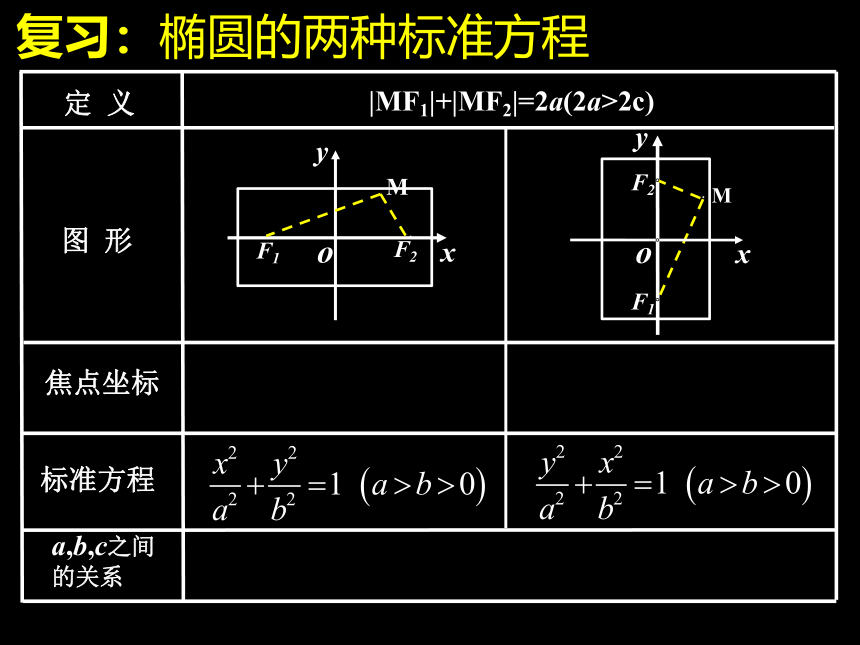
复习:椭圆的两种标准方程
y
o
F1
F2
M
x
y
x
o
F2
F1
M
定 义
图 形
标准方程
焦点坐标
a,b,c之间的关系
|MF1|+|MF2|=2a(2a>2c)
2.已知椭圆的方程为 ,则a=_____,b=_____,c=_____,焦点坐标为_______________,焦距等于_____.
1.已知椭圆的方程为 ,则a=_____,b=_____,c=_____,焦点坐标为_______________,焦距等于_____.
5
4
3
(-4,0),(4,0)
8
2
4
(0,-2),(0,2)
练习:
3
练习:
1、下列方程可以表示椭圆吗?若可以,求出焦点坐标。
圆
2.已知方程 若它表示:
(1) 椭圆,则m的取值范围: ;
(2)焦点在y轴上的椭圆,则m的取值范围: ;
(3) 焦距为4的椭圆,则m的取值范围: 。
思考:有无方法可以避开对焦点位置的讨论?
练习1.
求椭圆标准方程的步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用定义或待定系数法
确定a、b的值,
(4)写出椭圆的标准方程.
练习1.
则c=2,即a2-b2=4 ①
②
由① ②可求得a2=12,b2=8
故所求椭圆的标准方程为
(焦点在x轴)
(焦点在y轴)
故所求椭圆的标准方程为
m>0,n>0且m≠n
|m|≠|n|≠0
m>0、n>0且m≠n
m、n、l同号且m≠n
例3. 设点A、B的坐标分别为(-5,0)、(5,0),直线AM、
BM相交于点M,且它们的斜率之积是-4/9,求点M的轨
迹方程。
练习2.已知B、C是两个定点,|BC|=8,且△ABC的周长为18,求顶点A的轨迹方程.
A
B
C
x
y
O
解:以BC所在直线为x轴,线段BC的中垂线为y轴
建立直角坐标系
∵△ABC的周长为18 ,|BC|=8
∴|AB|+|AC|=10
故点A的轨迹是椭圆
∴可设点A的轨迹方程为
则2a=10,2c=8,即a=5,c=4
∴b2=25-16=9
∵A、B、C三点必须构成三角形
∴点A的轨迹方程为
x
y
P
C
M
解:∵x2+y2-6x-55=0可化为(x-3)2+y2=64
∴圆心C的坐标为(3,0),半径r=8
∵动圆M与圆C内切,且|MP|为动圆的半径
∴|MC|=8-|MP|,即|MC|+|MP|=8
∵|PC|=6<8
∴点M的轨迹是一个椭圆
∵原点恰好是PC的中点
∴可设点M的轨迹方程为
x
y
P
C
M
∴可设点M的轨迹方程为:
则2a=8,即a=4
∵c=3
∴b2=16-9=7
故动圆圆心M的轨迹方程为
… |MC|+|MP|=8 , |PC|=6<8.
x
y
O
P
M
练习4.在圆x +y =4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
D
小结:
一.求椭圆方程的基本方法:
(1)定义法:
(2)待定系数法:
二.设椭圆方程的方法:
作业:
3.1.1 椭圆及其标准方程
(第2课时)
复习:椭圆的两种标准方程
y
o
F1
F2
M
x
y
x
o
F2
F1
M
定 义
图 形
标准方程
焦点坐标
a,b,c之间的关系
|MF1|+|MF2|=2a(2a>2c)
2.已知椭圆的方程为 ,则a=_____,b=_____,c=_____,焦点坐标为_______________,焦距等于_____.
1.已知椭圆的方程为 ,则a=_____,b=_____,c=_____,焦点坐标为_______________,焦距等于_____.
5
4
3
(-4,0),(4,0)
8
2
4
(0,-2),(0,2)
练习:
3
练习:
1、下列方程可以表示椭圆吗?若可以,求出焦点坐标。
圆
2.已知方程 若它表示:
(1) 椭圆,则m的取值范围: ;
(2)焦点在y轴上的椭圆,则m的取值范围: ;
(3) 焦距为4的椭圆,则m的取值范围: 。
思考:有无方法可以避开对焦点位置的讨论?
练习1.
求椭圆标准方程的步骤:
(1)确定焦点的位置;
(2)设出椭圆的标准方程;
(3)用定义或待定系数法
确定a、b的值,
(4)写出椭圆的标准方程.
练习1.
则c=2,即a2-b2=4 ①
②
由① ②可求得a2=12,b2=8
故所求椭圆的标准方程为
(焦点在x轴)
(焦点在y轴)
故所求椭圆的标准方程为
m>0,n>0且m≠n
|m|≠|n|≠0
m>0、n>0且m≠n
m、n、l同号且m≠n
例3. 设点A、B的坐标分别为(-5,0)、(5,0),直线AM、
BM相交于点M,且它们的斜率之积是-4/9,求点M的轨
迹方程。
练习2.已知B、C是两个定点,|BC|=8,且△ABC的周长为18,求顶点A的轨迹方程.
A
B
C
x
y
O
解:以BC所在直线为x轴,线段BC的中垂线为y轴
建立直角坐标系
∵△ABC的周长为18 ,|BC|=8
∴|AB|+|AC|=10
故点A的轨迹是椭圆
∴可设点A的轨迹方程为
则2a=10,2c=8,即a=5,c=4
∴b2=25-16=9
∵A、B、C三点必须构成三角形
∴点A的轨迹方程为
x
y
P
C
M
解:∵x2+y2-6x-55=0可化为(x-3)2+y2=64
∴圆心C的坐标为(3,0),半径r=8
∵动圆M与圆C内切,且|MP|为动圆的半径
∴|MC|=8-|MP|,即|MC|+|MP|=8
∵|PC|=6<8
∴点M的轨迹是一个椭圆
∵原点恰好是PC的中点
∴可设点M的轨迹方程为
x
y
P
C
M
∴可设点M的轨迹方程为:
则2a=8,即a=4
∵c=3
∴b2=16-9=7
故动圆圆心M的轨迹方程为
… |MC|+|MP|=8 , |PC|=6<8.
x
y
O
P
M
练习4.在圆x +y =4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
D
小结:
一.求椭圆方程的基本方法:
(1)定义法:
(2)待定系数法:
二.设椭圆方程的方法:
作业:
