2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.2椭圆的简单性质(第一课时) 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.1.2椭圆的简单性质(第一课时) 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:10:43 | ||
图片预览







文档简介
(共23张PPT)
3.1.2 椭圆的简单性质
练习2.已知B、C是两个定点,|BC|=8,且△ABC的周长为18,求顶点A的轨迹方程.
A
B
C
x
y
O
解:以BC所在直线为x轴,线段BC的中垂线为y轴
建立直角坐标系
∵△ABC的周长为18 ,|BC|=8
∴|AB|+|AC|=10
故点A的轨迹是椭圆
∴可设点A的轨迹方程为
则2a=10,2c=8,即a=5,c=4
∴b2=25-16=9
∵A、B、C三点必须构成三角形
∴点A的轨迹方程为
x
y
P
C
M
解:∵x2+y2-6x-55=0可化为(x-3)2+y2=64
∴圆心C的坐标为(3,0),半径r=8
∵动圆M与圆C内切,且|MP|为动圆的半径
∴|MC|=8-|MP|,即|MC|+|MP|=8
∵|PC|=6<8
∴点M的轨迹是一个椭圆
∵原点恰好是PC的中点
∴可设点M的轨迹方程为
x
y
P
C
M
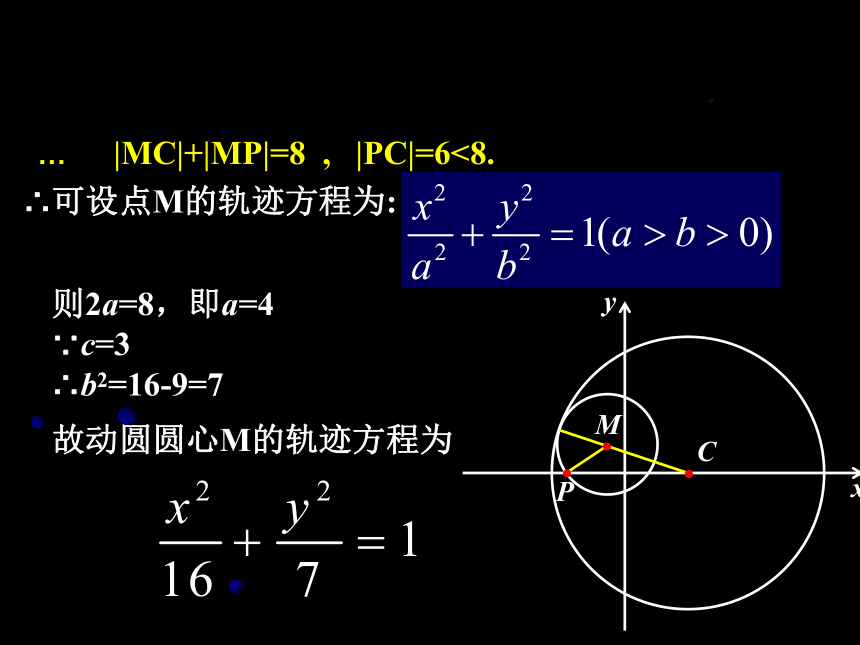
∴可设点M的轨迹方程为:
则2a=8,即a=4
∵c=3
∴b2=16-9=7
故动圆圆心M的轨迹方程为
… |MC|+|MP|=8 , |PC|=6<8.
x
y
O
P
M
练习4.在圆x +y =4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
D
小结:
一.求椭圆方程的基本方法:
(1)定义法:
(2)待定系数法:
二.设椭圆方程的方法:
复习:椭圆的定义
平面上到两个定点的距离的和等于定长2a (大于2c)
的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)
x
y
O
F1
F2
椭圆的定义的几何意义:
椭圆:
焦点: F1 ( ), F2( )
焦距:
顶点: (椭圆与坐标轴的交点)
范围 : (x、y的取值范围)
对称性:
x
y
O
F1
F2
A1
B2
A2
B1
A1(-a, 0), A2(a, 0), B1(0, -b), B2(0, b)
椭圆关于x轴、y轴都是对称的; 关于原点成中心对称.
c
c
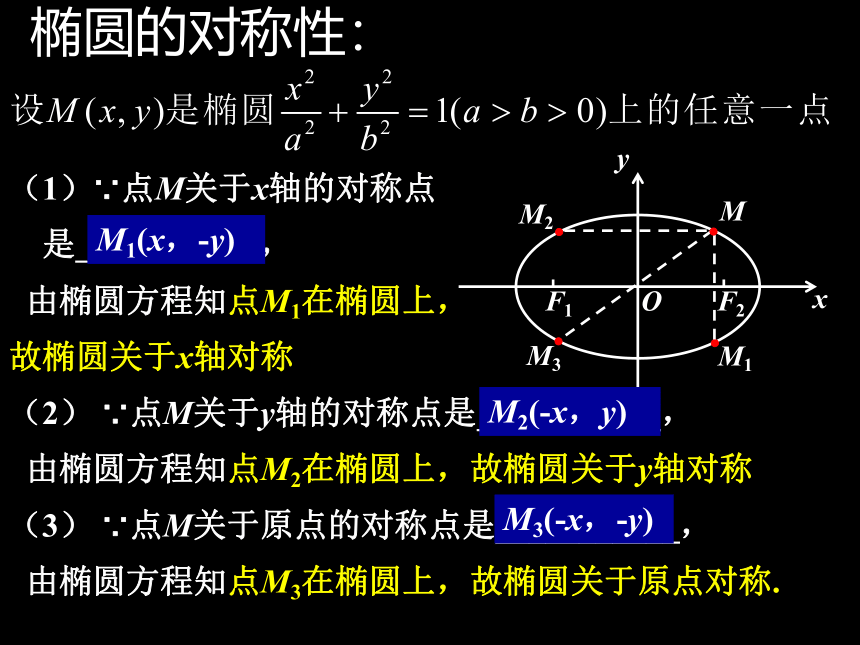
(1)∵点M关于x轴的对称点
是___________,
由椭圆方程知点M1在椭圆上,
故椭圆关于x轴对称
(2) ∵点M关于y轴的对称点是___________,
由椭圆方程知点M2在椭圆上,故椭圆关于y轴对称
(3) ∵点M关于原点的对称点是___________,
由椭圆方程知点M3在椭圆上,故椭圆关于原点对称.
椭圆的对称性:
x
y
O
F1
F2
M2
M1
M3
M1(x,-y)
M2(-x,y)
M3(-x,-y)
M
小结论:判断曲线对称性的方法
(1)在曲线方程中用-y代y,若方程不变,
则曲线关于x轴对称;
(2)在曲线方程中用-x代x,若方程不变,
则曲线关于y轴对称;
(3)在曲线方程中用-x代x 、-y代y,若方程不变,
则曲线关于原点对称;
练习1.下列方程表示的曲线中,不具备关于
( )
A、x2=4 xy B、y=x2+2
C、x2-4y=1 D、9x2+y2-4x=y
D
x轴、y轴对称或 关于原点对称的性质是
保持长半轴长a不变,改变椭圆的半焦距c,
可以发现,c越接近a,椭圆越扁平.
类似地,
保持c不变,改变a的大小,则a越接近c椭圆越扁平;
而当a,c扩大或缩小相同倍数时,椭圆的形状不变
椭圆的离心率:
我们把椭圆的焦距与长轴长的比 叫做
椭圆的离心率,记为e,即
x
y
O
F1
F2
A1
B2
A2
B1
(1) 离心率的取值范围:
因为a>c> 0,所以0(2) 离心率对椭圆形状的影响:
①e越接近1:则c越接近a,即b越小,此时椭圆越扁
②e越接近0:则c越接近0,即b越大,此时椭圆越圆
③e=0:椭圆变成圆
解:把已知方程化成标准方程
椭圆的长轴长是:
离心率:
焦点坐标是:
四个顶点坐标是:
椭圆的短轴长是:
2a=10
2b=8
例1.求椭圆 16x2 + 25y2 =400的长轴和短轴的长、离心率、
焦点和顶点坐标,并用描点法画出其图形。
例1.求椭圆 16x2 + 25y2 =400的长轴和短轴的长、离心率、
焦点和顶点坐标,并用描点法画出其图形。
把已知方程变形为:
4
在0≤ x≤5的范围内算出几个点的坐标(x,y):
x 0 1 2 3 4 5
y
3.9
3.7
3.2
2.4
0
先描点画出椭圆的一部分,
x
y
O
再利用椭圆的对称性,画
出整个椭圆。
椭圆的简单画法:
椭圆四个顶点
连线成图
矩形
2、请在图中找出长度分别为a、b、c的线段:
x
y
O
F1
F2
A1
A2
B1
B2
长度为a的有:
长度为b的有:
长度为c的有:
OA1,OA2,
B2F1, B2F2,B1F1,B1F2
OB1,OB2,
OF1,OF2,
例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于3/5 。
解:(1)依题意可知,a=3,b=2
又因为长轴在x轴上,所以椭圆的标准方程为:
例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于3/5 。
解:(2)依题意知,2a=20,e=c/a=3/5
∴a=10,c=6,故b2=100-36=64
∴当椭圆的焦点在x轴上时,椭圆的标准方程为
当椭圆的焦点在y轴上时,椭圆的标准方程为
1、中心在原点,坐标轴为对称轴的椭圆,若短轴长为6,且过点(1,4),则其标准方程是 .
2、中心在原点,焦点在坐标轴上,若长轴长为18,
且两个焦点恰好将长轴三等分,则此椭圆的方程
是 .
提示:∵2a=18,2c= (1/3)×2a=6
∴a=9,c=3,b2=81-9=72
三、课堂练习
3.若椭圆的一个焦点与长轴的两个端点的距离之比为2:3,则椭圆的离心率为( )
(A)2/3 (B)1/3 (C)√3/3 (D)1/5
4.椭圆的焦点与长轴较近端点的距离为 ,焦点与短轴两端点的连线互相垂直, 求椭圆离心率及标准方程 。
D
A
K=4或K= -5/4
7、
8、
应用举例
解:建立如图所示的直角坐标系,设所求椭圆方程为
F2
F1
B
C
A
例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2上.已知BC ⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5 cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
y
F2
F1
x
o
B
C
求B点坐标?
方程
图形
范围
对称性
顶点
离心率
y
o
F1
F2
M
x
y
x
o
F2
F1
M
关于x轴、y轴、原点对称
(±a,0),(0,±b)
(±b,0),(0,±a)
3.1.2 椭圆的简单性质
练习2.已知B、C是两个定点,|BC|=8,且△ABC的周长为18,求顶点A的轨迹方程.
A
B
C
x
y
O
解:以BC所在直线为x轴,线段BC的中垂线为y轴
建立直角坐标系
∵△ABC的周长为18 ,|BC|=8
∴|AB|+|AC|=10
故点A的轨迹是椭圆
∴可设点A的轨迹方程为
则2a=10,2c=8,即a=5,c=4
∴b2=25-16=9
∵A、B、C三点必须构成三角形
∴点A的轨迹方程为
x
y
P
C
M
解:∵x2+y2-6x-55=0可化为(x-3)2+y2=64
∴圆心C的坐标为(3,0),半径r=8
∵动圆M与圆C内切,且|MP|为动圆的半径
∴|MC|=8-|MP|,即|MC|+|MP|=8
∵|PC|=6<8
∴点M的轨迹是一个椭圆
∵原点恰好是PC的中点
∴可设点M的轨迹方程为
x
y
P
C
M
∴可设点M的轨迹方程为:
则2a=8,即a=4
∵c=3
∴b2=16-9=7
故动圆圆心M的轨迹方程为
… |MC|+|MP|=8 , |PC|=6<8.
x
y
O
P
M
练习4.在圆x +y =4上任取一点P,过点P作x轴的垂线段PD,D为垂足。当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
D
小结:
一.求椭圆方程的基本方法:
(1)定义法:
(2)待定系数法:
二.设椭圆方程的方法:
复习:椭圆的定义
平面上到两个定点的距离的和等于定长2a (大于2c)
的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2c)
x
y
O
F1
F2
椭圆的定义的几何意义:
椭圆:
焦点: F1 ( ), F2( )
焦距:
顶点: (椭圆与坐标轴的交点)
范围 : (x、y的取值范围)
对称性:
x
y
O
F1
F2
A1
B2
A2
B1
A1(-a, 0), A2(a, 0), B1(0, -b), B2(0, b)
椭圆关于x轴、y轴都是对称的; 关于原点成中心对称.
c
c
(1)∵点M关于x轴的对称点
是___________,
由椭圆方程知点M1在椭圆上,
故椭圆关于x轴对称
(2) ∵点M关于y轴的对称点是___________,
由椭圆方程知点M2在椭圆上,故椭圆关于y轴对称
(3) ∵点M关于原点的对称点是___________,
由椭圆方程知点M3在椭圆上,故椭圆关于原点对称.
椭圆的对称性:
x
y
O
F1
F2
M2
M1
M3
M1(x,-y)
M2(-x,y)
M3(-x,-y)
M
小结论:判断曲线对称性的方法
(1)在曲线方程中用-y代y,若方程不变,
则曲线关于x轴对称;
(2)在曲线方程中用-x代x,若方程不变,
则曲线关于y轴对称;
(3)在曲线方程中用-x代x 、-y代y,若方程不变,
则曲线关于原点对称;
练习1.下列方程表示的曲线中,不具备关于
( )
A、x2=4 xy B、y=x2+2
C、x2-4y=1 D、9x2+y2-4x=y
D
x轴、y轴对称或 关于原点对称的性质是
保持长半轴长a不变,改变椭圆的半焦距c,
可以发现,c越接近a,椭圆越扁平.
类似地,
保持c不变,改变a的大小,则a越接近c椭圆越扁平;
而当a,c扩大或缩小相同倍数时,椭圆的形状不变
椭圆的离心率:
我们把椭圆的焦距与长轴长的比 叫做
椭圆的离心率,记为e,即
x
y
O
F1
F2
A1
B2
A2
B1
(1) 离心率的取值范围:
因为a>c> 0,所以0
①e越接近1:则c越接近a,即b越小,此时椭圆越扁
②e越接近0:则c越接近0,即b越大,此时椭圆越圆
③e=0:椭圆变成圆
解:把已知方程化成标准方程
椭圆的长轴长是:
离心率:
焦点坐标是:
四个顶点坐标是:
椭圆的短轴长是:
2a=10
2b=8
例1.求椭圆 16x2 + 25y2 =400的长轴和短轴的长、离心率、
焦点和顶点坐标,并用描点法画出其图形。
例1.求椭圆 16x2 + 25y2 =400的长轴和短轴的长、离心率、
焦点和顶点坐标,并用描点法画出其图形。
把已知方程变形为:
4
在0≤ x≤5的范围内算出几个点的坐标(x,y):
x 0 1 2 3 4 5
y
3.9
3.7
3.2
2.4
0
先描点画出椭圆的一部分,
x
y
O
再利用椭圆的对称性,画
出整个椭圆。
椭圆的简单画法:
椭圆四个顶点
连线成图
矩形
2、请在图中找出长度分别为a、b、c的线段:
x
y
O
F1
F2
A1
A2
B1
B2
长度为a的有:
长度为b的有:
长度为c的有:
OA1,OA2,
B2F1, B2F2,B1F1,B1F2
OB1,OB2,
OF1,OF2,
例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于3/5 。
解:(1)依题意可知,a=3,b=2
又因为长轴在x轴上,所以椭圆的标准方程为:
例2.求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0)、Q(0,-2);
(2)长轴的长等于20,离心率等于3/5 。
解:(2)依题意知,2a=20,e=c/a=3/5
∴a=10,c=6,故b2=100-36=64
∴当椭圆的焦点在x轴上时,椭圆的标准方程为
当椭圆的焦点在y轴上时,椭圆的标准方程为
1、中心在原点,坐标轴为对称轴的椭圆,若短轴长为6,且过点(1,4),则其标准方程是 .
2、中心在原点,焦点在坐标轴上,若长轴长为18,
且两个焦点恰好将长轴三等分,则此椭圆的方程
是 .
提示:∵2a=18,2c= (1/3)×2a=6
∴a=9,c=3,b2=81-9=72
三、课堂练习
3.若椭圆的一个焦点与长轴的两个端点的距离之比为2:3,则椭圆的离心率为( )
(A)2/3 (B)1/3 (C)√3/3 (D)1/5
4.椭圆的焦点与长轴较近端点的距离为 ,焦点与短轴两端点的连线互相垂直, 求椭圆离心率及标准方程 。
D
A
K=4或K= -5/4
7、
8、
应用举例
解:建立如图所示的直角坐标系,设所求椭圆方程为
F2
F1
B
C
A
例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上.由椭圆一个焦点F1发出的光线,经过旋转椭圆面反射后集中到另一个焦点F2上.已知BC ⊥F1F2,|F1B|=2.8cm,|F1F2|=4.5 cm.试建立适当的坐标系,求截口BAC所在椭圆的方程(精确到0.1cm).
y
F2
F1
x
o
B
C
求B点坐标?
方程
图形
范围
对称性
顶点
离心率
y
o
F1
F2
M
x
y
x
o
F2
F1
M
关于x轴、y轴、原点对称
(±a,0),(0,±b)
(±b,0),(0,±a)
