人教七上数学1.5.2科学计数法 课件(21张ppt)
文档属性
| 名称 | 人教七上数学1.5.2科学计数法 课件(21张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 17:04:44 | ||
图片预览








文档简介
(共21张PPT)
七年级上册
1.5 有理数的乘方(第2课时)
1.5.2 科学记数法
天上的星星知多少?
2003年国际天文学联合会大会上,天文学家指出,整个可见宇宙空间大约有700万亿亿颗恒星,那这个数字是多少呢?它比地球上所有沙漠和海滩上的砂砾总和还要多,也就是在“7”后面加22个“0”,
即约为70 000 000 000 000 000 000 000 颗
歼20(黑鹰)是我国研制的一款第五代双发重型隐形战斗机,它的最大飞行高度为18 000米。
情境引入
光的传播速度为每秒300 000 000米
目前宇宙的年龄为13 820 000 000年
有没有一种表示方法,能让这些大数易读易写呢
18 000
960 000
1 170 000
300 000 000
13 820 000 000
... ...
仔细观察下列各数
10
2
=____,
10
3
=_____,
10
4
=______,
观察下列数据:
那么100 000 可以表示成__________,
10 000 000 可以表示成___________,
1后面有11个零呢 ________________.
思考:
那迪士尼的游客人数 960 000 能否利用10的乘方来表示吗
100
1000
10000
10
5
10
7
10
11
探究新知
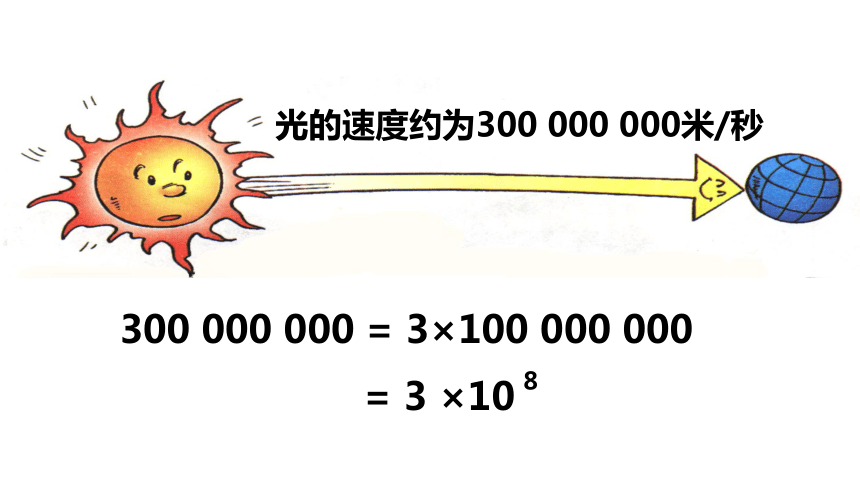
光的速度约为300 000 000米/秒
300 000 000
= 3×100 000 000
= 3 ×10
8
把一个大于10的数表示成a×10n的形式(其中1≤a<10,n是正整数),这种记数方法叫做科学记数法.
归纳新知
下列各数是否是用科学记数法表示的?
不是
不是
3 200 000
6 900 000
6 900 000
是
3 200 000
不是
3 200 000
是
理解概念
3 200 000
= 3.2×1 000 000
= 3.2×10
6
820 000
= 8.2×100 000
= 8.2×10
5
神六飞船在太空中大约飞行 3 200 000
千米
我国南沙群岛占地面积约为820 000平方
公里
在用科学记数法表示一个数的时候,怎样快速地确定出形式中的a和n呢
3 200 000
= 3.2×10
6
820 000
= 8.2×10
5
a×10n
观察
下面的式子中, 等号左边的整数位数和右边10的指数之间存在什么关系
3 200 000
= 3.2×10
6
820 000
= 8.2×10
5
a×10n中10的指数n=整数的位数-1.
总结:
5
8
m-1
a×10n 中10的指数n=整数的位数-1.
学以致用
(1)如果一个数是6位整数,用科学记数法表示它时,10的指数是_________;如果一个数有9位整数,那10的指数呢 ____________.
(2) 用科学记数法表示一个m位整数,那10的指数应是________.
例 用科学记数法表示下列各数:
1 000 000, 57 000 000, -123 000 000 000.
解:
1000 000
= 10
6
57 000 000
= 5.7×10
7
-123 000 000 000
= -1.23×10
11
对于小于-10的数也可以类似表示.
= -5.67 ×108.
例如 -567 000 000
例题讲解
1. 请用科学记数法表示下列数字:
(1)中国国家图书馆藏书大约有(200 000 000)
册;
(2)我国森林面积为(128 630 000)______________公顷;
(3)我国人口已达(1 370 000 000)____________ 人 ;
2×10
8
1.2863×10
8
1.37×10
9
(4)光年是指光一年所走过的路程,一光年约等于
(9 460 000 000 000)__________ 千米;
9.46×10
12
(5) -3 600 000=_______________;
-3.6×10
6
巩固练习:
练习2 下列用科学记数法写出的数,你知道原数分别是什么数吗
(2)2016年正月初五单日全国铁路发送旅客8.91×10 人次; 原数是___位数,为 _____________人次.
6
(1)一套《辞海》大约有1.7×10 个字;
原数是__位数,为______________个.
7
17 000 000
8 910 000
(3) -9.2×10 是___ 位数,为___________.
5
-920000
用科学记数法 a×10 表示的数写成原数时,整数位数应该是n+1
8
7
6
n
2.用科学记数法表示大数时有什么好处?
1.遇到较大的数时可用科学记数法表示.
一般形式:a×10n (1≤a<10,n为正整数)
这节课你学到些什么?
3.用科学记数法a×10n表示大数关键注意两点:
(1) 1≤a<10.
(2)n=原数整数位数-1.
课堂小结
有关资料表明,一个在刷牙过程中如果一直打开水龙头,将浪费大约7杯水(每杯水约250mL),我们某市人口除婴幼儿外,约有100万人口,如果所有的人在刷牙过程中都不关水龙头,则一次刷牙将浪费多少mL水 (用科学记数法表示)
解:
浪费的水为
250×7 ×1 000 000=1 750 000 000
= 1. 75 ×10
9
(mL)
答:一次刷牙将浪费1. 75 ×109 mL水。
应用提升
作业:
A:45页练习1,2,3
B:48页练习9,10
谢谢指导!
七年级上册
1.5 有理数的乘方(第2课时)
1.5.2 科学记数法
天上的星星知多少?
2003年国际天文学联合会大会上,天文学家指出,整个可见宇宙空间大约有700万亿亿颗恒星,那这个数字是多少呢?它比地球上所有沙漠和海滩上的砂砾总和还要多,也就是在“7”后面加22个“0”,
即约为70 000 000 000 000 000 000 000 颗
歼20(黑鹰)是我国研制的一款第五代双发重型隐形战斗机,它的最大飞行高度为18 000米。
情境引入
光的传播速度为每秒300 000 000米
目前宇宙的年龄为13 820 000 000年
有没有一种表示方法,能让这些大数易读易写呢
18 000
960 000
1 170 000
300 000 000
13 820 000 000
... ...
仔细观察下列各数
10
2
=____,
10
3
=_____,
10
4
=______,
观察下列数据:
那么100 000 可以表示成__________,
10 000 000 可以表示成___________,
1后面有11个零呢 ________________.
思考:
那迪士尼的游客人数 960 000 能否利用10的乘方来表示吗
100
1000
10000
10
5
10
7
10
11
探究新知
光的速度约为300 000 000米/秒
300 000 000
= 3×100 000 000
= 3 ×10
8
把一个大于10的数表示成a×10n的形式(其中1≤a<10,n是正整数),这种记数方法叫做科学记数法.
归纳新知
下列各数是否是用科学记数法表示的?
不是
不是
3 200 000
6 900 000
6 900 000
是
3 200 000
不是
3 200 000
是
理解概念
3 200 000
= 3.2×1 000 000
= 3.2×10
6
820 000
= 8.2×100 000
= 8.2×10
5
神六飞船在太空中大约飞行 3 200 000
千米
我国南沙群岛占地面积约为820 000平方
公里
在用科学记数法表示一个数的时候,怎样快速地确定出形式中的a和n呢
3 200 000
= 3.2×10
6
820 000
= 8.2×10
5
a×10n
观察
下面的式子中, 等号左边的整数位数和右边10的指数之间存在什么关系
3 200 000
= 3.2×10
6
820 000
= 8.2×10
5
a×10n中10的指数n=整数的位数-1.
总结:
5
8
m-1
a×10n 中10的指数n=整数的位数-1.
学以致用
(1)如果一个数是6位整数,用科学记数法表示它时,10的指数是_________;如果一个数有9位整数,那10的指数呢 ____________.
(2) 用科学记数法表示一个m位整数,那10的指数应是________.
例 用科学记数法表示下列各数:
1 000 000, 57 000 000, -123 000 000 000.
解:
1000 000
= 10
6
57 000 000
= 5.7×10
7
-123 000 000 000
= -1.23×10
11
对于小于-10的数也可以类似表示.
= -5.67 ×108.
例如 -567 000 000
例题讲解
1. 请用科学记数法表示下列数字:
(1)中国国家图书馆藏书大约有(200 000 000)
册;
(2)我国森林面积为(128 630 000)______________公顷;
(3)我国人口已达(1 370 000 000)____________ 人 ;
2×10
8
1.2863×10
8
1.37×10
9
(4)光年是指光一年所走过的路程,一光年约等于
(9 460 000 000 000)__________ 千米;
9.46×10
12
(5) -3 600 000=_______________;
-3.6×10
6
巩固练习:
练习2 下列用科学记数法写出的数,你知道原数分别是什么数吗
(2)2016年正月初五单日全国铁路发送旅客8.91×10 人次; 原数是___位数,为 _____________人次.
6
(1)一套《辞海》大约有1.7×10 个字;
原数是__位数,为______________个.
7
17 000 000
8 910 000
(3) -9.2×10 是___ 位数,为___________.
5
-920000
用科学记数法 a×10 表示的数写成原数时,整数位数应该是n+1
8
7
6
n
2.用科学记数法表示大数时有什么好处?
1.遇到较大的数时可用科学记数法表示.
一般形式:a×10n (1≤a<10,n为正整数)
这节课你学到些什么?
3.用科学记数法a×10n表示大数关键注意两点:
(1) 1≤a<10.
(2)n=原数整数位数-1.
课堂小结
有关资料表明,一个在刷牙过程中如果一直打开水龙头,将浪费大约7杯水(每杯水约250mL),我们某市人口除婴幼儿外,约有100万人口,如果所有的人在刷牙过程中都不关水龙头,则一次刷牙将浪费多少mL水 (用科学记数法表示)
解:
浪费的水为
250×7 ×1 000 000=1 750 000 000
= 1. 75 ×10
9
(mL)
答:一次刷牙将浪费1. 75 ×109 mL水。
应用提升
作业:
A:45页练习1,2,3
B:48页练习9,10
谢谢指导!
