九年级第23章旋转导学案
图片预览


文档简介
课题 23.1图形的旋转1 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1.旋转的相关概念2.旋转的变换的特点重点:理解并掌握旋转的相关概念难点:观察与空间想象
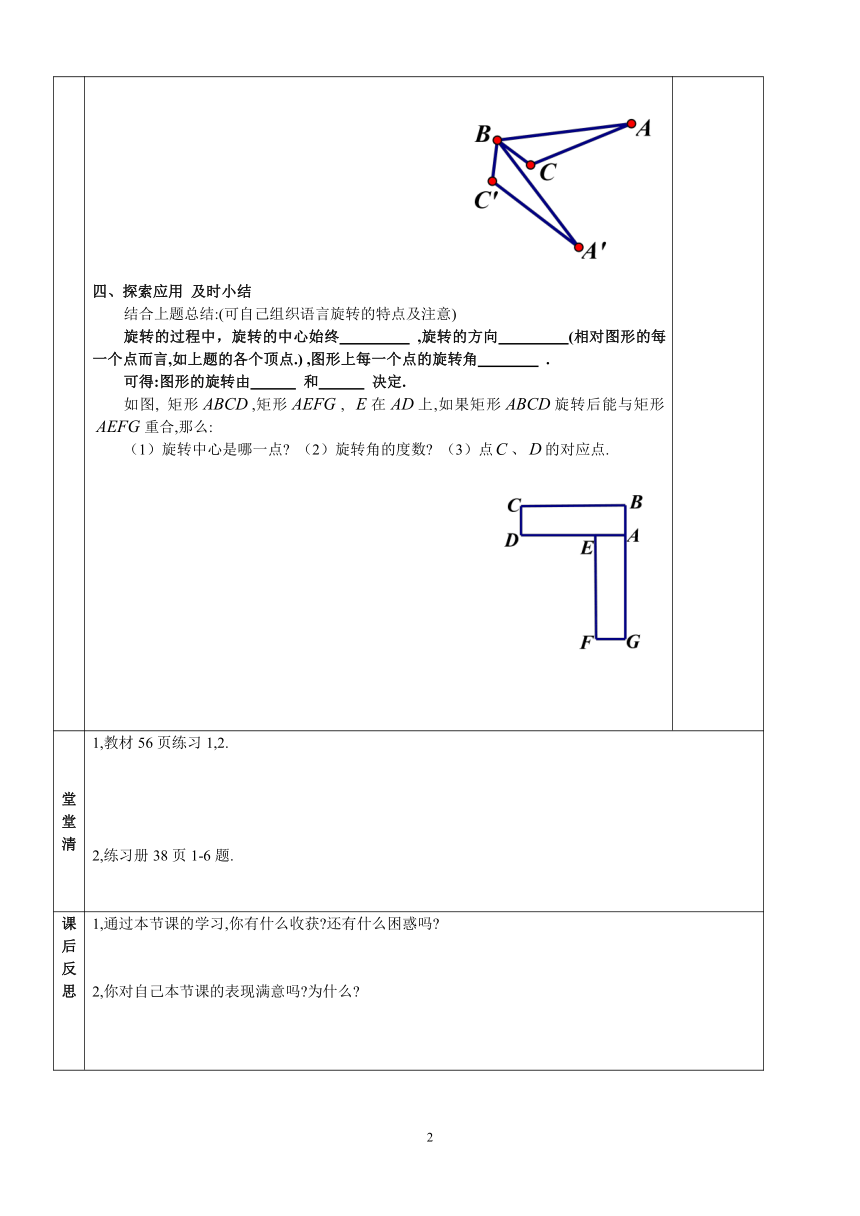
教学程序 一、创设情境 引入新课前面我们学习了图形变换—平移,它的特点与性质 你荡过秋千、玩过陀螺、见过飞机的螺旋桨吧 游乐园的大转盘,学习了地球的自转、公转等;这些物体都是转动的,它们把我们带进了一个旋转的世界. 二、交流探究 学习新知探究1:仔细观察下面图片,钟表的指针在不停的转动,从11时到12时时针转动了多少度 风车的每个叶片在风的作用转到不同的位置. 它们有什么特点 这些特点相同么 旋转的概念:总结旋转的概念(自己组织语言,交流总结) 上面的指针、叶片等可以看作是一个平面图形,把一个图形绕着某一点转到了一个角度的图形变换叫做 ,点叫做 ,转动的角叫做 .如果图形上的点经过旋转变为,那么这两个点叫做这个旋转的 . 讨论:你在生活中还见过那些旋转的物体 三、应用新知 反馈演练 已知把绕着点顺时针旋转后能与重合. 求:(1)找出旋转中心; (2)指出对应定点和对应边; (3)指出旋转角. 四、探索应用 及时小结结合上题总结:(可自己组织语言旋转的特点及注意)旋转的过程中,旋转的中心始终 ,旋转的方向 (相对图形的每一个点而言,如上题的各个顶点.) ,图形上每一个点的旋转角 .可得:图形的旋转由 和 决定.如图, 矩形,矩形, 在上,如果矩形旋转后能与矩形重合,那么:(1)旋转中心是哪一点 (2)旋转角的度数 (3)点、的对应点.
堂堂清 1,教材56页练习1,2.2,练习册38页1-6题.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.1图形的旋转2 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1旋转的基本特征,旋转图形的画法重点:旋转的特征难点:旋转的中心
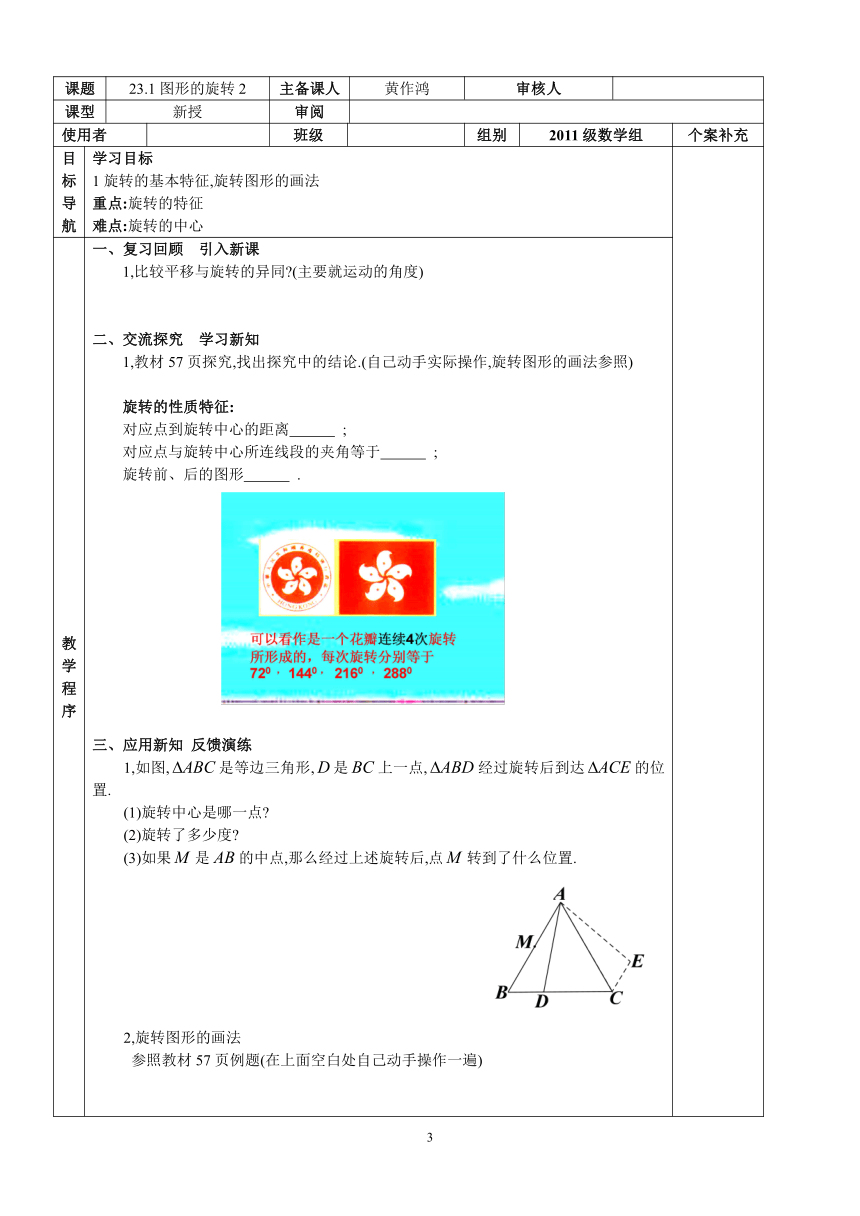
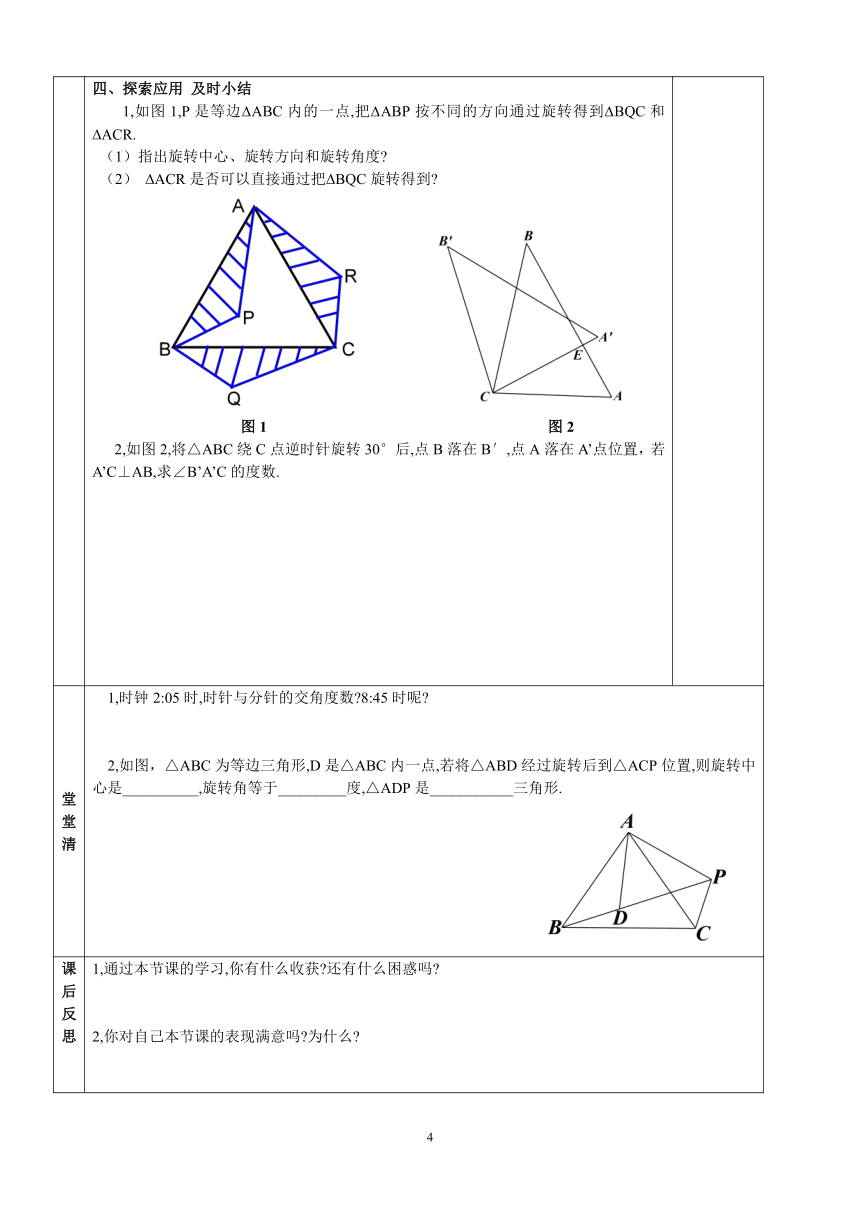
教学程序 一、复习回顾 引入新课1,比较平移与旋转的异同 (主要就运动的角度)二、交流探究 学习新知1,教材57页探究,找出探究中的结论.(自己动手实际操作,旋转图形的画法参照)旋转的性质特征:对应点到旋转中心的距离 ;对应点与旋转中心所连线段的夹角等于 ;旋转前、后的图形 .三、应用新知 反馈演练1,如图,是等边三角形,是上一点,经过旋转后到达的位置.(1)旋转中心是哪一点 (2)旋转了多少度 (3)如果是的中点,那么经过上述旋转后,点转到了什么位置.2,旋转图形的画法 参照教材57页例题(在上面空白处自己动手操作一遍)四、探索应用 及时小结 1,如图1,P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR. (1)指出旋转中心、旋转方向和旋转角度 (2) ACR是否可以直接通过把BQC旋转得到 图1 图2 2,如图2,将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,求∠B’A’C的度数.
堂堂清 1,时钟2:05时,时针与分针的交角度数 8:45时呢 2,如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.1中心对称 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1中心对称的概念2中心对称的性质3作一个图形关于某点成中心对称的对称图形重点:中心对称的性质难点:中心对称作法
教学程序 一、复习回顾 引入新课 把一个图形绕着某一个点旋转,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点成 ,这个点叫做 ,这两个图形中的对应点叫做关于中心的 .(结合上面观察)指出上面图2的对称中心 各顶点关于中心的对称点 二、交流探究 学习新知探究:认真阅读教材63页探究内容,利用手中的三角板自己动手操作并得出结论. 把结论试证明如下:(可组内交流)新知:中心对称两个图形,对称点连线段都经过 ,且被对称中心 .中心对称的两个图形是 .中心对称的尺规作图:(自己参照动手实验)三、应用新知 反馈演练已知四边形和点,求作四边形,使四边形和四边形关于点成中心对称.(要写出必要的解题过程)提示:关键是作出点、、、关于点的对称点、、、. 四、探索应用 及时小结中心对称和轴对称的区别和联系:中心对称是关于 对称;轴对称是关于 对称.中心对称是由 而得;轴对称是由 而得.两者都是涉及 个图形,都是 个图形之间的关系.(各具体关系 )如图,已知和关于点成中心对称,求作对称中心点.
堂堂清 教材64页练习1,2.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.2中心对称图形 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1中心对称图形的概念2识别中心对称图形(线段,平行四边形)重点:中心对称图形的识别难点:中心对称图形的对称中心
教学程序 一、复习回顾 引入新课1,中心对称的概念及性质 2,观察并结论3,探究:教材65页”思考”,得出结论.二、交流探究 学习新知 中心对称图形的定义根据上(一)可归纳:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做 ,这个点就是它的 .如:上面思考中的线段和平行四边形都是对称中心图形,请找出它们的对称中心 三、应用新知 反馈演练1,判断下列图形是否为中心对称图形,如果是,请指出它们的对称中心.线段; 平行四边形; 矩形; 菱形; 正方形; 园; 角,等腰三角形. 指示:判断一个图形是否为中心对称图形,关键是找到一个点,看绕着该点旋转后能否与自身重合.(请与中心对称加以区别和联系,教师引导)四、探索应用 及时小结观察并结论.
堂堂清 1,教材66页练习1,2. 2,那些是中心对称图形 3,按要求画一个图形,所画图形中同时要有一个正方形和一个圆,并且这个圆形即是轴对称图形又是中心对称图形(自己动手画画,交流看谁画的又准确又多 )
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.3关于原点对称的点的坐标 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标在平面直角坐标系下两个点关于原点对称时的坐标规律重点: 关于原点对称时的坐标规律难点: 关于原点对称时的坐标规律的应用
教学程序 一、复习回顾 引入新课1,八年级我们学习了在平面直角坐标系下点关于轴和轴对称的坐标规律,请你写出其规律,并在坐标系下描出几个点,再描出其关于轴和轴对称的坐标. 2,能在坐标系下作出关于原点对称的点的坐标么 二、交流探究 学习新知在同一平面直角坐标系下描出,,,,,并作它们关于原点对称的点、、、,.(自己建立坐标作答)由上面的例子可得下面规律:两个点关于原点对称,它们的坐标符号相反,即点关于原点的对称点为.教材67页例2三、应用新知 反馈演练1,下列各点哪些点关于原点对称 那些关于坐标轴对称 ,,,,,,2,下列函数中,图象一定关于原点对称的图象是( ) A,; B,; C,; D,以上三种都不可能.四、探索应用 及时小结1,写出函数与的共同性质.(从对称的角度写)*2,如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线.(1)在图中画出直线;(2)求出线段中点的反比例函数解析式;(3)是否存在另一条与直线AB平行的直线,它与双曲线只有一个交点,若存在,求此直线的函数解析式,若不存在,请说明理由.
堂堂清 1,教材67页练习.2,如果点与点关于原点对称,求,的值.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23章.旋转.习题课 主备课人 黄作鸿 审核人
课型 习题课 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标主要是加强前面所有课时的重点、难点突破
教学程序 1,教材59页1题2,教材60页4题(自己动手画图作答)3,教材60页5题(自己动手画图作答)4,教材61页8题5,教材61页10题6,教材67页1题(请就教材上作答)7,教材68页2题(教材上作答),3,4题8,教材68页5,7题(自己动手画图作答)
堂堂清 1,练习册38页2,3题2,练习册38页4题(下面空白处作答)3,练习册38—39页5—7题4,练习册39页8题(下面空白处作答)5,练习册40页1---6题6,练习册41页9题(下面空白处作答)7,练习册43页1—3题,43—44页5---8题8,练习册44页10题(下面空白处作答)
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
PAGE
3
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1.旋转的相关概念2.旋转的变换的特点重点:理解并掌握旋转的相关概念难点:观察与空间想象
教学程序 一、创设情境 引入新课前面我们学习了图形变换—平移,它的特点与性质 你荡过秋千、玩过陀螺、见过飞机的螺旋桨吧 游乐园的大转盘,学习了地球的自转、公转等;这些物体都是转动的,它们把我们带进了一个旋转的世界. 二、交流探究 学习新知探究1:仔细观察下面图片,钟表的指针在不停的转动,从11时到12时时针转动了多少度 风车的每个叶片在风的作用转到不同的位置. 它们有什么特点 这些特点相同么 旋转的概念:总结旋转的概念(自己组织语言,交流总结) 上面的指针、叶片等可以看作是一个平面图形,把一个图形绕着某一点转到了一个角度的图形变换叫做 ,点叫做 ,转动的角叫做 .如果图形上的点经过旋转变为,那么这两个点叫做这个旋转的 . 讨论:你在生活中还见过那些旋转的物体 三、应用新知 反馈演练 已知把绕着点顺时针旋转后能与重合. 求:(1)找出旋转中心; (2)指出对应定点和对应边; (3)指出旋转角. 四、探索应用 及时小结结合上题总结:(可自己组织语言旋转的特点及注意)旋转的过程中,旋转的中心始终 ,旋转的方向 (相对图形的每一个点而言,如上题的各个顶点.) ,图形上每一个点的旋转角 .可得:图形的旋转由 和 决定.如图, 矩形,矩形, 在上,如果矩形旋转后能与矩形重合,那么:(1)旋转中心是哪一点 (2)旋转角的度数 (3)点、的对应点.
堂堂清 1,教材56页练习1,2.2,练习册38页1-6题.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.1图形的旋转2 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1旋转的基本特征,旋转图形的画法重点:旋转的特征难点:旋转的中心
教学程序 一、复习回顾 引入新课1,比较平移与旋转的异同 (主要就运动的角度)二、交流探究 学习新知1,教材57页探究,找出探究中的结论.(自己动手实际操作,旋转图形的画法参照)旋转的性质特征:对应点到旋转中心的距离 ;对应点与旋转中心所连线段的夹角等于 ;旋转前、后的图形 .三、应用新知 反馈演练1,如图,是等边三角形,是上一点,经过旋转后到达的位置.(1)旋转中心是哪一点 (2)旋转了多少度 (3)如果是的中点,那么经过上述旋转后,点转到了什么位置.2,旋转图形的画法 参照教材57页例题(在上面空白处自己动手操作一遍)四、探索应用 及时小结 1,如图1,P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR. (1)指出旋转中心、旋转方向和旋转角度 (2) ACR是否可以直接通过把BQC旋转得到 图1 图2 2,如图2,将△ABC绕C点逆时针旋转30°后,点B落在B′,点A落在A’点位置,若A’C⊥AB,求∠B’A’C的度数.
堂堂清 1,时钟2:05时,时针与分针的交角度数 8:45时呢 2,如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.1中心对称 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1中心对称的概念2中心对称的性质3作一个图形关于某点成中心对称的对称图形重点:中心对称的性质难点:中心对称作法
教学程序 一、复习回顾 引入新课 把一个图形绕着某一个点旋转,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点成 ,这个点叫做 ,这两个图形中的对应点叫做关于中心的 .(结合上面观察)指出上面图2的对称中心 各顶点关于中心的对称点 二、交流探究 学习新知探究:认真阅读教材63页探究内容,利用手中的三角板自己动手操作并得出结论. 把结论试证明如下:(可组内交流)新知:中心对称两个图形,对称点连线段都经过 ,且被对称中心 .中心对称的两个图形是 .中心对称的尺规作图:(自己参照动手实验)三、应用新知 反馈演练已知四边形和点,求作四边形,使四边形和四边形关于点成中心对称.(要写出必要的解题过程)提示:关键是作出点、、、关于点的对称点、、、. 四、探索应用 及时小结中心对称和轴对称的区别和联系:中心对称是关于 对称;轴对称是关于 对称.中心对称是由 而得;轴对称是由 而得.两者都是涉及 个图形,都是 个图形之间的关系.(各具体关系 )如图,已知和关于点成中心对称,求作对称中心点.
堂堂清 教材64页练习1,2.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.2中心对称图形 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标1中心对称图形的概念2识别中心对称图形(线段,平行四边形)重点:中心对称图形的识别难点:中心对称图形的对称中心
教学程序 一、复习回顾 引入新课1,中心对称的概念及性质 2,观察并结论3,探究:教材65页”思考”,得出结论.二、交流探究 学习新知 中心对称图形的定义根据上(一)可归纳:把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做 ,这个点就是它的 .如:上面思考中的线段和平行四边形都是对称中心图形,请找出它们的对称中心 三、应用新知 反馈演练1,判断下列图形是否为中心对称图形,如果是,请指出它们的对称中心.线段; 平行四边形; 矩形; 菱形; 正方形; 园; 角,等腰三角形. 指示:判断一个图形是否为中心对称图形,关键是找到一个点,看绕着该点旋转后能否与自身重合.(请与中心对称加以区别和联系,教师引导)四、探索应用 及时小结观察并结论.
堂堂清 1,教材66页练习1,2. 2,那些是中心对称图形 3,按要求画一个图形,所画图形中同时要有一个正方形和一个圆,并且这个圆形即是轴对称图形又是中心对称图形(自己动手画画,交流看谁画的又准确又多 )
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23.2.3关于原点对称的点的坐标 主备课人 黄作鸿 审核人
课型 新授 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标在平面直角坐标系下两个点关于原点对称时的坐标规律重点: 关于原点对称时的坐标规律难点: 关于原点对称时的坐标规律的应用
教学程序 一、复习回顾 引入新课1,八年级我们学习了在平面直角坐标系下点关于轴和轴对称的坐标规律,请你写出其规律,并在坐标系下描出几个点,再描出其关于轴和轴对称的坐标. 2,能在坐标系下作出关于原点对称的点的坐标么 二、交流探究 学习新知在同一平面直角坐标系下描出,,,,,并作它们关于原点对称的点、、、,.(自己建立坐标作答)由上面的例子可得下面规律:两个点关于原点对称,它们的坐标符号相反,即点关于原点的对称点为.教材67页例2三、应用新知 反馈演练1,下列各点哪些点关于原点对称 那些关于坐标轴对称 ,,,,,,2,下列函数中,图象一定关于原点对称的图象是( ) A,; B,; C,; D,以上三种都不可能.四、探索应用 及时小结1,写出函数与的共同性质.(从对称的角度写)*2,如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线.(1)在图中画出直线;(2)求出线段中点的反比例函数解析式;(3)是否存在另一条与直线AB平行的直线,它与双曲线只有一个交点,若存在,求此直线的函数解析式,若不存在,请说明理由.
堂堂清 1,教材67页练习.2,如果点与点关于原点对称,求,的值.
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
课题 23章.旋转.习题课 主备课人 黄作鸿 审核人
课型 习题课 审阅
使用者 班级 组别 2011级数学组 个案补充
目标导航 学习目标主要是加强前面所有课时的重点、难点突破
教学程序 1,教材59页1题2,教材60页4题(自己动手画图作答)3,教材60页5题(自己动手画图作答)4,教材61页8题5,教材61页10题6,教材67页1题(请就教材上作答)7,教材68页2题(教材上作答),3,4题8,教材68页5,7题(自己动手画图作答)
堂堂清 1,练习册38页2,3题2,练习册38页4题(下面空白处作答)3,练习册38—39页5—7题4,练习册39页8题(下面空白处作答)5,练习册40页1---6题6,练习册41页9题(下面空白处作答)7,练习册43页1—3题,43—44页5---8题8,练习册44页10题(下面空白处作答)
课后反思 1,通过本节课的学习,你有什么收获 还有什么困惑吗 2,你对自己本节课的表现满意吗 为什么
PAGE
3
同课章节目录
