安徽六安市汇文中学2021-2022学年九年级上期末联考模拟数学试卷(WORD版,含答案)
文档属性
| 名称 | 安徽六安市汇文中学2021-2022学年九年级上期末联考模拟数学试卷(WORD版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览


文档简介
安徽六安市汇文中学2021-2022学年九上期末联考模拟数学试卷
温馨提示:本试卷内容涵盖沪科版21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 二次函数y=–3x2+2图象的顶点坐标为( )
A. (0,0) B. ( -3,–2) C. ( –3,2) D. (0,2)
2.己知点A(1,–3)关于x轴的对称点A'在反比例函数y=的图像上,则实数k的值为( )
A. 3 B. C. -3 D. -
3.在 Rt△ACB中,∠C = 90°,AC = 1,BC = 2,则sin B的值为( )
A. B. C. D.
4.如图所示,AB是⊙O的直径,C、D为⊙O上的两点,若∠CAB=35°,则∠D等于( )
A. 35° B. 55° C. 65 D. 70°
第4题图 第5题图 第6题图 第9题图
5.如图,在平行四边形ABCD中,F是BC边上一点,延长DF交AB的延长线于点E,若AB=3BE,则BF:CF等于( )
A. 1:2 B. 1:3 C. 2:3 D. 2:5
6.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A. 1.8 B. 3.2 C. 2.4 D. 5
7.已知二次函数y= –x2+2x,当–1A. a>1 B. –1<a≤1 C. a>0 D. –1<a<2
8.点A(m,n)在二次函数y=x2–4的图象上,则2m–n的最大值是( )
A.4 B. 5 C. –4 D. –5
9.如图,在△ABC中,∠ACB = 90°,D点在BC边上,=,P为AB边上一点,当PC = PD时,的值为( )
A. B. C. D.
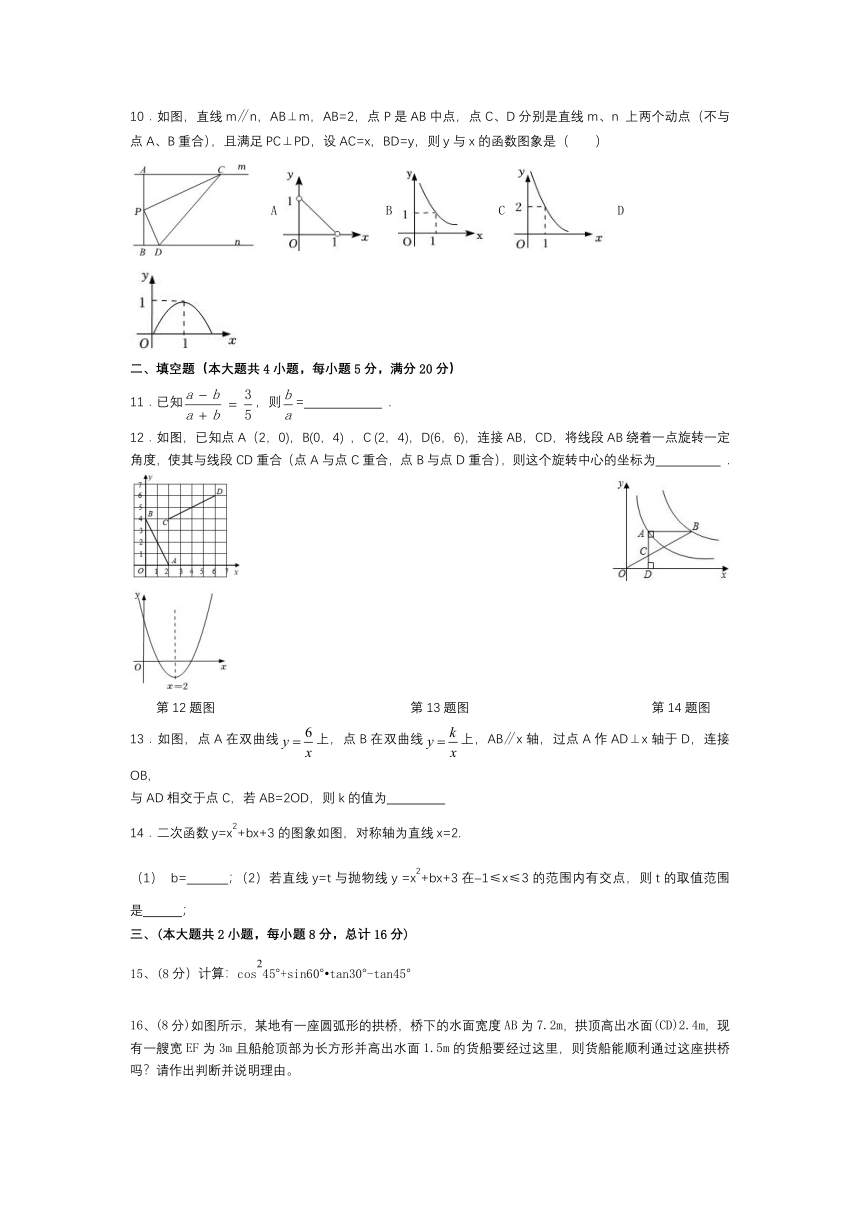
10.如图,直线m∥n,AB⊥m,AB=2,点P是AB中点,点C、D分别是直线m、n 上两个动点(不与点A、B重合),且满足PC⊥PD,设AC=x,BD=y,则y与x的函数图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则= .
12.如图,已知点A(2,0),B(0,4) ,C (2,4),D(6,6),连接AB,CD,将线段AB绕着一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
第12题图 第13题图 第14题图
13.如图,点A在双曲线上,点B在双曲线上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,
与AD相交于点C,若AB=2OD,则k的值为
14.二次函数y=x2+bx+3的图象如图,对称轴为直线x=2.
(1) b= ;(2)若直线y=t与抛物线y =x2+bx+3在–1≤x≤3的范围内有交点,则t的取值范围是 ;
三、(本大题共2小题,每小题8分,总计16分)
15、(8分)计算:cos45°+sin60° tan30°-tan45°
16、(8分)如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由。
四、(本大题共2小题,每小题8分,总计16分)
17、(8分)马路边上有一棵树AB,树底A距离护路坡CD的底端D有3米,斜坡CD的坡角为60度,小明发现,下午2点时太阳光下该树的影子恰好为AD,同时刻1米长的竹竿影长为0.5米,下午4点时又发现该树的部分影子落在斜坡CD上的DE处,且BE⊥CD,如图所示.
(1)树AB的高度是 米; (2)求DE的长.
18、(8分)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A (0,3)、B (3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)﹒
(1)画出△ABC以点О为中心,顺时针方向旋转90°,得到的A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
五、(本大题共2小题,每小题10分,总计20分)
19、(10分)如图,圆O中两条互相垂直的弦AB、CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长; (2)点F在CD上,且CE=EF,求证AF⊥BD.
20、(10分)在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
六、(本大题共1小题,每小题12分,总计12分)
21、(12分)如图,一次函数y=-x+tb与反比例函数(x>0)的图象交于点A(m,4)和B(4,1)
(1)求b、k、m的值;
(2)根据图象直接写出-x+b<(x>0)的解集;
(3)点Р是线段AB上一点,过点Р作PD⊥x轴于点D,连接OP,若ΔPOD 的面积为S,求S的最大值和最小值;
七、(本大题共1小题,每小题12分,总计12分)
22、(12分)规定:不相交的两个函数图象在竖直方向上的最短距离为这两个函数的“亲近距离”
(1)求抛物线y =x-2x+3与x轴的“亲近距离”;
(2)在探究问题:求抛物线y=x-2x+3与直线y=x-1的“亲近距离”的过程中,有人提出:过抛物线的顶点向x轴作垂线与直线相交,则该问题的“亲近距离”一定是抛物线顶点与交点之间的距离,你同意他的看法吗?请说明理由;
(3)若抛物线y=x-2x+3与抛物线y=x+c的“亲近距离”为,求c的值.
八、(本大题共1小题,每小题14分,总计14分)
23、(14分)如图1,在△ABC 中,∠ACB=90°,AC=BC,E为△ABC的中线BD上的一点,将线段AE以E点为中心逆时针旋转90度得到线段FE,FE恰好经过点C。
(1)若∠CAF=α,则∠CBE= (用含α的代数式表示);
(2)若BH平分∠EBC,交EC于点G,交AF于点H,如图2。
①求证:△BEG ~△ACF; ②若EG=1,求CF的长。
安徽六安市汇文中学2021-2022学年九上期末联考模拟数学试卷答案
1 2 3 4 5 6 7 8 9 10
D A B B B B B B A B
11、 12、 (4,2); 13、 18; 14、 (1)b=-4; (2) -1≤t≤8; 15、0;
17、(1)6; (2)(3-)米;
18、(1)C1(2,-2)如图所示; (2)C2(1,0),如图所示:; (3)2.5;
20、
(2)4.5;
21、
22、(1)2;
(3)c=1
温馨提示:本试卷内容涵盖沪科版21.1~24.3、共4页八大题、23小题,满分150分,时间120分钟
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 二次函数y=–3x2+2图象的顶点坐标为( )
A. (0,0) B. ( -3,–2) C. ( –3,2) D. (0,2)
2.己知点A(1,–3)关于x轴的对称点A'在反比例函数y=的图像上,则实数k的值为( )
A. 3 B. C. -3 D. -
3.在 Rt△ACB中,∠C = 90°,AC = 1,BC = 2,则sin B的值为( )
A. B. C. D.
4.如图所示,AB是⊙O的直径,C、D为⊙O上的两点,若∠CAB=35°,则∠D等于( )
A. 35° B. 55° C. 65 D. 70°
第4题图 第5题图 第6题图 第9题图
5.如图,在平行四边形ABCD中,F是BC边上一点,延长DF交AB的延长线于点E,若AB=3BE,则BF:CF等于( )
A. 1:2 B. 1:3 C. 2:3 D. 2:5
6.如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若AB=4,AC=3,则BD为( )
A. 1.8 B. 3.2 C. 2.4 D. 5
7.已知二次函数y= –x2+2x,当–1
8.点A(m,n)在二次函数y=x2–4的图象上,则2m–n的最大值是( )
A.4 B. 5 C. –4 D. –5
9.如图,在△ABC中,∠ACB = 90°,D点在BC边上,=,P为AB边上一点,当PC = PD时,的值为( )
A. B. C. D.
10.如图,直线m∥n,AB⊥m,AB=2,点P是AB中点,点C、D分别是直线m、n 上两个动点(不与点A、B重合),且满足PC⊥PD,设AC=x,BD=y,则y与x的函数图象是( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则= .
12.如图,已知点A(2,0),B(0,4) ,C (2,4),D(6,6),连接AB,CD,将线段AB绕着一点旋转一定角度,使其与线段CD重合(点A与点C重合,点B与点D重合),则这个旋转中心的坐标为 .
第12题图 第13题图 第14题图
13.如图,点A在双曲线上,点B在双曲线上,AB∥x轴,过点A作AD⊥x轴于D,连接OB,
与AD相交于点C,若AB=2OD,则k的值为
14.二次函数y=x2+bx+3的图象如图,对称轴为直线x=2.
(1) b= ;(2)若直线y=t与抛物线y =x2+bx+3在–1≤x≤3的范围内有交点,则t的取值范围是 ;
三、(本大题共2小题,每小题8分,总计16分)
15、(8分)计算:cos45°+sin60° tan30°-tan45°
16、(8分)如图所示,某地有一座圆弧形的拱桥,桥下的水面宽度AB为7.2m,拱顶高出水面(CD)2.4m,现有一艘宽EF为3m且船舱顶部为长方形并高出水面1.5m的货船要经过这里,则货船能顺利通过这座拱桥吗?请作出判断并说明理由。
四、(本大题共2小题,每小题8分,总计16分)
17、(8分)马路边上有一棵树AB,树底A距离护路坡CD的底端D有3米,斜坡CD的坡角为60度,小明发现,下午2点时太阳光下该树的影子恰好为AD,同时刻1米长的竹竿影长为0.5米,下午4点时又发现该树的部分影子落在斜坡CD上的DE处,且BE⊥CD,如图所示.
(1)树AB的高度是 米; (2)求DE的长.
18、(8分)已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A (0,3)、B (3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度)﹒
(1)画出△ABC以点О为中心,顺时针方向旋转90°,得到的A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
五、(本大题共2小题,每小题10分,总计20分)
19、(10分)如图,圆O中两条互相垂直的弦AB、CD交于点E.
(1)M是CD的中点,OM=3,CD=12,求圆O的半径长; (2)点F在CD上,且CE=EF,求证AF⊥BD.
20、(10分)在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD;
(2)若DE=3,BC=8,求△FCD的面积.
六、(本大题共1小题,每小题12分,总计12分)
21、(12分)如图,一次函数y=-x+tb与反比例函数(x>0)的图象交于点A(m,4)和B(4,1)
(1)求b、k、m的值;
(2)根据图象直接写出-x+b<(x>0)的解集;
(3)点Р是线段AB上一点,过点Р作PD⊥x轴于点D,连接OP,若ΔPOD 的面积为S,求S的最大值和最小值;
七、(本大题共1小题,每小题12分,总计12分)
22、(12分)规定:不相交的两个函数图象在竖直方向上的最短距离为这两个函数的“亲近距离”
(1)求抛物线y =x-2x+3与x轴的“亲近距离”;
(2)在探究问题:求抛物线y=x-2x+3与直线y=x-1的“亲近距离”的过程中,有人提出:过抛物线的顶点向x轴作垂线与直线相交,则该问题的“亲近距离”一定是抛物线顶点与交点之间的距离,你同意他的看法吗?请说明理由;
(3)若抛物线y=x-2x+3与抛物线y=x+c的“亲近距离”为,求c的值.
八、(本大题共1小题,每小题14分,总计14分)
23、(14分)如图1,在△ABC 中,∠ACB=90°,AC=BC,E为△ABC的中线BD上的一点,将线段AE以E点为中心逆时针旋转90度得到线段FE,FE恰好经过点C。
(1)若∠CAF=α,则∠CBE= (用含α的代数式表示);
(2)若BH平分∠EBC,交EC于点G,交AF于点H,如图2。
①求证:△BEG ~△ACF; ②若EG=1,求CF的长。
安徽六安市汇文中学2021-2022学年九上期末联考模拟数学试卷答案
1 2 3 4 5 6 7 8 9 10
D A B B B B B B A B
11、 12、 (4,2); 13、 18; 14、 (1)b=-4; (2) -1≤t≤8; 15、0;
17、(1)6; (2)(3-)米;
18、(1)C1(2,-2)如图所示; (2)C2(1,0),如图所示:; (3)2.5;
20、
(2)4.5;
21、
22、(1)2;
(3)c=1
同课章节目录
