安徽省芜湖市市区2021-2022学年九年级上学期12月月考数学试题(PDF版含答案)
文档属性
| 名称 | 安徽省芜湖市市区2021-2022学年九年级上学期12月月考数学试题(PDF版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 15:08:16 | ||
图片预览


文档简介
2021—2022学年度第一学期月考试卷(十二月月考)
九年级数学
(答题时间 120 分钟,满分 150 分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
得分 评卷人 一、选择题:每小题给出的四个选项中,其中只有一个是正确的
器.请
把正确选项的代号写在下面的答题表内(本大题共 10 小题,每
题 4分,共 40 分)
答 题 栏
题号 1 2 3 4 5 6 7 辑8 9 10
答案
1.下列垃圾分类标识中,是中心对称图形的是( )编.
A. B. FC. D.
2.一元二次方程 2x2+x=P3的二次项D系数、一次项系数、常数项分别是( ).A.2,0,3 B.2,1,3 C.2,0,-3 D.2,1,-33.在下列抛物线中,其顶点是(-2,4)的是( ).
A. y=(x+2)2﹣4 B.y=(x-2)2+4 C.y=(x+2)2+4 D. y=(x-2)2﹣4
4.如图所云示,将△ABC绕点 A逆时针旋转至△ADE,则旋转角为( ).A.∠BAD B.∠BAC C.∠BAE D.∠CAD
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点 为圆心,AC为半径作⊙A,那么斜
风边 AB的中点 D与⊙A的位置关系是( ).A.点 D在⊙A外 B.点 D在⊙A上 C.点 D在⊙A内 D.无法确定
6.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
九年级数学十二月月考试卷 第 1 页 (共 8 页)
九年级数学
学校 班级 姓名 准考证号
… … … … … 装 … … … … 订 … … … … 线 … … … … 内 … … … … 不 … … … … 得 … … … … 答 … … … … … 题 … … … … … …
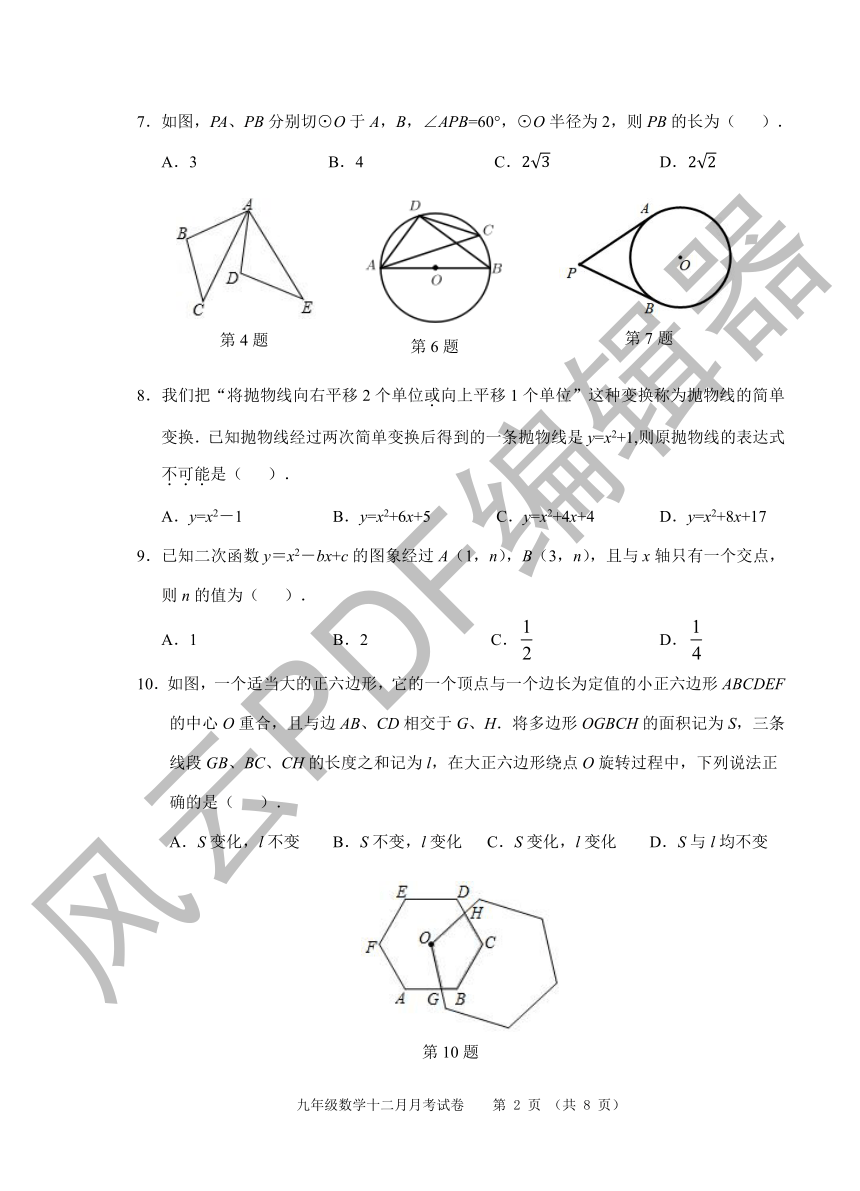
7.如图,PA、PB分别切⊙O于 A,B,∠APB=60°,⊙O半径为 2,则 PB的长为( ).
A.3 B.4 C.2 3 D.2 2
第 4题 第 7题第 6题 器
8.我们把“将抛物线向右平移 2个单位或.向上平移 1个单位”这种变辑换称为抛物线的简单变换.已知抛物线经过两次简单变换后得到的一条抛物线是 y=x2+1,则原抛物线的表达式不.可.能.是( ).
A.y=x2-1 B.y=x2+6x+5 C.y=x2+4x+4 D.y=x2+8x+17
9.已知二次函数 y=x2-bx+c的图象经过 A(F1,n),编B(3,n),且与 x轴只有一个交点,则 n的值为( ). 1 1A.1 B.2 C. D.
2 4
10.如图,一个适当大的P正六边形,它的一个顶点与一个边长为定值的小正六边形 ABCDEF的中心 O重合,且与边 AB、CD相交于 G、H.将多边形 OGBCH的面积记为 S,三条线段 GB、BC、CH的长度之和记为 l,在大正六边形绕点 O旋转过程中,下列说法正
确的是( ).
A.S云变化,l不变 B.S不变,l变化 C.S变化,l变化 D.S与 l均不变
风
第 10题
九年级数学十二月月考试卷 第 2 页 (共 8 页)
得分 评卷人
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
11.将抛物线 y=x2+1沿 x轴向下翻折,则得到的新抛物线的解析式为 .
12.如图,在⊙O中, � = 2 � ,AD⊥OC于点 D,比较大小 AB 2AD.
(填入“>”或“<”或“=”).
13.如图,在矩形 ABCD中,AB=4,BC=6,E是矩形 ABCD内部的一个动点,且 AE⊥BE,
则线段 CE的最小值为 . 器
辑
第 12题 编第 13题
14.设二次函数 y=x2+2x-3的图象为 C1,关F于 x的一次函数 y=kx+3k的图象为 C2.
(1)C1和 C2恰好都经过定点 P,则点 P的坐标为 ;
(2)若 C1和 C2有两个不P同的交点D,设其横坐标分别为 x1和 x2,且 x1<x2<1,则 k的取值范围为 .
得分 评卷人 三、(本大题 2 个小题,每小题 8 分,共 16 分)
15.解方云程: x2 3x 2 0.
风
九年级数学十二月月考试卷 第 3 页 (共 8 页)
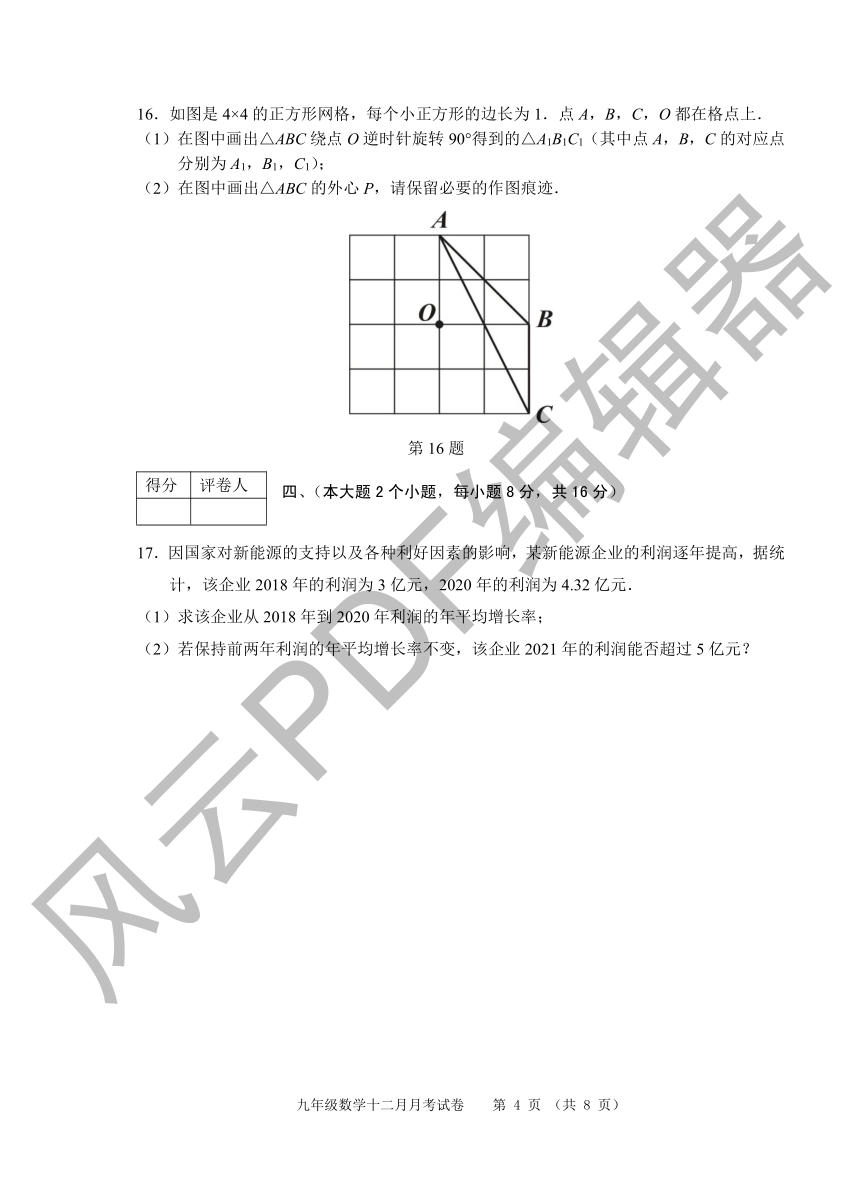
16.如图是 4×4的正方形网格,每个小正方形的边长为 1.点 A,B,C,O都在格点上.
(1)在图中画出△ABC绕点 O逆时针旋转 90°得到的△A1B1C1(其中点 A,B,C的对应点
分别为 A1,B1,C1);
(2)在图中画出△ABC的外心 P,请保留必要的作图痕迹.
器
第 16题 辑
得分 评卷人 四、(本大题 2 个小题,每小题 8 分,共 16 分)
17.因国家对新能源的支持以及各种利好因素F的影响,编某新能源企业的利润逐年提高,据统计,该企业 2018年的利润为 3亿元,2020年的利润为 4.32亿元.(1)求该企业从 2018年到 2020年利润的年平均增长率;
(2)若保持前两年利润的年平均增D长率不变,该企业 2021年的利润能否超过 5亿元?P
云
风
九年级数学十二月月考试卷 第 4 页 (共 8 页)
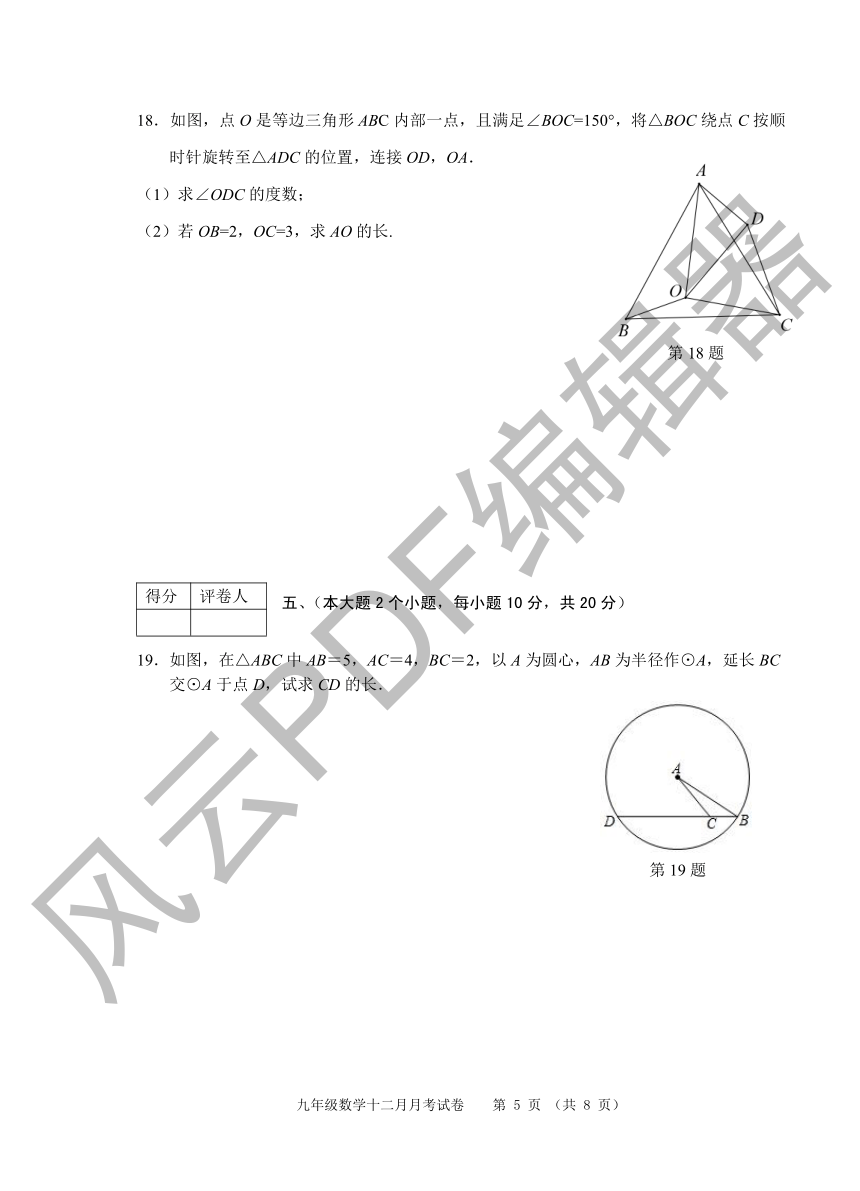
18.如图,点 O是等边三角形 ABC内部一点,且满足∠BOC=150°,将△BOC绕点 C按顺
时针旋转至△ADC的位置,连接 OD,OA.
(1)求∠ODC的度数;
(2)若 OB=2,OC=3,求 AO的长.
第 18题器
辑
编
得分 评卷人 五、(本大题 2 个小题,每F小题 10 分,共 20 分)
19.如图,在△ABC中 AB=5,ACD=4,BC=2,以 A为圆心,AB为半径作⊙A,延长 BC交⊙A于点 D,试求PCD的长.
云 第 19题
风
九年级数学十二月月考试卷 第 5 页 (共 8 页)
20.已知二次函数 y=-x2+4x-3.
(1)若-3≤x≤3,则 y的取值范围为 (直接写出结果);
(2)若-8≤y≤-3,则 x的取值范围为 (直接写出结果);
3
(3)若 A(m,y1),B(m+1,y2)两点都在该函数的图象上,且满足 m< ,试比较 y1与 y2的
2
大小,并说明理由.
器
得分 评卷人 六、(本题满分 12 分) 辑
21.如图,△ABC中,∠ACB=90°,点 O在边 AC上,经过点 C的⊙O与斜边 AB相切于
点 D,交 AC边于点 E.
1
(1)求证:∠ACD= ∠B;
2 编
(2)若 BC=6,AC=8,求 AD和 CD的长.F
PD 第 21题
云
风
九年级数学十二月月考试卷 第 6 页 (共 8 页)
得分 评卷人 七、(本题满分 12 分)
22.某饰品店以 20元/件的价格采购了一批今年新上市的饰品进行了为期 30天的销售,销
售结束后,分析得知日销售量 P(件)与销售时间 x(天)之间有如下关系:P=-
2x+80(1≤x≤30);又知前 20天的销售价格 Q1(元/件)与销售时间 x(天)之间有如下关
1
系:Q1= x+30(1≤x≤20),后 10天的销售价格 Q2则稳定在 45元/件.
2
(1)试分别写出该商店前 20天的日销售利润 R1(元)和后 10天的日销售利润 R2(元器)与销售间 x(天)之间的函数关系式;
(2)请问在这 30 天的销售期中,哪一天的日销售利润最大?请求出这个最大利润值是多
少?(注:销售利润=销售收入-购进成本) 辑
F编
PD
云
风
九年级数学十二月月考试卷 第 7 页 (共 8 页)
得分 评卷人 八、(本题满分 14 分) …
…
23.如图,抛物线 y=-x2+bx+c与 x轴交于 A,B两点,其中 A(3,0),B(-1,0),
…
与 y轴交于点 C,抛物线的对称轴交 x轴于点 D,直线 y=kx+b1经过点 A、C,连接 CD.
(1)分别求抛物线和直线 AC的解析式; …
(2)在直线 AC下方的抛物线上,是否存在一点 P,使得△ACP的面积是△ACD面积的 2 答
倍,若存在,请求出点 P的坐标;若不存在,请说明理由; …
(3)在抛物线的对称轴上是否存在一点 Q,使线段 AQ绕.Q.点.顺.时.针.旋转 90°得到线段器QA1, …且点 A1恰好落在该抛物线上?若存在,求出点 Q的坐标;若不存在,请说明理由. ……
题
辑 ………
…
编 不……
第 23题 F 备用图 …D …过…P ………此…
云 ………
线
风 ………
…
…
九年级数学十二月月考试卷 第 8 页 (共 8 页)
2021—2022学年度第一学期月考试卷(十二月月考)
数学参考答案及评分标准
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1.B 2.D 3.C 4.A 5.A 6.C 7.C 8.B 9.A 10.D
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
11. y=-x2-1;12. =;13.2 10 2;14.(1)(-3,0)(2分)(2)k<0且 k≠-4(器3分)
三、(本大题 2 个小题,每小题 8 分,共 16 分)
15.解:(x-1)(x-2)=0 (4分) 辑
x 1 0或 x 2 0 .
x1 1, x2 2. (8分)
16.解:(1)如图所示 (4分) 编
(2)利用网格分别作 BC,AB 的垂直平分线交于点 P,
则点 P 为△ABC 外接圆的圆心. (8 分) F
四、(本大题 2 个小题,每小题 8 分D,共 16 分)17.解:(1)设该企业P从 2018年到 2020年利润的年平均增长率为 x.(1 分)根据题意得 3(1+x)2=4.32. (4 分)
解得 x1 =0.2=20%,x2 =-2.2(不合题意,舍去).
答:该企云业从 2018年到 2020年利润的年平均增长率为 20%.(6 分)(2)如果仍保持相同的年平均增长率,
那么该企业的 2021 年的利润为 4.32(1+20%)=5.184>5.
风答:该企业 2017 年的利润能超过 5 亿元 . (8 分)18.解:(1)由旋转的性质得,CD=CO,∠ACD=∠BCO.(1分)
∵∠ACB=60°,∴∠DCO=60°,
∴△OCD为等边三角形. (3分)
九年级数学十二月月考试卷 第 9 页 (共 8 页)
∴∠ODC=60°. (4分)
(2)由旋转的性质得,AD=OB=2. (5分)
∵△OCD为等边三角形,∴OD=OC=3 (6分)
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°. (7分)
在 Rt△AOD中, AO= 13 . (8分)
五、(本大题 2 个小题,每小题 10 分,共 20 分) 器
19.解:如图,过点 A作 AE⊥BD于点 E,连接 AD.(2分)
∴AD=AB=5,
根据垂径定理,得 DE=BE, 辑
∴CE=BE﹣BC=DE﹣2. (4分)
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2, 编
∴52﹣DE2=42﹣(DE﹣2)2,
13 F
解得 DE= . (8分)
4
∴CD=DE+CE=2DE﹣2P= 9. (10分)2 D20.解:(1)-24≤y≤1 (2分)(2)-1≤x≤0或 4≤x≤5 (6分)
(3)由题云意,y1=-m
2+4m-3,y2=-(m+1)2+4(m+1)-3
则 y1-y2=2m-3 (8分)
3
又 m< ,∴2m-3<0,即 y1<y2. (10分)
2
风六、(本题满分 12 分)21.(1)证明:如图,连接 OD. (1分)
∵AB为切线,∴OD⊥AB,∴∠ODB=90°.
∵∠ACB=90°,∴∠ABC+∠COD=180°.
九年级数学十二月月考试卷 第 10 页 (共 8 页)
∵∠AOD+∠COD=180°,∴∠AOD=∠ABC.(4分)
∵∠AOD=2∠ACD,∴∠ACD= 1∠ABC. (6分)
2
(2)解:在 Rt△ABC中,AB= 62 + 82 =10,
∵OC⊥CB,∴BC为切线,∴BD=BC=6,∴AD=4. (8分)
设⊙O的半径为 r,则 OD=OC=r,OA=8﹣r,
在 Rt△AOD中,r2+42=(8﹣r)2,解得 r=3,∴OC=3. (9分)
如图,连接 OB交 CD于 H. 器
∵OC=OD,BC=BD,∴OB垂直平分 CD. (10分)
在 Rt△OCB中,OB= 32 + 62 =3 5,
1
∵ OB CH= 1OC BC CH= 3×6,∴ = 6 5, 辑
2 2 3 5 5
12 5
∴CD=2CH= . (12分)
5
七、(本题满分 12 分) 编
1
22.解:(1)根据题意,得 R1=P(Q1-20)=(-2x+ 80F)[( x+30)-20]= -x2+20x+800(3分)2
R2=P(Q2-20)=(-2x+80)(45-20)= -50xD+2000 (5分)(2)当 1≤x≤20时,R1=-(x-10)2+900,
当 x=10时,R1的最大值为 900; (8分)
当 21≤x≤30时,R2=-50Px+2000.
R2的值随 x值的增大而减小,
当 x=21时云,R2的最大值是 950. (10分)∵950>900,
风∴在第 21天时,日销售利润最大,最大利润为 950元. (12分)八、(本题满分 14 分)
23.(1)把 A(3,0),B(-1,0)代入 y=-x2+bx+c,
解得 b=2,c=3.∴抛物线的解析式为 y=-x2+2x+3.(2分)
九年级数学十二月月考试卷 第 11 页 (共 8 页)
则 C点为(0,3).又 A(3,0),代入 y=kx+b1,
得 k=-1,b1=3. ∴直线 AC的解析式为 y=-x+3. (4分)
(2)当 P点与 B点重合时,连接 PC,此时 DP=DA.
则△ACP 的面积是△ACD面积的 2倍,即 P为(-1,0). (5分)
过 B点作 BP∥AC交抛物线于点 P,即为所求,
此时直线 BP的解析式为 y=-x-1. (6分)
与抛物线解析式 y=-x2+2x+3联立, 器
解得 x=-1,y=0;或者 x=4,y=-5.所以(4,-5)为所求.
综上,点 P的坐标为(-1,0)或(4,-5) (8分)
(3)由(1)可知,抛物线解析式为 y=-(x-1)2+4 辑
把 x=1代入直线 AC解析式 y=-x+3,
得 AC与抛物线对称轴的交点M(1,2),如右图所示.
则△MAB是等腰直角三角形,符合题意. 编
M点即为所求 Q点的一种情况. (10分)
当 Q点在 x轴下方时,设 Q为(1,m),mF<0.
因为线段 AQ绕 Q点顺时针旋转 90°得到线段 QA1,
过 A1作直线 DQ的垂线于PE点,则D△ADQ≌△QEA1. (11分)∴AD=QE=2,DQ=EA1=-m.∴A1(1-m,m-2). (12分)
∵点 A1恰云好落在抛物线 y=-x2+2x+3上,代入,解得 m=-3(舍去 m=2).∴Q(1,-3)综上,Q点坐标为(1,2)或(1,-3). (14分)
风【说明:以上解法不唯一,只要合理,均应给分】
九年级数学十二月月考试卷 第 12 页 (共 8 页)
九年级数学
(答题时间 120 分钟,满分 150 分)
题 号 一 二 三 四 五 六 七 八 总 分
得 分
得分 评卷人 一、选择题:每小题给出的四个选项中,其中只有一个是正确的
器.请
把正确选项的代号写在下面的答题表内(本大题共 10 小题,每
题 4分,共 40 分)
答 题 栏
题号 1 2 3 4 5 6 7 辑8 9 10
答案
1.下列垃圾分类标识中,是中心对称图形的是( )编.
A. B. FC. D.
2.一元二次方程 2x2+x=P3的二次项D系数、一次项系数、常数项分别是( ).A.2,0,3 B.2,1,3 C.2,0,-3 D.2,1,-33.在下列抛物线中,其顶点是(-2,4)的是( ).
A. y=(x+2)2﹣4 B.y=(x-2)2+4 C.y=(x+2)2+4 D. y=(x-2)2﹣4
4.如图所云示,将△ABC绕点 A逆时针旋转至△ADE,则旋转角为( ).A.∠BAD B.∠BAC C.∠BAE D.∠CAD
5.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点 为圆心,AC为半径作⊙A,那么斜
风边 AB的中点 D与⊙A的位置关系是( ).A.点 D在⊙A外 B.点 D在⊙A上 C.点 D在⊙A内 D.无法确定
6.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
九年级数学十二月月考试卷 第 1 页 (共 8 页)
九年级数学
学校 班级 姓名 准考证号
… … … … … 装 … … … … 订 … … … … 线 … … … … 内 … … … … 不 … … … … 得 … … … … 答 … … … … … 题 … … … … … …
7.如图,PA、PB分别切⊙O于 A,B,∠APB=60°,⊙O半径为 2,则 PB的长为( ).
A.3 B.4 C.2 3 D.2 2
第 4题 第 7题第 6题 器
8.我们把“将抛物线向右平移 2个单位或.向上平移 1个单位”这种变辑换称为抛物线的简单变换.已知抛物线经过两次简单变换后得到的一条抛物线是 y=x2+1,则原抛物线的表达式不.可.能.是( ).
A.y=x2-1 B.y=x2+6x+5 C.y=x2+4x+4 D.y=x2+8x+17
9.已知二次函数 y=x2-bx+c的图象经过 A(F1,n),编B(3,n),且与 x轴只有一个交点,则 n的值为( ). 1 1A.1 B.2 C. D.
2 4
10.如图,一个适当大的P正六边形,它的一个顶点与一个边长为定值的小正六边形 ABCDEF的中心 O重合,且与边 AB、CD相交于 G、H.将多边形 OGBCH的面积记为 S,三条线段 GB、BC、CH的长度之和记为 l,在大正六边形绕点 O旋转过程中,下列说法正
确的是( ).
A.S云变化,l不变 B.S不变,l变化 C.S变化,l变化 D.S与 l均不变
风
第 10题
九年级数学十二月月考试卷 第 2 页 (共 8 页)
得分 评卷人
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
11.将抛物线 y=x2+1沿 x轴向下翻折,则得到的新抛物线的解析式为 .
12.如图,在⊙O中, � = 2 � ,AD⊥OC于点 D,比较大小 AB 2AD.
(填入“>”或“<”或“=”).
13.如图,在矩形 ABCD中,AB=4,BC=6,E是矩形 ABCD内部的一个动点,且 AE⊥BE,
则线段 CE的最小值为 . 器
辑
第 12题 编第 13题
14.设二次函数 y=x2+2x-3的图象为 C1,关F于 x的一次函数 y=kx+3k的图象为 C2.
(1)C1和 C2恰好都经过定点 P,则点 P的坐标为 ;
(2)若 C1和 C2有两个不P同的交点D,设其横坐标分别为 x1和 x2,且 x1<x2<1,则 k的取值范围为 .
得分 评卷人 三、(本大题 2 个小题,每小题 8 分,共 16 分)
15.解方云程: x2 3x 2 0.
风
九年级数学十二月月考试卷 第 3 页 (共 8 页)
16.如图是 4×4的正方形网格,每个小正方形的边长为 1.点 A,B,C,O都在格点上.
(1)在图中画出△ABC绕点 O逆时针旋转 90°得到的△A1B1C1(其中点 A,B,C的对应点
分别为 A1,B1,C1);
(2)在图中画出△ABC的外心 P,请保留必要的作图痕迹.
器
第 16题 辑
得分 评卷人 四、(本大题 2 个小题,每小题 8 分,共 16 分)
17.因国家对新能源的支持以及各种利好因素F的影响,编某新能源企业的利润逐年提高,据统计,该企业 2018年的利润为 3亿元,2020年的利润为 4.32亿元.(1)求该企业从 2018年到 2020年利润的年平均增长率;
(2)若保持前两年利润的年平均增D长率不变,该企业 2021年的利润能否超过 5亿元?P
云
风
九年级数学十二月月考试卷 第 4 页 (共 8 页)
18.如图,点 O是等边三角形 ABC内部一点,且满足∠BOC=150°,将△BOC绕点 C按顺
时针旋转至△ADC的位置,连接 OD,OA.
(1)求∠ODC的度数;
(2)若 OB=2,OC=3,求 AO的长.
第 18题器
辑
编
得分 评卷人 五、(本大题 2 个小题,每F小题 10 分,共 20 分)
19.如图,在△ABC中 AB=5,ACD=4,BC=2,以 A为圆心,AB为半径作⊙A,延长 BC交⊙A于点 D,试求PCD的长.
云 第 19题
风
九年级数学十二月月考试卷 第 5 页 (共 8 页)
20.已知二次函数 y=-x2+4x-3.
(1)若-3≤x≤3,则 y的取值范围为 (直接写出结果);
(2)若-8≤y≤-3,则 x的取值范围为 (直接写出结果);
3
(3)若 A(m,y1),B(m+1,y2)两点都在该函数的图象上,且满足 m< ,试比较 y1与 y2的
2
大小,并说明理由.
器
得分 评卷人 六、(本题满分 12 分) 辑
21.如图,△ABC中,∠ACB=90°,点 O在边 AC上,经过点 C的⊙O与斜边 AB相切于
点 D,交 AC边于点 E.
1
(1)求证:∠ACD= ∠B;
2 编
(2)若 BC=6,AC=8,求 AD和 CD的长.F
PD 第 21题
云
风
九年级数学十二月月考试卷 第 6 页 (共 8 页)
得分 评卷人 七、(本题满分 12 分)
22.某饰品店以 20元/件的价格采购了一批今年新上市的饰品进行了为期 30天的销售,销
售结束后,分析得知日销售量 P(件)与销售时间 x(天)之间有如下关系:P=-
2x+80(1≤x≤30);又知前 20天的销售价格 Q1(元/件)与销售时间 x(天)之间有如下关
1
系:Q1= x+30(1≤x≤20),后 10天的销售价格 Q2则稳定在 45元/件.
2
(1)试分别写出该商店前 20天的日销售利润 R1(元)和后 10天的日销售利润 R2(元器)与销售间 x(天)之间的函数关系式;
(2)请问在这 30 天的销售期中,哪一天的日销售利润最大?请求出这个最大利润值是多
少?(注:销售利润=销售收入-购进成本) 辑
F编
PD
云
风
九年级数学十二月月考试卷 第 7 页 (共 8 页)
得分 评卷人 八、(本题满分 14 分) …
…
23.如图,抛物线 y=-x2+bx+c与 x轴交于 A,B两点,其中 A(3,0),B(-1,0),
…
与 y轴交于点 C,抛物线的对称轴交 x轴于点 D,直线 y=kx+b1经过点 A、C,连接 CD.
(1)分别求抛物线和直线 AC的解析式; …
(2)在直线 AC下方的抛物线上,是否存在一点 P,使得△ACP的面积是△ACD面积的 2 答
倍,若存在,请求出点 P的坐标;若不存在,请说明理由; …
(3)在抛物线的对称轴上是否存在一点 Q,使线段 AQ绕.Q.点.顺.时.针.旋转 90°得到线段器QA1, …且点 A1恰好落在该抛物线上?若存在,求出点 Q的坐标;若不存在,请说明理由. ……
题
辑 ………
…
编 不……
第 23题 F 备用图 …D …过…P ………此…
云 ………
线
风 ………
…
…
九年级数学十二月月考试卷 第 8 页 (共 8 页)
2021—2022学年度第一学期月考试卷(十二月月考)
数学参考答案及评分标准
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1.B 2.D 3.C 4.A 5.A 6.C 7.C 8.B 9.A 10.D
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
11. y=-x2-1;12. =;13.2 10 2;14.(1)(-3,0)(2分)(2)k<0且 k≠-4(器3分)
三、(本大题 2 个小题,每小题 8 分,共 16 分)
15.解:(x-1)(x-2)=0 (4分) 辑
x 1 0或 x 2 0 .
x1 1, x2 2. (8分)
16.解:(1)如图所示 (4分) 编
(2)利用网格分别作 BC,AB 的垂直平分线交于点 P,
则点 P 为△ABC 外接圆的圆心. (8 分) F
四、(本大题 2 个小题,每小题 8 分D,共 16 分)17.解:(1)设该企业P从 2018年到 2020年利润的年平均增长率为 x.(1 分)根据题意得 3(1+x)2=4.32. (4 分)
解得 x1 =0.2=20%,x2 =-2.2(不合题意,舍去).
答:该企云业从 2018年到 2020年利润的年平均增长率为 20%.(6 分)(2)如果仍保持相同的年平均增长率,
那么该企业的 2021 年的利润为 4.32(1+20%)=5.184>5.
风答:该企业 2017 年的利润能超过 5 亿元 . (8 分)18.解:(1)由旋转的性质得,CD=CO,∠ACD=∠BCO.(1分)
∵∠ACB=60°,∴∠DCO=60°,
∴△OCD为等边三角形. (3分)
九年级数学十二月月考试卷 第 9 页 (共 8 页)
∴∠ODC=60°. (4分)
(2)由旋转的性质得,AD=OB=2. (5分)
∵△OCD为等边三角形,∴OD=OC=3 (6分)
∵∠BOC=150°,∠ODC=60°,
∴∠ADO=90°. (7分)
在 Rt△AOD中, AO= 13 . (8分)
五、(本大题 2 个小题,每小题 10 分,共 20 分) 器
19.解:如图,过点 A作 AE⊥BD于点 E,连接 AD.(2分)
∴AD=AB=5,
根据垂径定理,得 DE=BE, 辑
∴CE=BE﹣BC=DE﹣2. (4分)
根据勾股定理,得
AD2﹣DE2=AC2﹣CE2, 编
∴52﹣DE2=42﹣(DE﹣2)2,
13 F
解得 DE= . (8分)
4
∴CD=DE+CE=2DE﹣2P= 9. (10分)2 D20.解:(1)-24≤y≤1 (2分)(2)-1≤x≤0或 4≤x≤5 (6分)
(3)由题云意,y1=-m
2+4m-3,y2=-(m+1)2+4(m+1)-3
则 y1-y2=2m-3 (8分)
3
又 m< ,∴2m-3<0,即 y1<y2. (10分)
2
风六、(本题满分 12 分)21.(1)证明:如图,连接 OD. (1分)
∵AB为切线,∴OD⊥AB,∴∠ODB=90°.
∵∠ACB=90°,∴∠ABC+∠COD=180°.
九年级数学十二月月考试卷 第 10 页 (共 8 页)
∵∠AOD+∠COD=180°,∴∠AOD=∠ABC.(4分)
∵∠AOD=2∠ACD,∴∠ACD= 1∠ABC. (6分)
2
(2)解:在 Rt△ABC中,AB= 62 + 82 =10,
∵OC⊥CB,∴BC为切线,∴BD=BC=6,∴AD=4. (8分)
设⊙O的半径为 r,则 OD=OC=r,OA=8﹣r,
在 Rt△AOD中,r2+42=(8﹣r)2,解得 r=3,∴OC=3. (9分)
如图,连接 OB交 CD于 H. 器
∵OC=OD,BC=BD,∴OB垂直平分 CD. (10分)
在 Rt△OCB中,OB= 32 + 62 =3 5,
1
∵ OB CH= 1OC BC CH= 3×6,∴ = 6 5, 辑
2 2 3 5 5
12 5
∴CD=2CH= . (12分)
5
七、(本题满分 12 分) 编
1
22.解:(1)根据题意,得 R1=P(Q1-20)=(-2x+ 80F)[( x+30)-20]= -x2+20x+800(3分)2
R2=P(Q2-20)=(-2x+80)(45-20)= -50xD+2000 (5分)(2)当 1≤x≤20时,R1=-(x-10)2+900,
当 x=10时,R1的最大值为 900; (8分)
当 21≤x≤30时,R2=-50Px+2000.
R2的值随 x值的增大而减小,
当 x=21时云,R2的最大值是 950. (10分)∵950>900,
风∴在第 21天时,日销售利润最大,最大利润为 950元. (12分)八、(本题满分 14 分)
23.(1)把 A(3,0),B(-1,0)代入 y=-x2+bx+c,
解得 b=2,c=3.∴抛物线的解析式为 y=-x2+2x+3.(2分)
九年级数学十二月月考试卷 第 11 页 (共 8 页)
则 C点为(0,3).又 A(3,0),代入 y=kx+b1,
得 k=-1,b1=3. ∴直线 AC的解析式为 y=-x+3. (4分)
(2)当 P点与 B点重合时,连接 PC,此时 DP=DA.
则△ACP 的面积是△ACD面积的 2倍,即 P为(-1,0). (5分)
过 B点作 BP∥AC交抛物线于点 P,即为所求,
此时直线 BP的解析式为 y=-x-1. (6分)
与抛物线解析式 y=-x2+2x+3联立, 器
解得 x=-1,y=0;或者 x=4,y=-5.所以(4,-5)为所求.
综上,点 P的坐标为(-1,0)或(4,-5) (8分)
(3)由(1)可知,抛物线解析式为 y=-(x-1)2+4 辑
把 x=1代入直线 AC解析式 y=-x+3,
得 AC与抛物线对称轴的交点M(1,2),如右图所示.
则△MAB是等腰直角三角形,符合题意. 编
M点即为所求 Q点的一种情况. (10分)
当 Q点在 x轴下方时,设 Q为(1,m),mF<0.
因为线段 AQ绕 Q点顺时针旋转 90°得到线段 QA1,
过 A1作直线 DQ的垂线于PE点,则D△ADQ≌△QEA1. (11分)∴AD=QE=2,DQ=EA1=-m.∴A1(1-m,m-2). (12分)
∵点 A1恰云好落在抛物线 y=-x2+2x+3上,代入,解得 m=-3(舍去 m=2).∴Q(1,-3)综上,Q点坐标为(1,2)或(1,-3). (14分)
风【说明:以上解法不唯一,只要合理,均应给分】
九年级数学十二月月考试卷 第 12 页 (共 8 页)
同课章节目录
