2021-2022学年高中数学人教版A版(2019)选择性必修一3.2.2双曲线的简单几何性质 课件(共35张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.2.2双曲线的简单几何性质 课件(共35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:12:19 | ||
图片预览









文档简介
(共35张PPT)
3.2.2 双曲线的简单几何性质
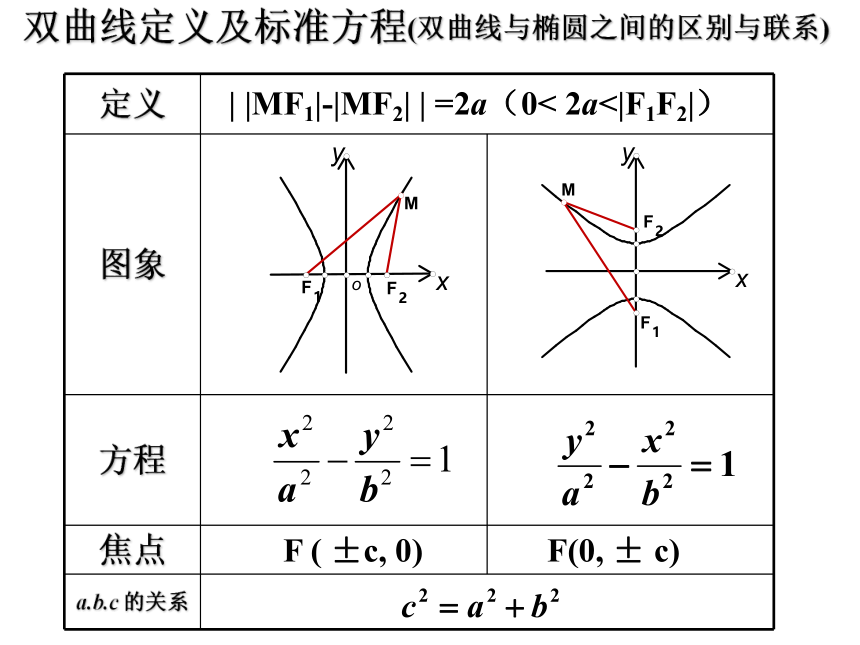
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0< 2a<|F1F2|)
F ( ±c, 0)
双曲线定义及标准方程
F(0, ± c)
(双曲线与椭圆之间的区别与联系)
椭圆 双曲线
4、双曲线与椭圆之间的区别与联系
1、方程
表示________。
2、方程
表示________。
焦点为(-5,0)(5,0)的双曲线的右支
一条射线
3、双曲线mx2+ny2=mn(n<0课堂练习
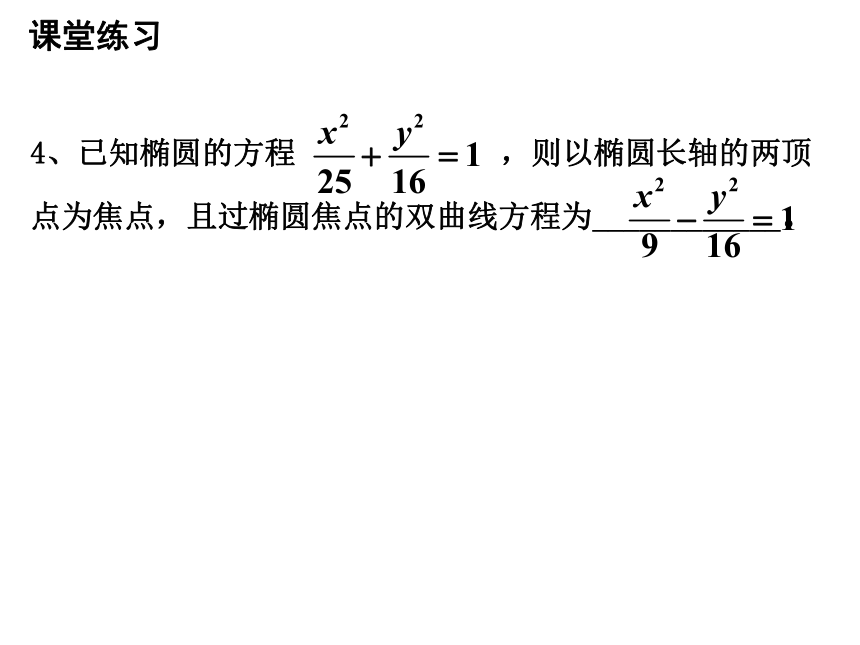
4、已知椭圆的方程 ,则以椭圆长轴的两顶点为焦点,且过椭圆焦点的双曲线方程为____________。
课堂练习
题
(舍去)
(待定系数法)
思考:方程mx2+ny2=1什么时候表示椭圆,
什么时候表示双曲线?
当mn<0时,表示双曲线
当m>0,n>0且m≠n时,表示椭圆
变题:若是mx2-ny2=1呢?
当mn>0时,表示双曲线
当m>0,n<0且m≠-n时,表示椭圆
一般地,若不知道焦点的位置,为了避开讨论,
双曲线的方程可设为:mx2+ny2=1(mn<0)
椭圆的方程可设为:mx2+ny2=1(m>0,n>0且m≠n)
例2、若方程 表示焦点在y轴的双曲线,
求m的取值范围.
变题1:若该方程表示双曲线,求m的取值范围。
m<1
m<1或m>2
变题2:若该方程表示的是椭圆,求m的取值范围。
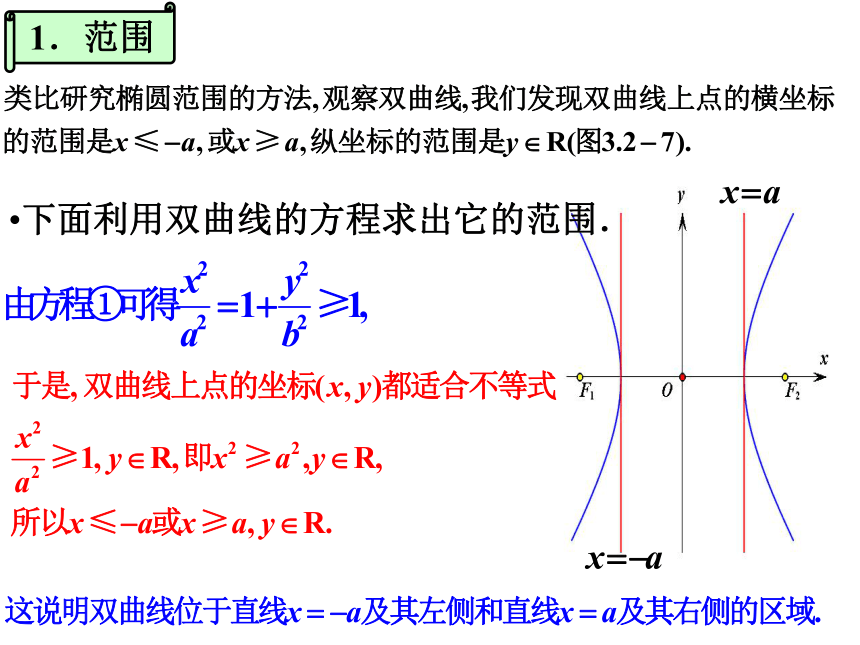
1.范围
下面利用双曲线的方程求出它的范围.
2.对称性
这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心双曲线的对称中心叫做双曲线的中心.
图3.2-8
3.顶点
图3.2-8
d
4.渐近线
d
实际上,双曲线与它的渐近线无限接近,但永不相交.
5.离心率
双曲线的离心率刻画了双曲线的“张口”大小.
思考
椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征?
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗?它与用离心率刻画“张口”大小有什么区别和联系?
例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(图3.2-10(1)).它的最小半径为12m,上口半径为13m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
图3.2-11
思考
将例5与椭圆一节中得例6比较,你有什么发现?
这就是椭圆和双曲线的第二定义.
图3.2-12
图3.2-12
c
b
a
a
b
c
记住这两个三角形
作业1
P127第4题
作业2
P128 第13题
3.2.2 双曲线的简单几何性质
定义
图象
方程
焦点
a.b.c 的关系
| |MF1|-|MF2| | =2a(0< 2a<|F1F2|)
F ( ±c, 0)
双曲线定义及标准方程
F(0, ± c)
(双曲线与椭圆之间的区别与联系)
椭圆 双曲线
4、双曲线与椭圆之间的区别与联系
1、方程
表示________。
2、方程
表示________。
焦点为(-5,0)(5,0)的双曲线的右支
一条射线
3、双曲线mx2+ny2=mn(n<0
4、已知椭圆的方程 ,则以椭圆长轴的两顶点为焦点,且过椭圆焦点的双曲线方程为____________。
课堂练习
题
(舍去)
(待定系数法)
思考:方程mx2+ny2=1什么时候表示椭圆,
什么时候表示双曲线?
当mn<0时,表示双曲线
当m>0,n>0且m≠n时,表示椭圆
变题:若是mx2-ny2=1呢?
当mn>0时,表示双曲线
当m>0,n<0且m≠-n时,表示椭圆
一般地,若不知道焦点的位置,为了避开讨论,
双曲线的方程可设为:mx2+ny2=1(mn<0)
椭圆的方程可设为:mx2+ny2=1(m>0,n>0且m≠n)
例2、若方程 表示焦点在y轴的双曲线,
求m的取值范围.
变题1:若该方程表示双曲线,求m的取值范围。
m<1
m<1或m>2
变题2:若该方程表示的是椭圆,求m的取值范围。
1.范围
下面利用双曲线的方程求出它的范围.
2.对称性
这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心双曲线的对称中心叫做双曲线的中心.
图3.2-8
3.顶点
图3.2-8
d
4.渐近线
d
实际上,双曲线与它的渐近线无限接近,但永不相交.
5.离心率
双曲线的离心率刻画了双曲线的“张口”大小.
思考
椭圆的离心率刻画了椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征?
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗?它与用离心率刻画“张口”大小有什么区别和联系?
例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(图3.2-10(1)).它的最小半径为12m,上口半径为13m,下口半径为25 m,高为55 m.试建立适当的坐标系,求出此双曲线的方程(精确到1m).
图3.2-11
思考
将例5与椭圆一节中得例6比较,你有什么发现?
这就是椭圆和双曲线的第二定义.
图3.2-12
图3.2-12
c
b
a
a
b
c
记住这两个三角形
作业1
P127第4题
作业2
P128 第13题
