2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.2抛物线的简单几何性质(2) 课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.2抛物线的简单几何性质(2) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
3.3.2 抛物线的简单几何性质(2)
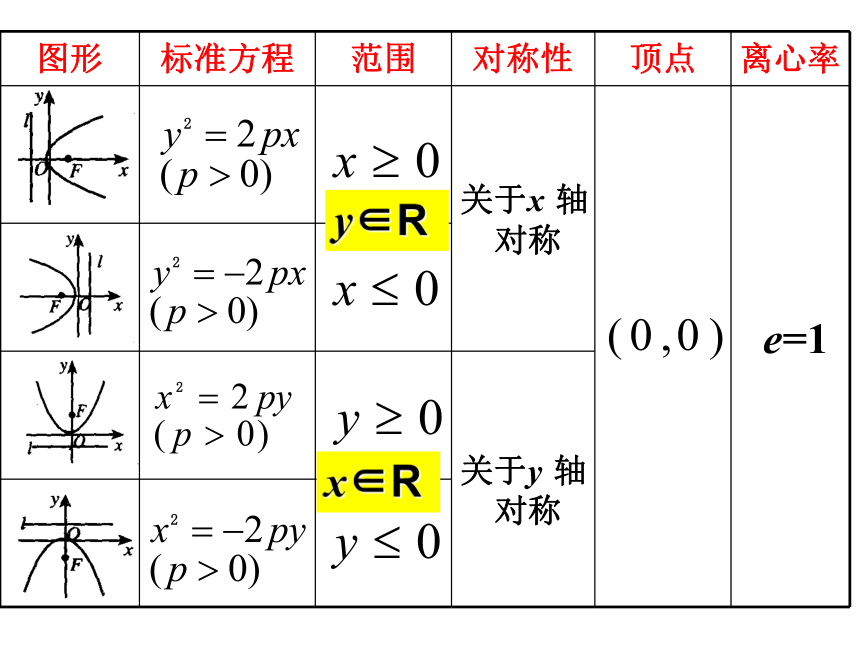
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称
关于y 轴
对称
e=1
y∈R
x∈R
抛物线的焦点弦的特征
(2)|AB|的最小值2p;(通径)
(3)以AB为直径的圆与准线相切;
若AB是抛物线y2=2px的任意一条焦点弦,且A(x1,y1)、B(x2,y2),直线AB的倾斜角为 , 则
(1)y1 y2=-p2,x1x2= ;
A
B
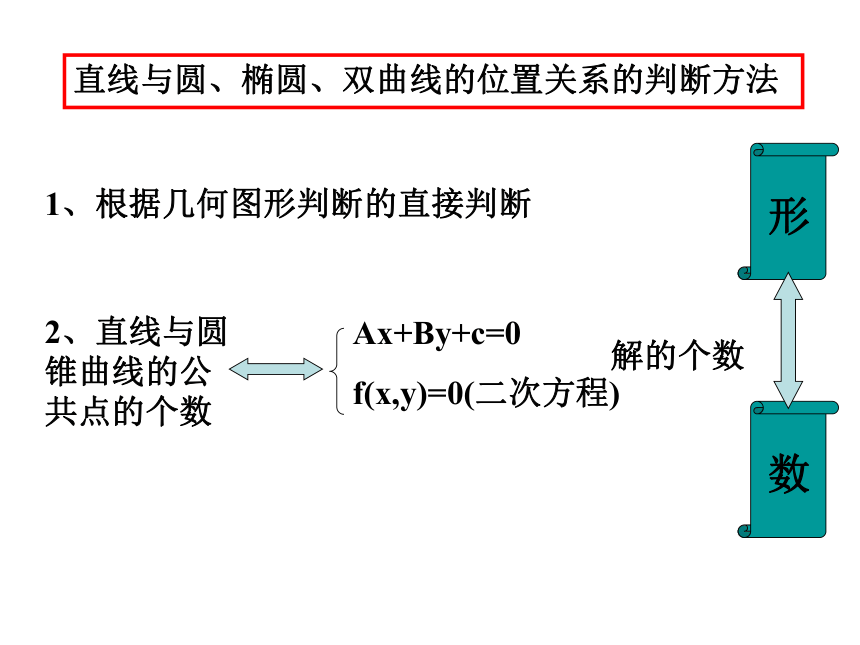
直线与圆、椭圆、双曲线的位置关系的判断方法
1、根据几何图形判断的直接判断
2、直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
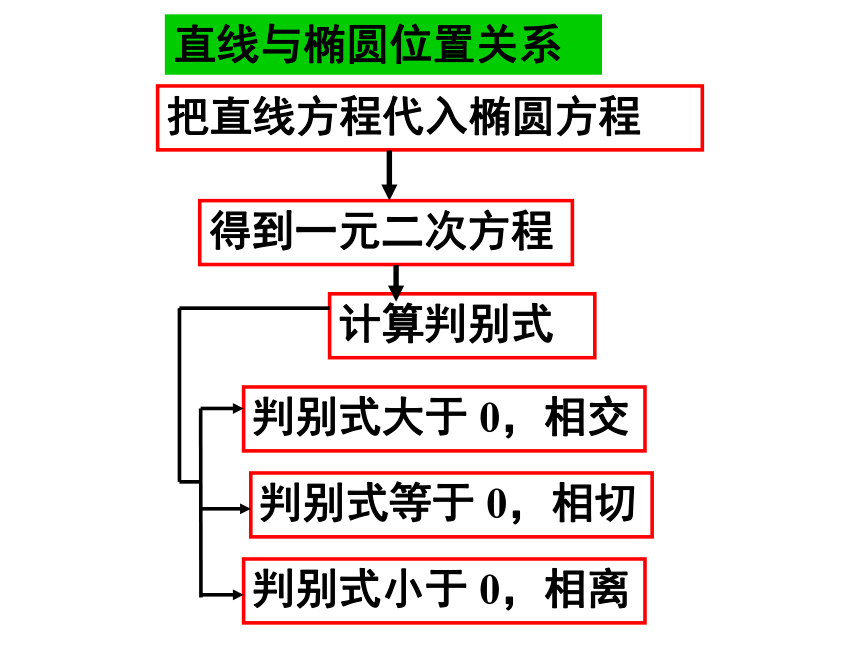
直线与椭圆位置关系
把直线方程代入椭圆方程
得到一元二次方程
计算判别式
判别式大于 0,相交
判别式等于 0,相切
判别式小于 0,相离
3.1.2 椭圆的简单几何性质(第2课时)
(专题研究 直线与椭圆的位置关系)
3.2.2 双曲线的简单几何性质(第2课时)
判断直线与双曲线位置关系
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的渐进线
平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
两个交点
一个交点
没有交点
探究新知
(1)有一个公共点
(2)两个公共交点
(3)没有公共点
F
x
1 直线和抛物线的位置关系有哪几种
y
例2:判断直线 y = 6与抛物线 y2 =4x的
位置关系及求交点坐标?
相交(9,6)
问题:直线与抛物线的对称轴平行时都有一个交点吗?
注意,当直线与抛物线的对称轴平行时有一个交点
x
y
O
探究新知
探究新知
探究新知
探究新知
判断直线与抛物线位置关系的操作程序:
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
总结:
(2条)
(4条)
变式一:把抛物线换成椭圆 结果如何?
(3条)
变式二:把抛物线换成双曲线 结果 如何?
练习:
直线和抛物线方程联立的方程组解的个数与位置关系
方程组两组解
两个交点
方程组没有解
没有交点
方程组一组解
一个交点
(2)若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.
(1)若消元得到二次方程,则
小结:
例6:
3.3.2 抛物线的简单几何性质(2)
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称
关于y 轴
对称
e=1
y∈R
x∈R
抛物线的焦点弦的特征
(2)|AB|的最小值2p;(通径)
(3)以AB为直径的圆与准线相切;
若AB是抛物线y2=2px的任意一条焦点弦,且A(x1,y1)、B(x2,y2),直线AB的倾斜角为 , 则
(1)y1 y2=-p2,x1x2= ;
A
B
直线与圆、椭圆、双曲线的位置关系的判断方法
1、根据几何图形判断的直接判断
2、直线与圆锥曲线的公共点的个数
Ax+By+c=0
f(x,y)=0(二次方程)
解的个数
形
数
直线与椭圆位置关系
把直线方程代入椭圆方程
得到一元二次方程
计算判别式
判别式大于 0,相交
判别式等于 0,相切
判别式小于 0,相离
3.1.2 椭圆的简单几何性质(第2课时)
(专题研究 直线与椭圆的位置关系)
3.2.2 双曲线的简单几何性质(第2课时)
判断直线与双曲线位置关系
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的渐进线
平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
两个交点
一个交点
没有交点
探究新知
(1)有一个公共点
(2)两个公共交点
(3)没有公共点
F
x
1 直线和抛物线的位置关系有哪几种
y
例2:判断直线 y = 6与抛物线 y2 =4x的
位置关系及求交点坐标?
相交(9,6)
问题:直线与抛物线的对称轴平行时都有一个交点吗?
注意,当直线与抛物线的对称轴平行时有一个交点
x
y
O
探究新知
探究新知
探究新知
探究新知
判断直线与抛物线位置关系的操作程序:
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
总结:
(2条)
(4条)
变式一:把抛物线换成椭圆 结果如何?
(3条)
变式二:把抛物线换成双曲线 结果 如何?
练习:
直线和抛物线方程联立的方程组解的个数与位置关系
方程组两组解
两个交点
方程组没有解
没有交点
方程组一组解
一个交点
(2)若消元得到一次方程,则方程组只有一组解,直线和抛物线的对称轴平行或重合,为相交关系.
(1)若消元得到二次方程,则
小结:
例6:
