2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.2抛物线的简单几何性质(1) 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.2抛物线的简单几何性质(1) 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
3.3.2 抛物线的简单几何性质(1)
一、复习
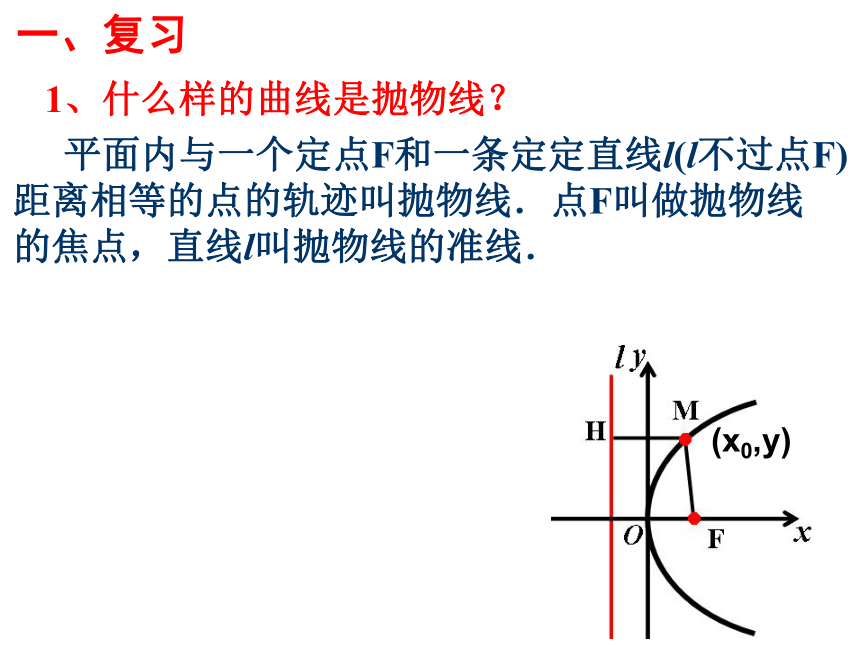
1、什么样的曲线是抛物线?
平面内与一个定点F和一条定定直线l(l不过点F)距离相等的点的轨迹叫抛物线.点F叫做抛物线的焦点,直线l叫抛物线的准线.
(x0,y)
图形 标准方程 焦点坐标 准线方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
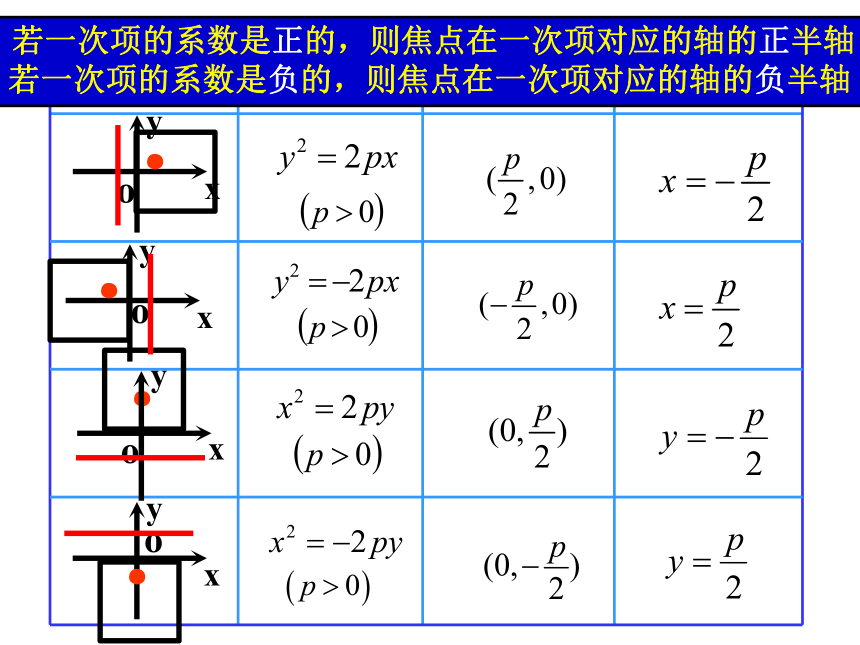
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
抛物线的简单几何性质
问题:
已知抛物线C的顶点在坐标原点,坐标轴为对称轴,它被直线x=2截得的弦长 ,求抛物线的方程.
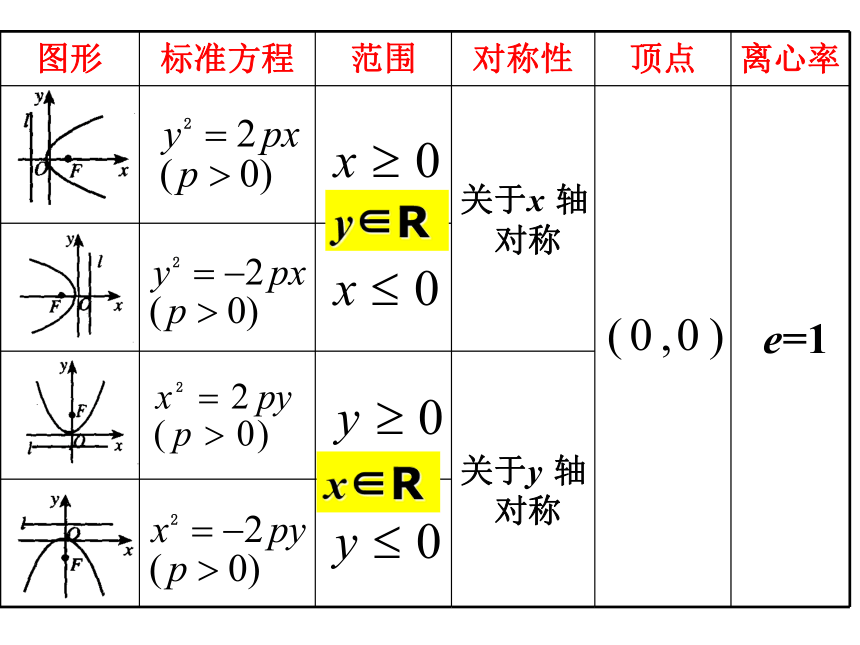
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称
关于y 轴
对称
e=1
y∈R
x∈R
问题:
已知抛物线C的顶点在坐标原点,坐标轴为对称轴,它被直线x=2截得的弦长 ,求抛物线的方程.
x
y
o
·
2
l
A
B
抛物线方程为 : y2=4x
解:依题意可设抛物线方程为 y2=2px (p>0)
则由对称性知,点A坐标为:
x
y
O
F
A
B
B’
A’
x
y
O
F
A
B
B’
A’
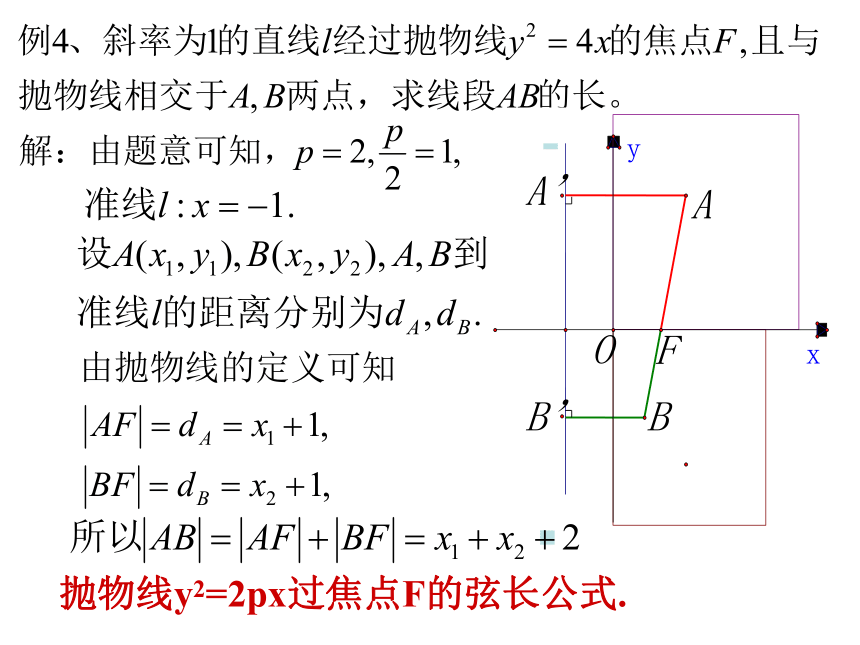
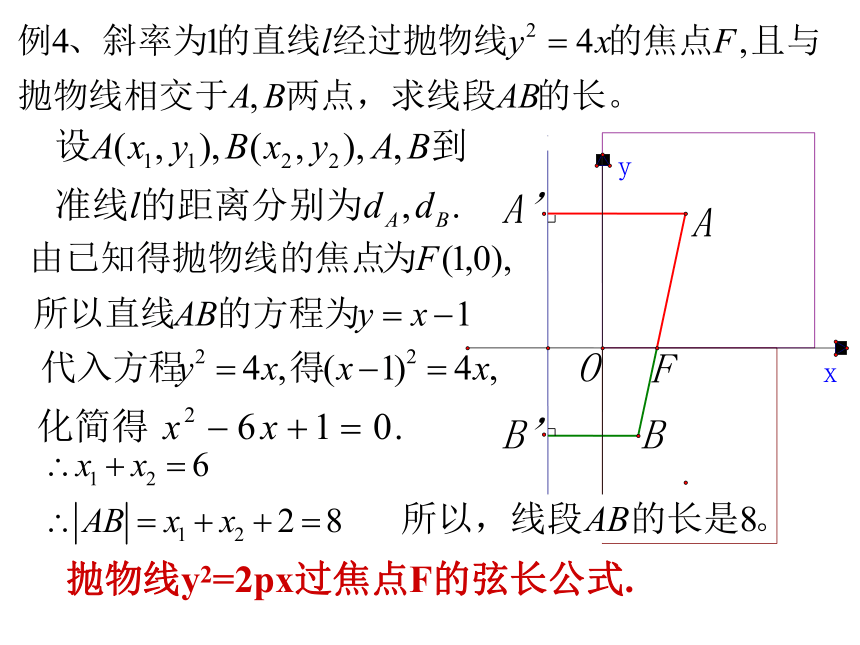
抛物线y2=2px过焦点F的弦长公式.
x
y
O
F
A
B
B’
A’
抛物线y2=2px过焦点F的弦长公式.
抛物线y2=2px(p>0)的焦点弦长:
方法1:设M是焦点弦的中点,
且点M 的横坐标为x0 ,
F
A
l
E
O
x
y
·
·
B
·
H
探究:以AB为直径的圆与
这抛物线的准线的位置
关系
则点M 到准线l的距离d=
·M
探究方法2: 过抛物线y2=2px的焦点F任作一条直线m,交这抛物线于A、B两点,则以AB为直径的圆和这抛物线的准线相切.
思考:你能求出|AB|的最小值吗?
所以EH是以AB为直径的圆E的
半径,且EH⊥l,因而圆E和准线l 相切.
解:设AB的中点为E,过A、E、B
分别向准线l引垂线AD,EH,BC,
垂足为D、H、C,
则| AF |=|AD|,| BF |=|BC|
∴|AB|=|AF|+|BF|
=|AD|+|BC|
=2|EH|
y2=2px
x
y
o
·
F
l
A
B
过焦点且垂直于对称轴的直线被抛物线截得的线段AB叫做抛物线的通径,
长为2p
p越大,开口越大
抛物线开口大小 :
课本P72 练习2.
抛物线的焦点弦的特征
(1)|AB|的最小值2p;(通径)
(3)|AB|=x1+x2+p;(焦点在x轴正半轴)
(4)以AB为直径的圆与准线相切;
若AB是抛物线y2=2px的任意一条焦点弦,且
A(x1,y1)、B(x2,y2),则
(5)y1 y2=-p2,x1x2= ;
例5、过抛物线焦点F的直线交抛物线于A,B两点,通过
点A和抛物线顶点的直线交抛物线的准线于点D,求证:
直线DB平行于抛物线的对称轴。
O
A
F
B
D
x
y
O
A
F
B
D
x
y
练习:
D
B
C
课堂小结:
1、抛物线的简单几何性质
2、抛物线的焦点弦问题
作业P136
3.3.2 抛物线的简单几何性质(1)
一、复习
1、什么样的曲线是抛物线?
平面内与一个定点F和一条定定直线l(l不过点F)距离相等的点的轨迹叫抛物线.点F叫做抛物线的焦点,直线l叫抛物线的准线.
(x0,y)
图形 标准方程 焦点坐标 准线方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
抛物线的简单几何性质
问题:
已知抛物线C的顶点在坐标原点,坐标轴为对称轴,它被直线x=2截得的弦长 ,求抛物线的方程.
图形 标准方程 范围 对称性 顶点 离心率
关于x 轴
对称
关于y 轴
对称
e=1
y∈R
x∈R
问题:
已知抛物线C的顶点在坐标原点,坐标轴为对称轴,它被直线x=2截得的弦长 ,求抛物线的方程.
x
y
o
·
2
l
A
B
抛物线方程为 : y2=4x
解:依题意可设抛物线方程为 y2=2px (p>0)
则由对称性知,点A坐标为:
x
y
O
F
A
B
B’
A’
x
y
O
F
A
B
B’
A’
抛物线y2=2px过焦点F的弦长公式.
x
y
O
F
A
B
B’
A’
抛物线y2=2px过焦点F的弦长公式.
抛物线y2=2px(p>0)的焦点弦长:
方法1:设M是焦点弦的中点,
且点M 的横坐标为x0 ,
F
A
l
E
O
x
y
·
·
B
·
H
探究:以AB为直径的圆与
这抛物线的准线的位置
关系
则点M 到准线l的距离d=
·M
探究方法2: 过抛物线y2=2px的焦点F任作一条直线m,交这抛物线于A、B两点,则以AB为直径的圆和这抛物线的准线相切.
思考:你能求出|AB|的最小值吗?
所以EH是以AB为直径的圆E的
半径,且EH⊥l,因而圆E和准线l 相切.
解:设AB的中点为E,过A、E、B
分别向准线l引垂线AD,EH,BC,
垂足为D、H、C,
则| AF |=|AD|,| BF |=|BC|
∴|AB|=|AF|+|BF|
=|AD|+|BC|
=2|EH|
y2=2px
x
y
o
·
F
l
A
B
过焦点且垂直于对称轴的直线被抛物线截得的线段AB叫做抛物线的通径,
长为2p
p越大,开口越大
抛物线开口大小 :
课本P72 练习2.
抛物线的焦点弦的特征
(1)|AB|的最小值2p;(通径)
(3)|AB|=x1+x2+p;(焦点在x轴正半轴)
(4)以AB为直径的圆与准线相切;
若AB是抛物线y2=2px的任意一条焦点弦,且
A(x1,y1)、B(x2,y2),则
(5)y1 y2=-p2,x1x2= ;
例5、过抛物线焦点F的直线交抛物线于A,B两点,通过
点A和抛物线顶点的直线交抛物线的准线于点D,求证:
直线DB平行于抛物线的对称轴。
O
A
F
B
D
x
y
O
A
F
B
D
x
y
练习:
D
B
C
课堂小结:
1、抛物线的简单几何性质
2、抛物线的焦点弦问题
作业P136
