2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.1抛物线及其标准方程 课件(共30张PPT)
文档属性
| 名称 | 2021-2022学年高中数学人教版A版(2019)选择性必修一3.3.1抛物线及其标准方程 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 894.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:15:04 | ||
图片预览






文档简介
(共30张PPT)
3.3.1 抛物线及其标准方程
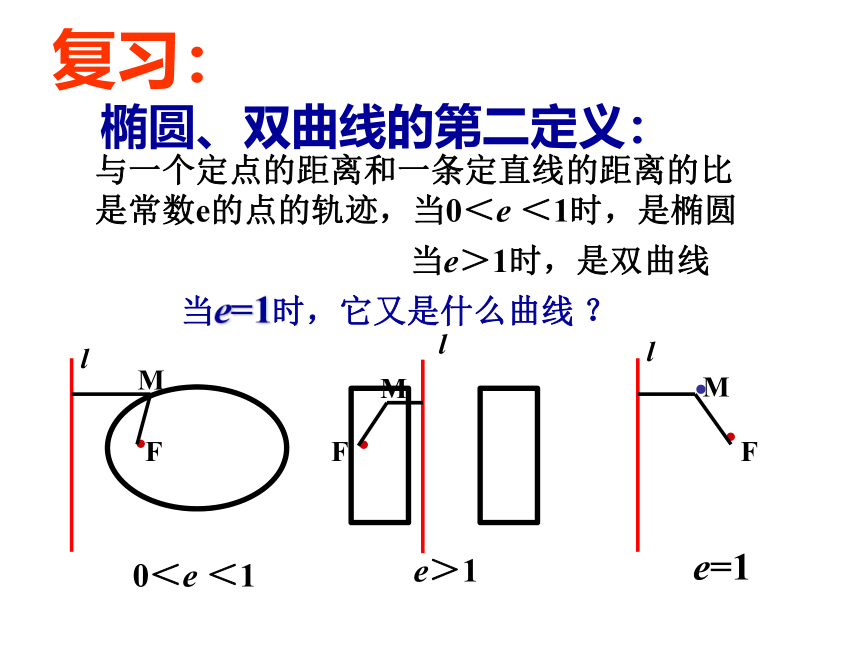
复习:
椭圆、双曲线的第二定义:
与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当0<e <1时,是椭圆
·
M
F
l
0<e <1
l
F
·
M
e>1
·
F
M
l
·
e=1
当e>1时,是双曲线
当e=1时,它又是什么曲线 ?
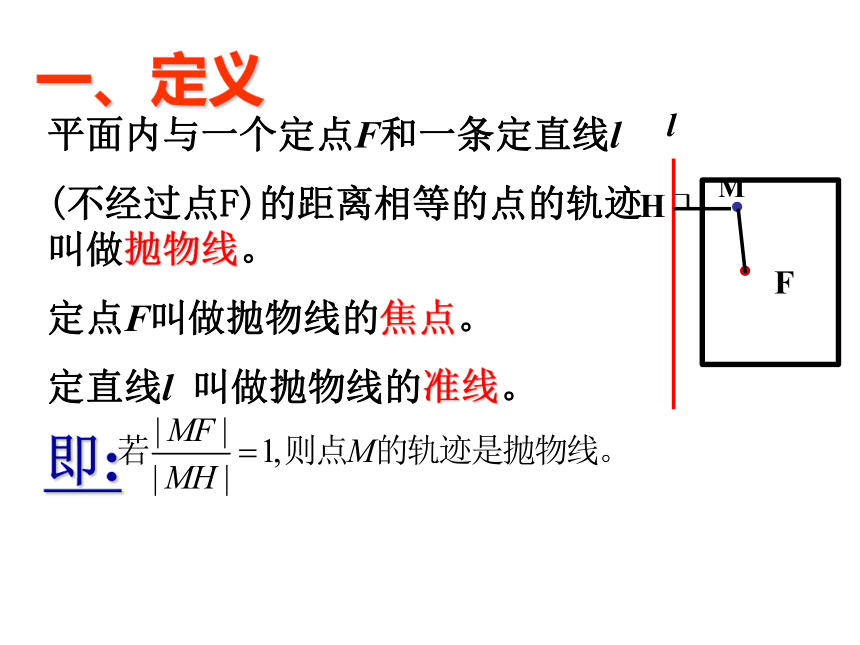
平面内与一个定点F和一条定直线l
(不经过点F)的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义
即:
·
·
F
M
l
H
二、抛物线的标准方程
·
·
F
M
l
H
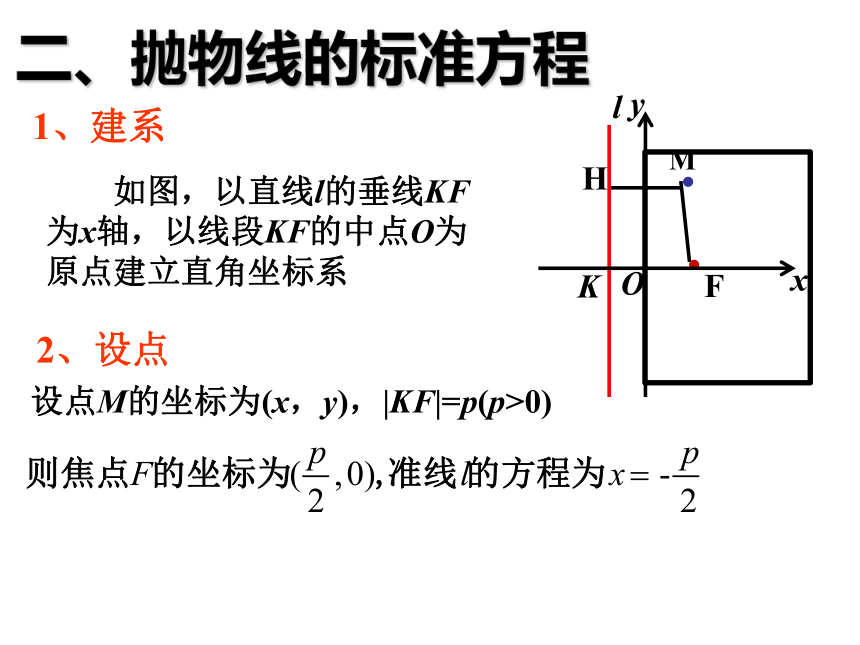
1、建系
O
K
x
y
如图,以直线l的垂线KF
为x轴,以线段KF的中点O为
原点建立直角坐标系
2、设点
设点M的坐标为(x,y),|KF|=p(p>0)
二、抛物线的标准方程
·
·
F
M
l
H
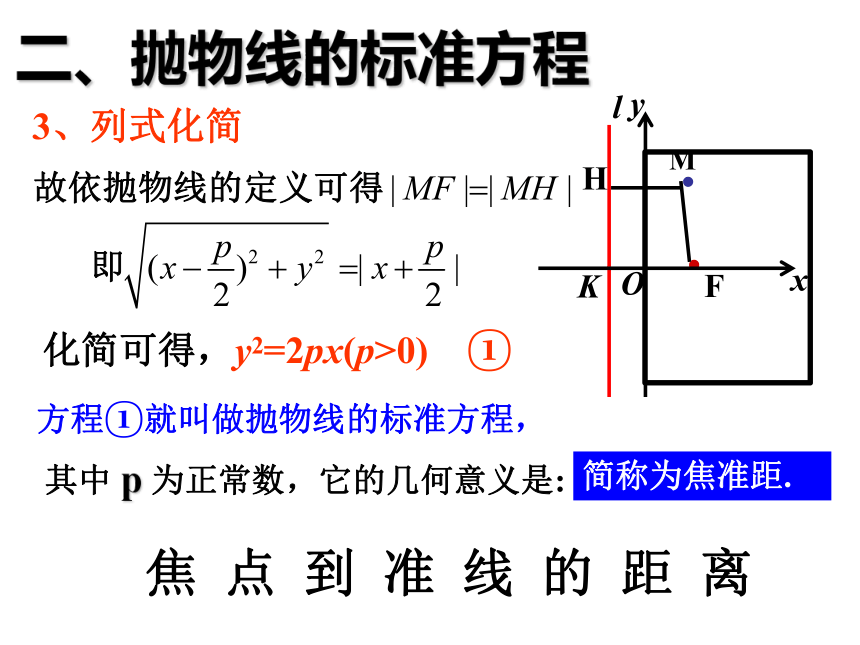
3、列式化简
O
K
x
y
化简可得,y2=2px(p>0) ①
方程①就叫做抛物线的标准方程,
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
简称为焦准距.
二、抛物线的标准方程
·
·
F
M
l
H
O
K
x
y
y2=2px(p>0)
上述方程表示焦点在x轴的正半轴,
对称轴为x轴的一条抛物线,
其中,p为焦点到准线的距离,
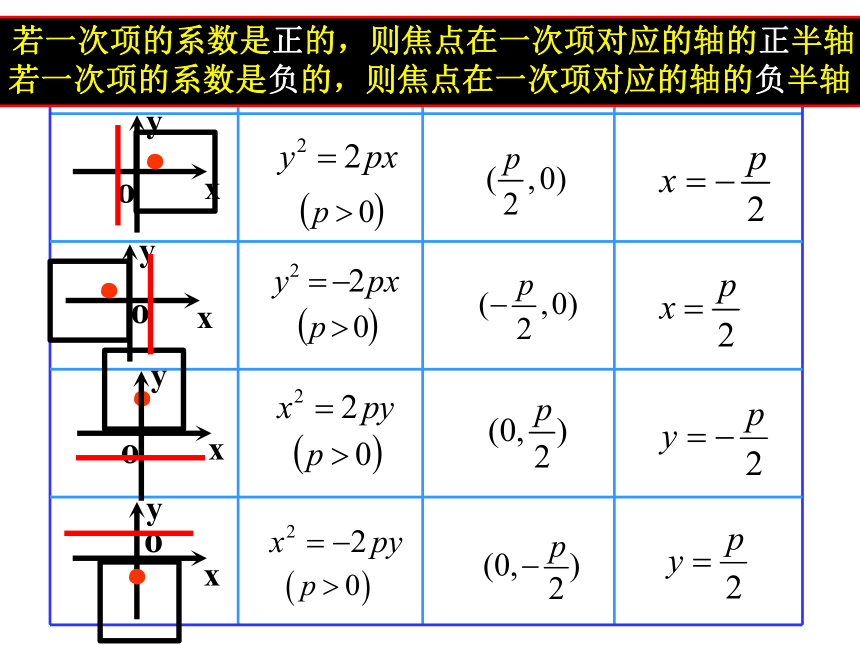
图形 标准方程 焦点坐标 准线方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
例1、求下列抛物线的焦点坐标及准线方程:
(1)y2 = 6x;(2)x2=-2y;
p>0
练习.求满足下列条件的抛物线的标准方程:
(1)焦点为(0,-2); (2)准线为y=-1;
(3)焦点到准线的距离为4;
(1)∵抛物线的焦点为在y轴负半轴 , P=4,
∴ x2=-8y
(2) ∵ 抛物线的焦点为在y轴正半轴, P=2,
∴ x2=4y
(3) ∵抛物线的焦点在坐标轴上 P=4 ,
∴ y2=±8x 或 x2=±8y
练习、1.求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2) y = 2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,-2)
y=2
作业:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是 ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =±4x或 x2 =±4y
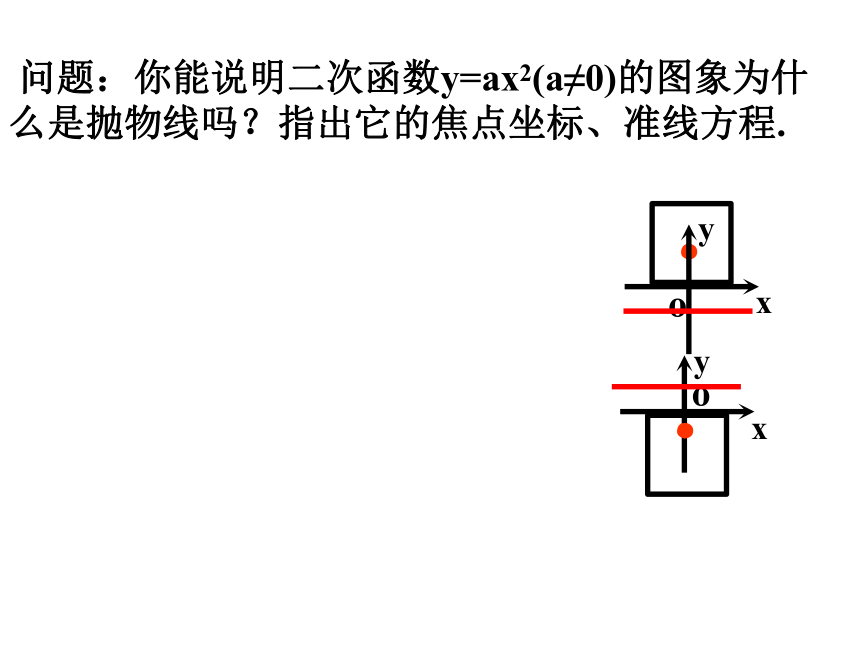
问题:你能说明二次函数y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程.
y
x
o
﹒
﹒
y
x
o
3.列抛物线y2=ax(a≠0)的焦点坐标: ,
准线方程: .
例2.一种卫星接收天线的轴截面如图所示,卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.已知接收天线的口径(直径)为4.8m,深度为1m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标.
方程:y2=5.76x
焦点:(1.44,0)
x
y
O
A
(0.5,2.4)
例2.求过点A(-3,2)的抛物线的标准方程.
.
A
O
y
x
解:(1)当抛物线的焦点在 y 轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
(2)当焦点在 x 轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y 或y2 = x
变式练习:已知抛物线的焦点在 x 轴上,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的标准方程.
解:因为是焦点在 x 轴上且过M点的抛物线,所以设标准方程为
由抛物线的定义知 -(-3)=5 即p=4.
所以所求抛物线标准方程为y2 = -8x
y2=-2px(p>0)
数形结合,用定义转化条件!
思考: 一般情况
思考:M是抛物线y2 = 2px(p>0)上一点,若点
M 的横坐标为x0,则点M到焦点的距离是
————————————
x0 + —
2
p
O
y
x
.
F
M
.
这就是抛物线的焦半径公式!
2. 若抛物线y2=8x上一点M到原点的距离 等于点M到准线的距离则点M的坐标是_________.
补充1. 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小 1,求点M的轨迹方程.
解:如图,设点M的坐标为(x,y),
依题意可知点M与点F的距离等于它到直线x+4=0的距离,根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线.
∵焦点在x轴的正半轴上,
∴点M的轨迹方程为:y2=16x
l
l’
M
x
O
y
F
(3).动点P到点A(0,2)的距离比到直线l:y=-4的距离小2,则动点P的轨迹方程为________
x2=8y
4. 过抛物线y2=4x的焦点F作直线l,交抛物线于A、B两点,求线段AB的中点M的轨迹方程.
x
F
O
y
M
B
A
故点M的轨迹的方程为:
当线段PQ的斜率不存在时,线段PQ中点为焦点F(1,0),满足此式。
例4.已知定点A(3,2)和抛物线y2=2x, F是抛物线焦点,试在抛物线上求一点P,使 PA与PF的 距离之和最小,并求出这个最小值.
练习巩固
作业:3.3.2 抛物线的简单几何性质(第2课时)例题2(1)
小 结 :
1、抛物线的定义,标准方程类型与图象的对应
关系以及判断方法
2、抛物线的定义、标准方程和它的焦点、
准线、方程.
3、注重数形结合的思想。
准线方程
焦点坐标
标准方程
焦点位置
图
形
3. 不同位置的抛物线
x轴的
正方向
x轴的
负方向
y轴的
正方向
y轴的
负方向
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
3.3.1 抛物线及其标准方程
复习:
椭圆、双曲线的第二定义:
与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹,当0<e <1时,是椭圆
·
M
F
l
0<e <1
l
F
·
M
e>1
·
F
M
l
·
e=1
当e>1时,是双曲线
当e=1时,它又是什么曲线 ?
平面内与一个定点F和一条定直线l
(不经过点F)的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义
即:
·
·
F
M
l
H
二、抛物线的标准方程
·
·
F
M
l
H
1、建系
O
K
x
y
如图,以直线l的垂线KF
为x轴,以线段KF的中点O为
原点建立直角坐标系
2、设点
设点M的坐标为(x,y),|KF|=p(p>0)
二、抛物线的标准方程
·
·
F
M
l
H
3、列式化简
O
K
x
y
化简可得,y2=2px(p>0) ①
方程①就叫做抛物线的标准方程,
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
简称为焦准距.
二、抛物线的标准方程
·
·
F
M
l
H
O
K
x
y
y2=2px(p>0)
上述方程表示焦点在x轴的正半轴,
对称轴为x轴的一条抛物线,
其中,p为焦点到准线的距离,
图形 标准方程 焦点坐标 准线方程
y
x
o
﹒
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
例1、求下列抛物线的焦点坐标及准线方程:
(1)y2 = 6x;(2)x2=-2y;
p>0
练习.求满足下列条件的抛物线的标准方程:
(1)焦点为(0,-2); (2)准线为y=-1;
(3)焦点到准线的距离为4;
(1)∵抛物线的焦点为在y轴负半轴 , P=4,
∴ x2=-8y
(2) ∵ 抛物线的焦点为在y轴正半轴, P=2,
∴ x2=4y
(3) ∵抛物线的焦点在坐标轴上 P=4 ,
∴ y2=±8x 或 x2=±8y
练习、1.求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2) y = 2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1)
(2)
(3)
(4)
(5,0)
x= -5
(0,-2)
y=2
作业:
1、根据下列条件,写出抛物线的标准方程:
(1)焦点是F(3,0);
(2)准线方程 是 ;
(3)焦点到准线的距离是2。
y2 =12x
y2 =x
y2 =±4x或 x2 =±4y
问题:你能说明二次函数y=ax2(a≠0)的图象为什么是抛物线吗?指出它的焦点坐标、准线方程.
y
x
o
﹒
﹒
y
x
o
3.列抛物线y2=ax(a≠0)的焦点坐标: ,
准线方程: .
例2.一种卫星接收天线的轴截面如图所示,卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处.已知接收天线的口径(直径)为4.8m,深度为1m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标.
方程:y2=5.76x
焦点:(1.44,0)
x
y
O
A
(0.5,2.4)
例2.求过点A(-3,2)的抛物线的标准方程.
.
A
O
y
x
解:(1)当抛物线的焦点在 y 轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p=
(2)当焦点在 x 轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y 或y2 = x
变式练习:已知抛物线的焦点在 x 轴上,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的标准方程.
解:因为是焦点在 x 轴上且过M点的抛物线,所以设标准方程为
由抛物线的定义知 -(-3)=5 即p=4.
所以所求抛物线标准方程为y2 = -8x
y2=-2px(p>0)
数形结合,用定义转化条件!
思考: 一般情况
思考:M是抛物线y2 = 2px(p>0)上一点,若点
M 的横坐标为x0,则点M到焦点的距离是
————————————
x0 + —
2
p
O
y
x
.
F
M
.
这就是抛物线的焦半径公式!
2. 若抛物线y2=8x上一点M到原点的距离 等于点M到准线的距离则点M的坐标是_________.
补充1. 点M与点F(4,0)的距离比它到直线l:x+5=0的距离小 1,求点M的轨迹方程.
解:如图,设点M的坐标为(x,y),
依题意可知点M与点F的距离等于它到直线x+4=0的距离,根据抛物线的定义,点M的轨迹是以F(4,0)为焦点的抛物线.
∵焦点在x轴的正半轴上,
∴点M的轨迹方程为:y2=16x
l
l’
M
x
O
y
F
(3).动点P到点A(0,2)的距离比到直线l:y=-4的距离小2,则动点P的轨迹方程为________
x2=8y
4. 过抛物线y2=4x的焦点F作直线l,交抛物线于A、B两点,求线段AB的中点M的轨迹方程.
x
F
O
y
M
B
A
故点M的轨迹的方程为:
当线段PQ的斜率不存在时,线段PQ中点为焦点F(1,0),满足此式。
例4.已知定点A(3,2)和抛物线y2=2x, F是抛物线焦点,试在抛物线上求一点P,使 PA与PF的 距离之和最小,并求出这个最小值.
练习巩固
作业:3.3.2 抛物线的简单几何性质(第2课时)例题2(1)
小 结 :
1、抛物线的定义,标准方程类型与图象的对应
关系以及判断方法
2、抛物线的定义、标准方程和它的焦点、
准线、方程.
3、注重数形结合的思想。
准线方程
焦点坐标
标准方程
焦点位置
图
形
3. 不同位置的抛物线
x轴的
正方向
x轴的
负方向
y轴的
正方向
y轴的
负方向
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
若一次项的系数是正的,则焦点在一次项对应的轴的正半轴
若一次项的系数是负的,则焦点在一次项对应的轴的负半轴
