2021年沪科版数学七年级上册 1.6 有理数的乘方(2) 课件(20张)
文档属性
| 名称 | 2021年沪科版数学七年级上册 1.6 有理数的乘方(2) 课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 669.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 21:47:00 | ||
图片预览







文档简介
(共20张PPT)
1.6 有理数的乘方
回顾 & 思考
有理数乘法(积的符号的确定):
积的符号是由负因数的个数决定
几个有理数相乘
口诀:偶为正,
奇为负
小故事:很久以前,印度的舍罕国王和西方国际象棋的发明人西塞·班·达依尔下棋,国王说:“你发明了这么有趣的象棋,我一定要重赏你,你想要什么尽管开口好了,我都会满足你的要求。”西塞说我想要的不过是一点米,在我的棋盘的
第一格放入一粒米,在第
二格放入第一格米的数量
的2倍,在第三格放入第二
格米的数量2倍……像这样
一直放到第64格就可以。
创设 & 情境
创设 & 情境
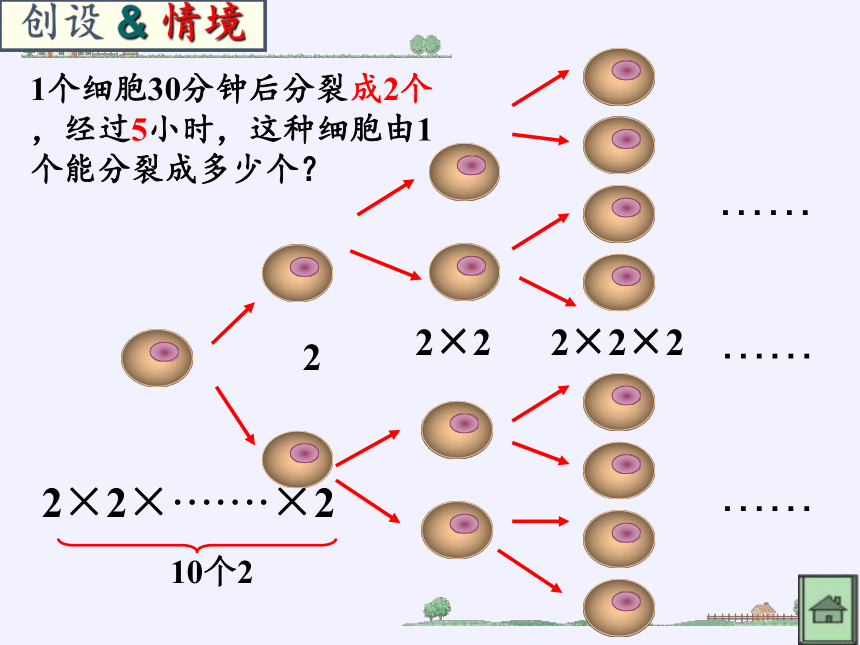
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2
10个2
……
……
……
5
5
5
5
5
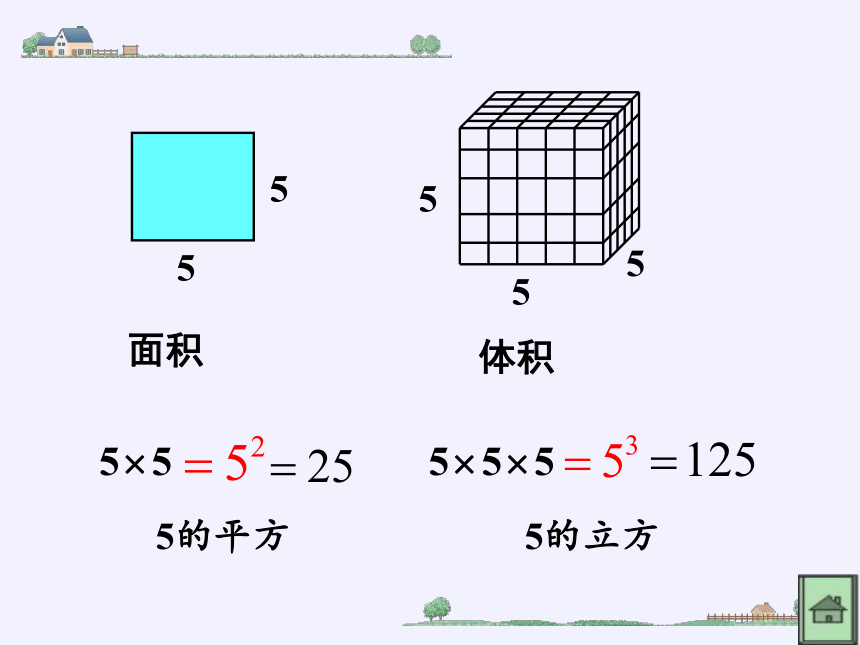
5的平方
5的立方
面积
体积
记作 210
a . a .… .a . a . a . a . a
n个a
求n个相同因数a的积的运算叫做乘方
记作 an
2×2×·······×2×2
10个2
a
n
a
n
读作:a的n次方或a的n次幂
指数
底数
幂
.
(-3)5
例1:1. (-3) ×(-3) ×(-3) ×(-3) ×(-3)
可以记为___
2.在(-5)2中,底数是____,指数是____.
3.在-53中,底数是____,指数是____.
-5
2
5
3
学以致用
议一议
-32 读作 32的相反数,
(-3)2 读作-3的平方
-32= -3×3 = -9
(-3)2 = (-3)×(-3 ) = 9
-32与(-3)2 有什么不同?结果相等吗?
与 有什么不同?结果相等吗?
学以致用
例2. 计算:
53 (2) (-3)4
解:(1) 53=
(2) (-3)4
(4)-34
(4) -34
5×5×5
=125
=(-3) × (-3) × (-3) × (-3)
=81
=-3×3×3×3
=-81
探索 & 交流
观察例2的结果,你能发现什么规律 小组讨论.
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数
偶为正,奇为负
小结 & 练习
运算 加 减 乘 除 乘方
结果 和 差 积 商
幂
求n个相同因数a的积的运算
乘方
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.
偶为正,奇为负
做一做
(1)在64中,底数是___,指数是____;
(3)在(-6)5中,底数是 ___, 指数是______;
一、写出下列各幂的底数与指数:
-6
4
a
4
6
5
(2)在a4中,底数是___,指数是____;
(4)在-25中,底数是____,指数是____;
2
5
二、如果:x2=64,x是几?x3=64,x是几?
答:如果:x2=64,x是8或-8;
小结 & 练习
x3=64,x是4。
想一想
三、(-1) n 当n偶数时,结果为___
当n奇数时,结果为___
小结 & 练习
1
-1
考考你
一个数的平方为16,这个数是________
一个数的平方是0,这个数是________
一个数的平方为它本身,这个数是_______
一个数的立方为它本身,这个数是________
小结 & 练习
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
这样捏合到第 次后可拉出128根面条。
生活与数学(一)
7
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?
≈
≈
异想天开
生活与数学(二)
这张纸对折30次后能超过珠穆朗玛峰吗?
有一张厚度是0.1毫米的纸,将它对折1 次后,厚度为2×0.1毫米。
(1)对折2次后,厚度为多少毫米?
(2)对折30次后,厚度为多少毫米?
1次
2次
30次
巴衣老爷说:你能每天给我10元钱,一共给我20年吗?阿凡提说:尊敬的巴衣老爷,如果你能第一天给我1毛钱,第二天给我2毛钱,第三天给我4毛钱,以此类推,一直给20天,那我就答应你的要求!巴衣老爷眼珠子一转说:那好吧!亲爱的同学们:你知道阿凡提和巴衣老爷谁得到的钱多?
乘方的故事
谢 谢
1.6 有理数的乘方
回顾 & 思考
有理数乘法(积的符号的确定):
积的符号是由负因数的个数决定
几个有理数相乘
口诀:偶为正,
奇为负
小故事:很久以前,印度的舍罕国王和西方国际象棋的发明人西塞·班·达依尔下棋,国王说:“你发明了这么有趣的象棋,我一定要重赏你,你想要什么尽管开口好了,我都会满足你的要求。”西塞说我想要的不过是一点米,在我的棋盘的
第一格放入一粒米,在第
二格放入第一格米的数量
的2倍,在第三格放入第二
格米的数量2倍……像这样
一直放到第64格就可以。
创设 & 情境
创设 & 情境
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2
10个2
……
……
……
5
5
5
5
5
5的平方
5的立方
面积
体积
记作 210
a . a .… .a . a . a . a . a
n个a
求n个相同因数a的积的运算叫做乘方
记作 an
2×2×·······×2×2
10个2
a
n
a
n
读作:a的n次方或a的n次幂
指数
底数
幂
.
(-3)5
例1:1. (-3) ×(-3) ×(-3) ×(-3) ×(-3)
可以记为___
2.在(-5)2中,底数是____,指数是____.
3.在-53中,底数是____,指数是____.
-5
2
5
3
学以致用
议一议
-32 读作 32的相反数,
(-3)2 读作-3的平方
-32= -3×3 = -9
(-3)2 = (-3)×(-3 ) = 9
-32与(-3)2 有什么不同?结果相等吗?
与 有什么不同?结果相等吗?
学以致用
例2. 计算:
53 (2) (-3)4
解:(1) 53=
(2) (-3)4
(4)-34
(4) -34
5×5×5
=125
=(-3) × (-3) × (-3) × (-3)
=81
=-3×3×3×3
=-81
探索 & 交流
观察例2的结果,你能发现什么规律 小组讨论.
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数
偶为正,奇为负
小结 & 练习
运算 加 减 乘 除 乘方
结果 和 差 积 商
幂
求n个相同因数a的积的运算
乘方
正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.
偶为正,奇为负
做一做
(1)在64中,底数是___,指数是____;
(3)在(-6)5中,底数是 ___, 指数是______;
一、写出下列各幂的底数与指数:
-6
4
a
4
6
5
(2)在a4中,底数是___,指数是____;
(4)在-25中,底数是____,指数是____;
2
5
二、如果:x2=64,x是几?x3=64,x是几?
答:如果:x2=64,x是8或-8;
小结 & 练习
x3=64,x是4。
想一想
三、(-1) n 当n偶数时,结果为___
当n奇数时,结果为___
小结 & 练习
1
-1
考考你
一个数的平方为16,这个数是________
一个数的平方是0,这个数是________
一个数的平方为它本身,这个数是_______
一个数的立方为它本身,这个数是________
小结 & 练习
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
这样捏合到第 次后可拉出128根面条。
生活与数学(一)
7
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?
≈
≈
异想天开
生活与数学(二)
这张纸对折30次后能超过珠穆朗玛峰吗?
有一张厚度是0.1毫米的纸,将它对折1 次后,厚度为2×0.1毫米。
(1)对折2次后,厚度为多少毫米?
(2)对折30次后,厚度为多少毫米?
1次
2次
30次
巴衣老爷说:你能每天给我10元钱,一共给我20年吗?阿凡提说:尊敬的巴衣老爷,如果你能第一天给我1毛钱,第二天给我2毛钱,第三天给我4毛钱,以此类推,一直给20天,那我就答应你的要求!巴衣老爷眼珠子一转说:那好吧!亲爱的同学们:你知道阿凡提和巴衣老爷谁得到的钱多?
乘方的故事
谢 谢
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
