黑龙江省绥化市第九中学2013届高三第二次月考理科数学试题
文档属性
| 名称 | 黑龙江省绥化市第九中学2013届高三第二次月考理科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-22 07:42:58 | ||
图片预览




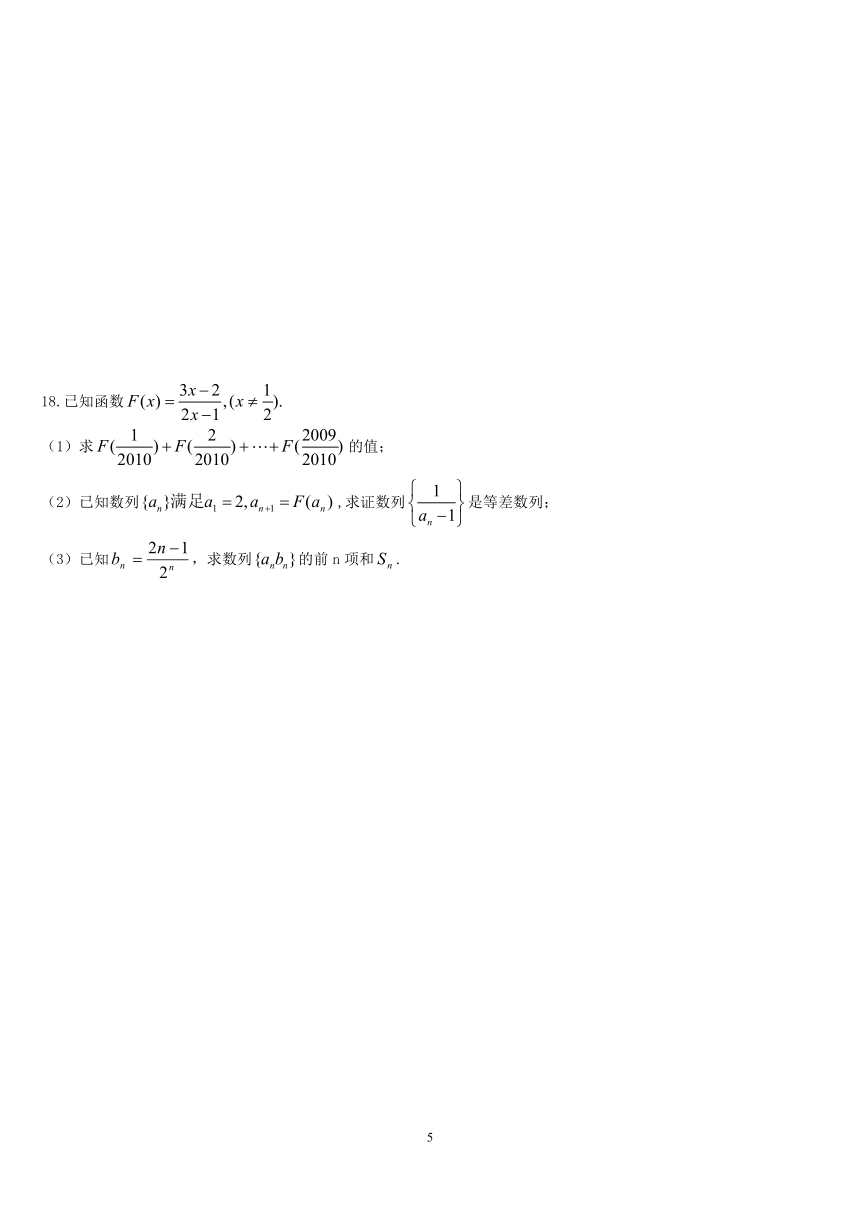
文档简介
黑龙江省绥化市第九中学2013届高三第二次月考试题数学卷(理科)
一选择题:(共12小题,每题5分,合计60分)
1.已知集合,时,( )
A. B. C. D.
2. 复数的实部是( )
A.2 B.4 C.3 D.-2
3. 等差数列的前n项和为,若为一确定常数,则下列各式也为确定常数的是( )
A. B. C. D.
4. 已知=2,=,=1,则向量与的夹角为 ( )
A. B. C. D.
5. 执行如图所示的程序框图,若输入x=3,则输出y的值为( )
A.5 B.9 C.17 D.33
6.已知函数,则( )
A. B. C. D.
7. 已知双曲线的两条渐近线均与相切,则该双曲线离心率等于( )
A. B. C. D.
8. 如图,一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形,则其体积是( )
A. B. C. D.
9.己知△ABC的外心、重心、垂心分别为O,G,H,若,则=( C )
A. B. C.3 D.2
10.下列四种说法中,错误的个数是:( )
①的子集有个;
②命题“存在”的否定是:“不存在;
③函数的切线斜率的最大值是;
④已知函数满足且,则.
A. B. C. D.
11.若方程的任意一组解()都满足不等式,则的取值范围是( )
A. B. C. D.
12.函数为定义在上的减函数,函数的图像关于点(1,0)对称, 满足不等式,,为坐标原点,则当时,的取值范围为 ( )
A. B. C. D.
班级
姓名
二填空题(共4小题,每小题5分,合计20分)
13. 以抛物线y2=4x上的点A(4.,4)为圆心,且与抛物线的准线相切的圆被x轴截得的弦长为____.
14. .
15. 若直线(,)被圆截得的弦长为4,则的最小值为
16.设定义在R上的函数有5个不同实数解,则的取值范围为:___。
三:解答题(共6道大题,17、18、19、20、21题均为12分,22题为10分,合计70分)
17.已知,且
(1)求的最小正周期及单调递增区间.
(2)在△ABC中,a,b,c,分别是A,B,C的对边,若成立 ,
求的取值范围.
18.已知函数
(1)求的值;
(2)已知数列,求证数列是等差数列;
(3)已知,求数列的前n项和.
19.如图,在底面是正方形的四棱锥中,面,交于点,是中点,为上一点.
⑴求证:;
⑵确定点在线段上的位置,使//平面,并说明理由.
⑶当二面角的大小为时,求与底面所成角的正切值.
20.已知动圆过定点,且与直线相切,椭圆的对称轴为坐标轴,一个焦点为,点在椭圆上.
(1)求动圆圆心的轨迹的方程及椭圆的方程;
(2)若动直线与轨迹在处的切线平行,且直线与椭圆交于两点,试求当面积取到最大值时直线的方程.
21. 已知函数
(Ⅰ)当时,求函数的最值;
(Ⅱ)求函数的单调区间;
(Ⅱ)试说明是否存在实数使的图象与无公共点.
22.在极坐标系中,曲线C1方程为=2sin(θ+ ),曲线C2:方程为sin(θ+ )=4.以极点O为原点,极轴方向为x轴正向建立直角坐标系xOy.
(1)求曲线C1,C2的直角坐标方程
(2)设A. B分别是C1,C2上的动点,求|AB|的最小值.
黑龙江省绥化市第九中学2013届高三10月考试题理科数学答题卡
班级
姓名
二填空题(共4小题,每小题5分,合计20分)
13. ____ 14. _____ 15. ____ 16.____
三:解答题(共6道大题,17、18、19、20、21题均为12分,22题为10分,合计70分)
17.已知,且
(1)求的最小正周期及单调递增区间.
(2)在△ABC中,a,b,c,分别是A,B,C的对边,若成立 ,
求的取值范围.
18.已知函数
(1)求的值;
(2)已知数列,求证数列是等差数列;
(3)已知,求数列的前n项和.
班级
姓名
19.如图,在底面是正方形的四棱锥中,面,交于点,是中点,为上一点.
⑴求证:;
⑵确定点在线段上的位置,使//平面,并说明理由.
⑶当二面角的大小为时,求与底面所成角的正切值.
20.已知动圆过定点,且与直线相切,椭圆的对称轴为坐标轴,一个焦点为,点在椭圆上.
(1)求动圆圆心的轨迹的方程及椭圆的方程;
(2)若动直线与轨迹在处的切线平行,且直线与椭圆交于两点,试求当面积取到最大值时直线的方程.
21. 已知函数
(Ⅰ)当时,求函数的最值;
(Ⅱ)求函数的单调区间;
(Ⅱ)试说明是否存在实数使的图象与无公共点.
22.在极坐标系中,曲线C1方程为=2sin(θ+ ),曲线C2:方程为sin(θ+ )=4.以极点O为原点,极轴方向为x轴正向建立直角坐标系xOy.
(Ⅰ)求曲线C1,C2的直角坐标方程
(Ⅱ)设A. B分别是C1,C2上的动点,求|AB|的最小值.
黑龙江省绥化市第九中学2013届高三10月考试题理科数学参考答案
一选择题:1-5BACBD;6-10AACCC;11-12DD
二填空题:13.6;14. ;15. ;16.
三解答题:
17解:(1)
单调递增区间为:
解得:
故单调递增区间为:
(2)由正弦定理得:
B为三角形的内角 B=
+1
又
故2,3]
18.解: (1)因为.
所以设S=…………(1)
S=. ………(2)
(1)+(2)得:
=, 所以S=.
(2)由两边同减去1,得.
所以,
所以,是以2为公差以为首项的等差数列.
(3)因为.
因为,所以
= (3)
= (4)
由(3)-(4)得
==
所以=
19.⑴∵面,四边形是正方形,其对角线,交于点,
∴,.
∴平面,
∵平面,
∴
⑵当为中点,即时,平面,理由如下:
连结,由为中点,为中点,知,
而平面,平面,
故平面.
⑶作于,连结,
∵面,四边形是正方形,
∴,
又∵,,∴,
∴,且,
∴是二面角的平面角,
即,
另解:以为原点,、、所在的直线分别为、、轴建立空间直角坐标系如图所示,
设正方形的边长为,则,,,,,,,.
⑴,,
∴
⑵要使平面,只需,而,
由可得,解得,,
∴,∴
故当时,平面
设平面的一个法向量为,
则,而,,
∴,取,得,
同理可得平面的一个法向量
设所成的角为,则,
即,∴,∴
∵面,∴就是与底面所成的角,
∴.
20. 解:(1)过圆心M作直线的垂线,垂足为H.
由题意得,|MH|=|MF|,由抛物线定义得,点M的轨迹是以为焦点,直线为准线的抛物线,其方程为. 设椭圆方程为,将点A代入方程整理得解得 .
故所求的椭圆方程为
(2)轨迹的方程为,即.
则,所以轨迹在处的切线斜率为,
设直线方程为,代入椭圆方程得
因为 ,解得;
设
所以
点A到直线的距离为.
所以
当且仅当,即时等号成立,此时直线的方程为
21. 解:(Ⅰ)函数的定义域是(1,+)
当a=1时,,所以在为减函数
在为增函数,所以函数的最小值为.
(Ⅱ),
若时,则>0在(1,)恒成立,
所以的增区间(1,)
若,故当,,
当时,,
所以a>0时的减区间为(),的增区间为[.
(Ⅲ)时,由(Ⅰ)知在(1,+)的最小值为,.
令在[1,+)上单调递减,
所以,则
因此存在实数使的最小值大于,
故存在实数使y=的图象与y=无公共点.
22解:(Ⅰ)曲线C1的极坐标方程化为ρ=sinθ+cosθ,
两边同乘以ρ,得ρ2=ρsinθ+ρcosθ,
则曲线C1的直角坐标方程为x2+y2=y+x,即x2+y2-x-y=0.
曲线C2的极坐标方程化为ρsinθ+ρcosθ=4,
则曲线C2的的直角坐标方程为y+x=4,即x+y-8=0.
(Ⅱ)将曲线C1的直角坐标方程化为(x-)2+(y-)2=1,
它表示以(,)为圆心,以1为半径的圆.
该圆圆心到曲线C2即直线x+y-8=0的距离
d==3,
所以|AB|的最小值为2.
第5小题
第8小题
PAGE
1
一选择题:(共12小题,每题5分,合计60分)
1.已知集合,时,( )
A. B. C. D.
2. 复数的实部是( )
A.2 B.4 C.3 D.-2
3. 等差数列的前n项和为,若为一确定常数,则下列各式也为确定常数的是( )
A. B. C. D.
4. 已知=2,=,=1,则向量与的夹角为 ( )
A. B. C. D.
5. 执行如图所示的程序框图,若输入x=3,则输出y的值为( )
A.5 B.9 C.17 D.33
6.已知函数,则( )
A. B. C. D.
7. 已知双曲线的两条渐近线均与相切,则该双曲线离心率等于( )
A. B. C. D.
8. 如图,一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形,则其体积是( )
A. B. C. D.
9.己知△ABC的外心、重心、垂心分别为O,G,H,若,则=( C )
A. B. C.3 D.2
10.下列四种说法中,错误的个数是:( )
①的子集有个;
②命题“存在”的否定是:“不存在;
③函数的切线斜率的最大值是;
④已知函数满足且,则.
A. B. C. D.
11.若方程的任意一组解()都满足不等式,则的取值范围是( )
A. B. C. D.
12.函数为定义在上的减函数,函数的图像关于点(1,0)对称, 满足不等式,,为坐标原点,则当时,的取值范围为 ( )
A. B. C. D.
班级
姓名
二填空题(共4小题,每小题5分,合计20分)
13. 以抛物线y2=4x上的点A(4.,4)为圆心,且与抛物线的准线相切的圆被x轴截得的弦长为____.
14. .
15. 若直线(,)被圆截得的弦长为4,则的最小值为
16.设定义在R上的函数有5个不同实数解,则的取值范围为:___。
三:解答题(共6道大题,17、18、19、20、21题均为12分,22题为10分,合计70分)
17.已知,且
(1)求的最小正周期及单调递增区间.
(2)在△ABC中,a,b,c,分别是A,B,C的对边,若成立 ,
求的取值范围.
18.已知函数
(1)求的值;
(2)已知数列,求证数列是等差数列;
(3)已知,求数列的前n项和.
19.如图,在底面是正方形的四棱锥中,面,交于点,是中点,为上一点.
⑴求证:;
⑵确定点在线段上的位置,使//平面,并说明理由.
⑶当二面角的大小为时,求与底面所成角的正切值.
20.已知动圆过定点,且与直线相切,椭圆的对称轴为坐标轴,一个焦点为,点在椭圆上.
(1)求动圆圆心的轨迹的方程及椭圆的方程;
(2)若动直线与轨迹在处的切线平行,且直线与椭圆交于两点,试求当面积取到最大值时直线的方程.
21. 已知函数
(Ⅰ)当时,求函数的最值;
(Ⅱ)求函数的单调区间;
(Ⅱ)试说明是否存在实数使的图象与无公共点.
22.在极坐标系中,曲线C1方程为=2sin(θ+ ),曲线C2:方程为sin(θ+ )=4.以极点O为原点,极轴方向为x轴正向建立直角坐标系xOy.
(1)求曲线C1,C2的直角坐标方程
(2)设A. B分别是C1,C2上的动点,求|AB|的最小值.
黑龙江省绥化市第九中学2013届高三10月考试题理科数学答题卡
班级
姓名
二填空题(共4小题,每小题5分,合计20分)
13. ____ 14. _____ 15. ____ 16.____
三:解答题(共6道大题,17、18、19、20、21题均为12分,22题为10分,合计70分)
17.已知,且
(1)求的最小正周期及单调递增区间.
(2)在△ABC中,a,b,c,分别是A,B,C的对边,若成立 ,
求的取值范围.
18.已知函数
(1)求的值;
(2)已知数列,求证数列是等差数列;
(3)已知,求数列的前n项和.
班级
姓名
19.如图,在底面是正方形的四棱锥中,面,交于点,是中点,为上一点.
⑴求证:;
⑵确定点在线段上的位置,使//平面,并说明理由.
⑶当二面角的大小为时,求与底面所成角的正切值.
20.已知动圆过定点,且与直线相切,椭圆的对称轴为坐标轴,一个焦点为,点在椭圆上.
(1)求动圆圆心的轨迹的方程及椭圆的方程;
(2)若动直线与轨迹在处的切线平行,且直线与椭圆交于两点,试求当面积取到最大值时直线的方程.
21. 已知函数
(Ⅰ)当时,求函数的最值;
(Ⅱ)求函数的单调区间;
(Ⅱ)试说明是否存在实数使的图象与无公共点.
22.在极坐标系中,曲线C1方程为=2sin(θ+ ),曲线C2:方程为sin(θ+ )=4.以极点O为原点,极轴方向为x轴正向建立直角坐标系xOy.
(Ⅰ)求曲线C1,C2的直角坐标方程
(Ⅱ)设A. B分别是C1,C2上的动点,求|AB|的最小值.
黑龙江省绥化市第九中学2013届高三10月考试题理科数学参考答案
一选择题:1-5BACBD;6-10AACCC;11-12DD
二填空题:13.6;14. ;15. ;16.
三解答题:
17解:(1)
单调递增区间为:
解得:
故单调递增区间为:
(2)由正弦定理得:
B为三角形的内角 B=
+1
又
故2,3]
18.解: (1)因为.
所以设S=…………(1)
S=. ………(2)
(1)+(2)得:
=, 所以S=.
(2)由两边同减去1,得.
所以,
所以,是以2为公差以为首项的等差数列.
(3)因为.
因为,所以
= (3)
= (4)
由(3)-(4)得
==
所以=
19.⑴∵面,四边形是正方形,其对角线,交于点,
∴,.
∴平面,
∵平面,
∴
⑵当为中点,即时,平面,理由如下:
连结,由为中点,为中点,知,
而平面,平面,
故平面.
⑶作于,连结,
∵面,四边形是正方形,
∴,
又∵,,∴,
∴,且,
∴是二面角的平面角,
即,
另解:以为原点,、、所在的直线分别为、、轴建立空间直角坐标系如图所示,
设正方形的边长为,则,,,,,,,.
⑴,,
∴
⑵要使平面,只需,而,
由可得,解得,,
∴,∴
故当时,平面
设平面的一个法向量为,
则,而,,
∴,取,得,
同理可得平面的一个法向量
设所成的角为,则,
即,∴,∴
∵面,∴就是与底面所成的角,
∴.
20. 解:(1)过圆心M作直线的垂线,垂足为H.
由题意得,|MH|=|MF|,由抛物线定义得,点M的轨迹是以为焦点,直线为准线的抛物线,其方程为. 设椭圆方程为,将点A代入方程整理得解得 .
故所求的椭圆方程为
(2)轨迹的方程为,即.
则,所以轨迹在处的切线斜率为,
设直线方程为,代入椭圆方程得
因为 ,解得;
设
所以
点A到直线的距离为.
所以
当且仅当,即时等号成立,此时直线的方程为
21. 解:(Ⅰ)函数的定义域是(1,+)
当a=1时,,所以在为减函数
在为增函数,所以函数的最小值为.
(Ⅱ),
若时,则>0在(1,)恒成立,
所以的增区间(1,)
若,故当,,
当时,,
所以a>0时的减区间为(),的增区间为[.
(Ⅲ)时,由(Ⅰ)知在(1,+)的最小值为,.
令在[1,+)上单调递减,
所以,则
因此存在实数使的最小值大于,
故存在实数使y=的图象与y=无公共点.
22解:(Ⅰ)曲线C1的极坐标方程化为ρ=sinθ+cosθ,
两边同乘以ρ,得ρ2=ρsinθ+ρcosθ,
则曲线C1的直角坐标方程为x2+y2=y+x,即x2+y2-x-y=0.
曲线C2的极坐标方程化为ρsinθ+ρcosθ=4,
则曲线C2的的直角坐标方程为y+x=4,即x+y-8=0.
(Ⅱ)将曲线C1的直角坐标方程化为(x-)2+(y-)2=1,
它表示以(,)为圆心,以1为半径的圆.
该圆圆心到曲线C2即直线x+y-8=0的距离
d==3,
所以|AB|的最小值为2.
第5小题
第8小题
PAGE
1
同课章节目录
