安徽省淮北一中2012-2013学年高二上学期第一次月考数学试题
文档属性
| 名称 | 安徽省淮北一中2012-2013学年高二上学期第一次月考数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 152.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-22 00:00:00 | ||
图片预览



文档简介
淮北一中2012-2013学年高二第一次月考数学试题
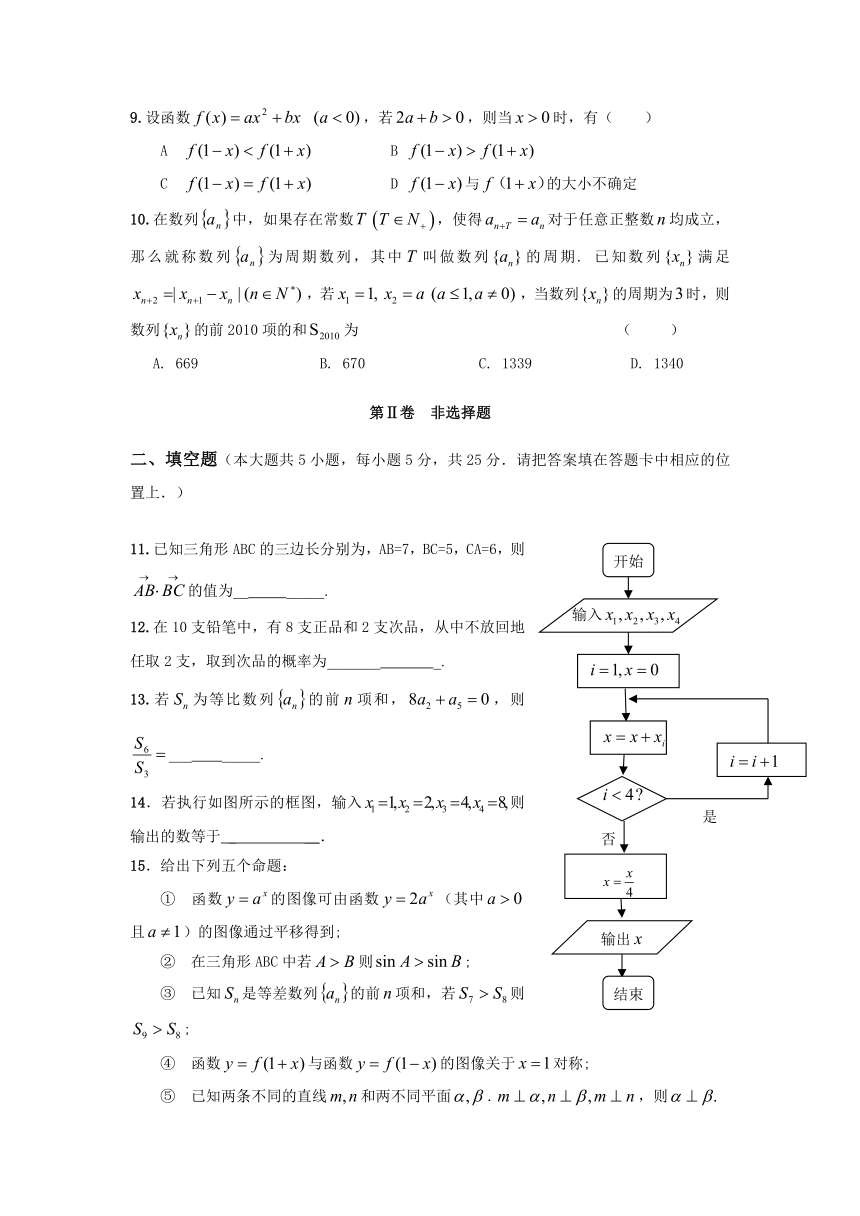
第I卷 选择题
一.选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.集合,集合,则( )
某中学高一年级有540人,高二年级有440人,高三年级有420人。用分层抽样的方法抽取样本容量为70的样本,则,高一、高二、高三,三个年级分别抽取( )
A.28人,24人,18人 B 25人,24人,21人
C 26人,24人,20人 D 27人,22人,21人
3.数列,前n项和为( )
4.已知直线与圆相切,则三条边长分别为的三角形( )
A.是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
5.在中,,则的值为( )
6.有一个几何体的正视、侧视、俯视图分别如下,则该几何体的表面积为( )
正视图 侧视图 俯视图
A B C D
7.等比数列中,已知,则此数列前17项之积为( )
A. B.- C. D.-
8.将函数的图象上每点的横坐标缩小为原来的(纵坐标不变),再把所得图象向左平移个单位,得到的函数解析式为( )
9.设函数 ,若,则当时,有( )
A B
C D 与的大小不确定
在数列中,如果存在常数,使得对于任意正整数均成立,那么就称数列为周期数列,其中叫做数列的周期. 已知数列满足,若,当数列的周期为时,则数列的前2010项的和为 ( )
A. 669 B. 670 C. 1339 D. 1340
第Ⅱ卷 非选择题
二、填空题(本大题共5小题,每小题5分,共25分.请把答案填在答题卡中相应的位置上.)
11.已知三角形ABC的三边长分别为,AB=7,BC=5,CA=6,则的值为__ _____.
12.在10支铅笔中,有8支正品和2支次品,从中不放回地任取2支,取到次品的概率为_______ _.
13.若为等比数列的前项和,,则___ _____.
14.若执行如图所示的框图,输入则 输出的数等于 _ __.
15.给出下列五个命题:
① 函数的图像可由函数(其中且)的图像通过平移得到;
② 在三角形ABC中若则;
③ 已知是等差数列的前项和,若则;
④ 函数与函数的图像关于对称;
⑤ 已知两条不同的直线和两不同平面.,则
其中正确命题的序号为: _ __.
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.只写答案不得分。)
16.(本小题满分12分)在三角形ABC中,角A、B、C所对的边分别为a、b、c。角A、B、C成等差数列,边a、b、c成等比数列。
(1)求角B的大小。
(2)判断三角形ABC的形状。
17.(本小题满分12)已知在递增数列中,,。
(1)若是等差数列,求的通项公式。
(2)若是等比数列,求的通项公式。
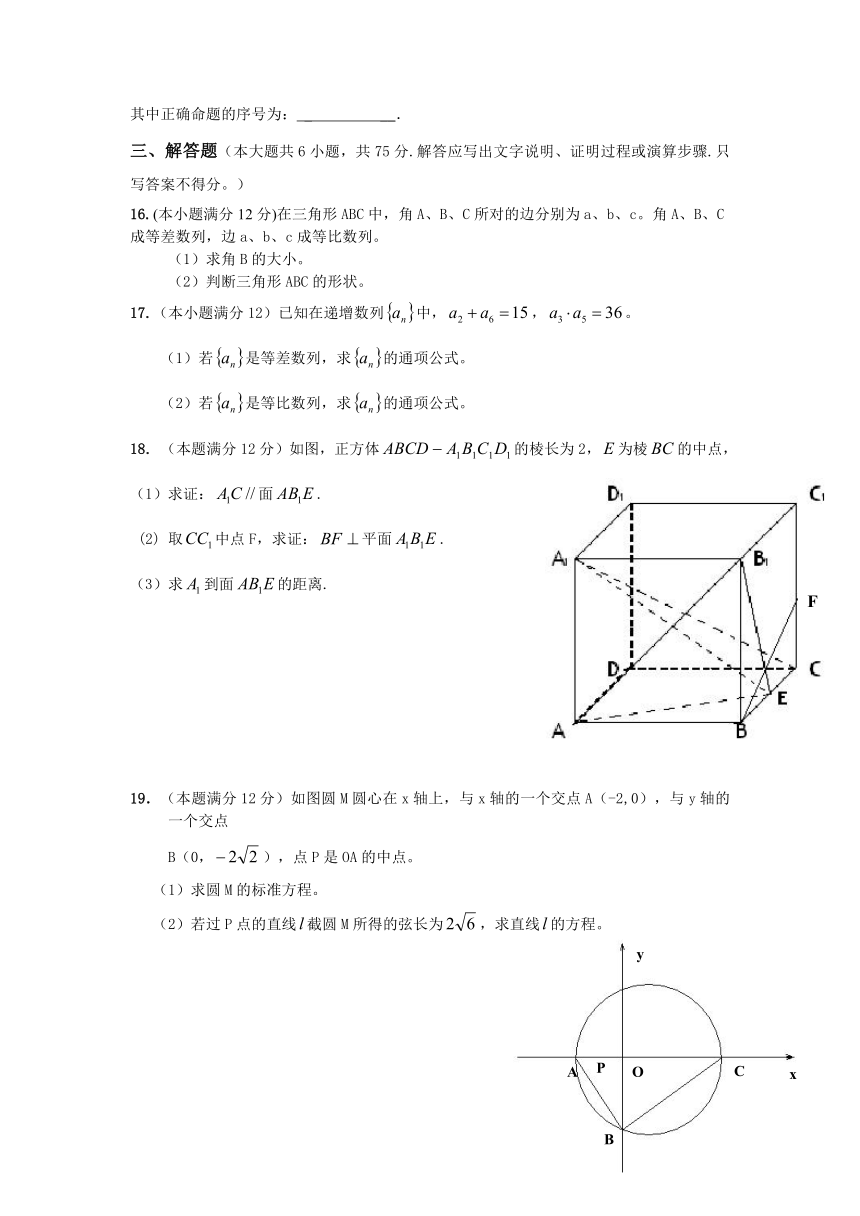
18. (本题满分12分)如图,正方体的棱长为2,为棱的中点,
(1)求证:面.
(2) 取中点F,求证:平面.
(3)求到面的距离.
(本题满分12分)如图圆M圆心在x轴上,与x轴的一个交点A(-2,0),与y轴的一个交点
B(0,),点P是OA的中点。
(1)求圆M的标准方程。
(2)若过P点的直线截圆M所得的弦长为,求直线的方程。
(本题满分13分)
已知△ABC的内角A、B、C所对的边分别为.向量,。
(1)求角B的大小。
(2)若,求边的值。
21. (本题满分14分)
(理)已知数列中,是其前项和,并且,
⑴ 设数列,求证:数列是等比数列;
⑵ 设数列,求证:数列是等差数列;
⑶ 求数列的通项公式及前项和。
(文)设正值数列{}的前n项和为,满足
(1)求,,
(2)求出数列{}的通项公式(写出推导过程)
(3)设 求数列{}的前n项和
淮北一中2012-2013学年高二第一次月考数学试题
(参考答案)
选择题
1、B 2、D 3、A 4、B 5、A 6、B 7、D 8、B 9、A 10D
填空题
11、-19. 12、 13、-7 14、 15.①②⑤
简答题(解答应写出文字说明、证明过程或演算步骤.只写答案不得分。)
16、解:(1)由题可知:角A、B、C成等差数列,故可设A=B﹣d,C=B+d
则A+B+C=(B﹣d)+B+(B+d)=,
故B=………………………………………………………………………………6
(2)法一、角的关系转化为边的关系。
边a、b、c成等比数列,则 ①
由(1)可知:B=,结合余弦定理得:
=。
则有
结合①式得即
所以,
又B=。
所以三角形ABC为正三角形。
法二、边的关系转化为角的关系。
边a、b、c成等比数列,则
结合正弦定理可知:
由(1)可知:B=
则有
又B+C=,所以
即
故
可得:,由辅助角公式可得:。
又,故。
结合可得:,即。
又B=。
所以三角形ABC为正三角形。………………………………………………………12
17、解:(1)由题可知:若是等差数列
则有:。又。
故有:或。
又数列是递增数列,故
则等差数列的首项,公差。
故等差数列的通项公式为:………………………………6
(2)由题可知:若是等比数列
则有:,又。
故有:或。
又数列是递增数列
故且数列的首项,公比。
所以等比数列的通项公式为:……………………………12
18、解:(1)证明:连接,交于点,则为的中点,连接,由于是的中点,故是三角形。底边的中位线。故∥,又面,面,故∥面。……………………………………4
(2)证明:由是正方体,可知:面.又面。故。
又,在正方形中,因为,,。所以≌。则,。故,故。
而,,故…………………8
(3)由正方体棱长为2可得:,.结合余弦定理可得:=.则。可得=。
又.。
设到的距离为。则有,
即。故。…………12
解:(1)由题可知:ABC是直角三角形,角B为直角。又OBAC。故.则,,圆M半径为3,M点的坐标为(1,0).
圆M标准方程为:……………………………………5
(2)由点P是OA的中点知P点坐标为(-1,0)。
当设过P点的直线斜率不存在时,方程为,此时截得的弦长为,不满足题意,故斜率存在。……………………………………………………………7
设过P点的直线方程为,由于圆M半径为3故要使得截得的弦长为只需要圆心M到直线距离为,即,解得。即直线的方程为……………………12
解:(1)由可知
即,
则有,,故角B的大小为或。…………………6
(2)解法一:由余弦定理求解
若,,则,故角B的大小为。结合余弦定理可得:
,即,又,可知:,可得或。
解法二:由正弦定理求解
由正弦定理可得,,所以,故,
,或,
若,,,故。
若则
综上可知:或。………………………………………………………13
(理科)解:(1)由数列其前项和满足:,①
可知当时,有:,②.
①-②得,,故有,
又当时,又可得,故,可知数列是以为首项,公比为2的等比数列。………4
(2)由(1)可知:当时
可得即,
数列是以为首项公差为等差数列。……………………………8
(3)由(2)可知:故,
当时,
当时,=。
又当时合适,……………………………………………………………12
故数列的及前项和=。…………………………………14
(文科)(1)当时故。
当时又,故。
当时又,,故。………4
(2)由数列其前项和满足:,可得:,①
当时故。
当时, ②
①-②得:,即由于是正值数列,故,可得,所以是以为首项,公差为2的等差数列。则。
又当时合适通式
故数列{}的通项公式为……………………………………9
(3)由(2)可知:=。
故数列{}的前n项和
=……………………………14
6
5
6
5
开始
输入
开始
开始
否
是
结束
输出
开始
F
y
P
O
A
B
C
x
第I卷 选择题
一.选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.集合,集合,则( )
某中学高一年级有540人,高二年级有440人,高三年级有420人。用分层抽样的方法抽取样本容量为70的样本,则,高一、高二、高三,三个年级分别抽取( )
A.28人,24人,18人 B 25人,24人,21人
C 26人,24人,20人 D 27人,22人,21人
3.数列,前n项和为( )
4.已知直线与圆相切,则三条边长分别为的三角形( )
A.是锐角三角形 B.是直角三角形 C.是钝角三角形 D.不存在
5.在中,,则的值为( )
6.有一个几何体的正视、侧视、俯视图分别如下,则该几何体的表面积为( )
正视图 侧视图 俯视图
A B C D
7.等比数列中,已知,则此数列前17项之积为( )
A. B.- C. D.-
8.将函数的图象上每点的横坐标缩小为原来的(纵坐标不变),再把所得图象向左平移个单位,得到的函数解析式为( )
9.设函数 ,若,则当时,有( )
A B
C D 与的大小不确定
在数列中,如果存在常数,使得对于任意正整数均成立,那么就称数列为周期数列,其中叫做数列的周期. 已知数列满足,若,当数列的周期为时,则数列的前2010项的和为 ( )
A. 669 B. 670 C. 1339 D. 1340
第Ⅱ卷 非选择题
二、填空题(本大题共5小题,每小题5分,共25分.请把答案填在答题卡中相应的位置上.)
11.已知三角形ABC的三边长分别为,AB=7,BC=5,CA=6,则的值为__ _____.
12.在10支铅笔中,有8支正品和2支次品,从中不放回地任取2支,取到次品的概率为_______ _.
13.若为等比数列的前项和,,则___ _____.
14.若执行如图所示的框图,输入则 输出的数等于 _ __.
15.给出下列五个命题:
① 函数的图像可由函数(其中且)的图像通过平移得到;
② 在三角形ABC中若则;
③ 已知是等差数列的前项和,若则;
④ 函数与函数的图像关于对称;
⑤ 已知两条不同的直线和两不同平面.,则
其中正确命题的序号为: _ __.
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.只写答案不得分。)
16.(本小题满分12分)在三角形ABC中,角A、B、C所对的边分别为a、b、c。角A、B、C成等差数列,边a、b、c成等比数列。
(1)求角B的大小。
(2)判断三角形ABC的形状。
17.(本小题满分12)已知在递增数列中,,。
(1)若是等差数列,求的通项公式。
(2)若是等比数列,求的通项公式。
18. (本题满分12分)如图,正方体的棱长为2,为棱的中点,
(1)求证:面.
(2) 取中点F,求证:平面.
(3)求到面的距离.
(本题满分12分)如图圆M圆心在x轴上,与x轴的一个交点A(-2,0),与y轴的一个交点
B(0,),点P是OA的中点。
(1)求圆M的标准方程。
(2)若过P点的直线截圆M所得的弦长为,求直线的方程。
(本题满分13分)
已知△ABC的内角A、B、C所对的边分别为.向量,。
(1)求角B的大小。
(2)若,求边的值。
21. (本题满分14分)
(理)已知数列中,是其前项和,并且,
⑴ 设数列,求证:数列是等比数列;
⑵ 设数列,求证:数列是等差数列;
⑶ 求数列的通项公式及前项和。
(文)设正值数列{}的前n项和为,满足
(1)求,,
(2)求出数列{}的通项公式(写出推导过程)
(3)设 求数列{}的前n项和
淮北一中2012-2013学年高二第一次月考数学试题
(参考答案)
选择题
1、B 2、D 3、A 4、B 5、A 6、B 7、D 8、B 9、A 10D
填空题
11、-19. 12、 13、-7 14、 15.①②⑤
简答题(解答应写出文字说明、证明过程或演算步骤.只写答案不得分。)
16、解:(1)由题可知:角A、B、C成等差数列,故可设A=B﹣d,C=B+d
则A+B+C=(B﹣d)+B+(B+d)=,
故B=………………………………………………………………………………6
(2)法一、角的关系转化为边的关系。
边a、b、c成等比数列,则 ①
由(1)可知:B=,结合余弦定理得:
=。
则有
结合①式得即
所以,
又B=。
所以三角形ABC为正三角形。
法二、边的关系转化为角的关系。
边a、b、c成等比数列,则
结合正弦定理可知:
由(1)可知:B=
则有
又B+C=,所以
即
故
可得:,由辅助角公式可得:。
又,故。
结合可得:,即。
又B=。
所以三角形ABC为正三角形。………………………………………………………12
17、解:(1)由题可知:若是等差数列
则有:。又。
故有:或。
又数列是递增数列,故
则等差数列的首项,公差。
故等差数列的通项公式为:………………………………6
(2)由题可知:若是等比数列
则有:,又。
故有:或。
又数列是递增数列
故且数列的首项,公比。
所以等比数列的通项公式为:……………………………12
18、解:(1)证明:连接,交于点,则为的中点,连接,由于是的中点,故是三角形。底边的中位线。故∥,又面,面,故∥面。……………………………………4
(2)证明:由是正方体,可知:面.又面。故。
又,在正方形中,因为,,。所以≌。则,。故,故。
而,,故…………………8
(3)由正方体棱长为2可得:,.结合余弦定理可得:=.则。可得=。
又.。
设到的距离为。则有,
即。故。…………12
解:(1)由题可知:ABC是直角三角形,角B为直角。又OBAC。故.则,,圆M半径为3,M点的坐标为(1,0).
圆M标准方程为:……………………………………5
(2)由点P是OA的中点知P点坐标为(-1,0)。
当设过P点的直线斜率不存在时,方程为,此时截得的弦长为,不满足题意,故斜率存在。……………………………………………………………7
设过P点的直线方程为,由于圆M半径为3故要使得截得的弦长为只需要圆心M到直线距离为,即,解得。即直线的方程为……………………12
解:(1)由可知
即,
则有,,故角B的大小为或。…………………6
(2)解法一:由余弦定理求解
若,,则,故角B的大小为。结合余弦定理可得:
,即,又,可知:,可得或。
解法二:由正弦定理求解
由正弦定理可得,,所以,故,
,或,
若,,,故。
若则
综上可知:或。………………………………………………………13
(理科)解:(1)由数列其前项和满足:,①
可知当时,有:,②.
①-②得,,故有,
又当时,又可得,故,可知数列是以为首项,公比为2的等比数列。………4
(2)由(1)可知:当时
可得即,
数列是以为首项公差为等差数列。……………………………8
(3)由(2)可知:故,
当时,
当时,=。
又当时合适,……………………………………………………………12
故数列的及前项和=。…………………………………14
(文科)(1)当时故。
当时又,故。
当时又,,故。………4
(2)由数列其前项和满足:,可得:,①
当时故。
当时, ②
①-②得:,即由于是正值数列,故,可得,所以是以为首项,公差为2的等差数列。则。
又当时合适通式
故数列{}的通项公式为……………………………………9
(3)由(2)可知:=。
故数列{}的前n项和
=……………………………14
6
5
6
5
开始
输入
开始
开始
否
是
结束
输出
开始
F
y
P
O
A
B
C
x
同课章节目录
