鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例-第二课时(课件)(共14张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 3.3 勾股定理的应用举例-第二课时(课件)(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 180.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第二课时
勾股定理的应用举例
Contents
目录
01
02
03
04
巩固练习
课堂小结
例题探究
问题情境
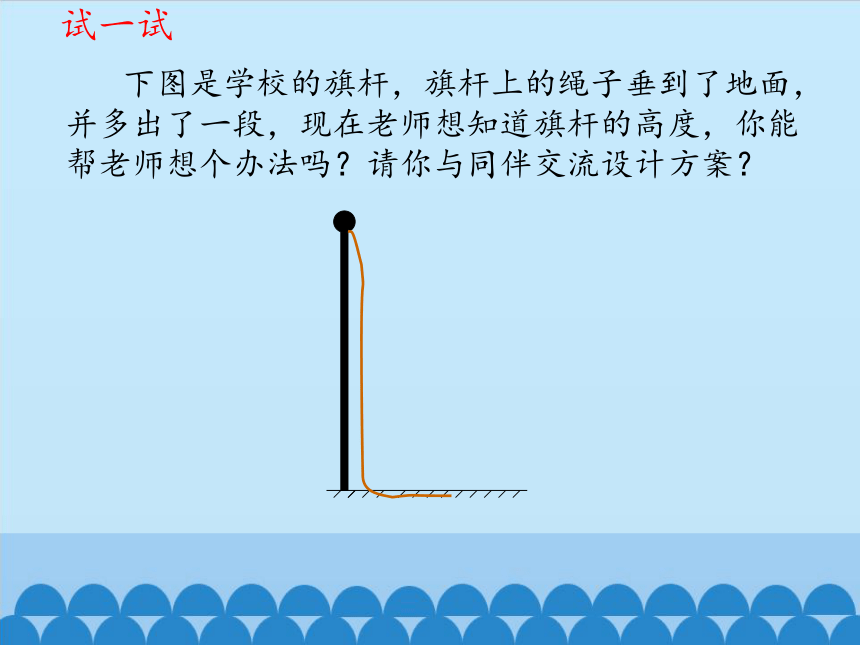
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?
试一试
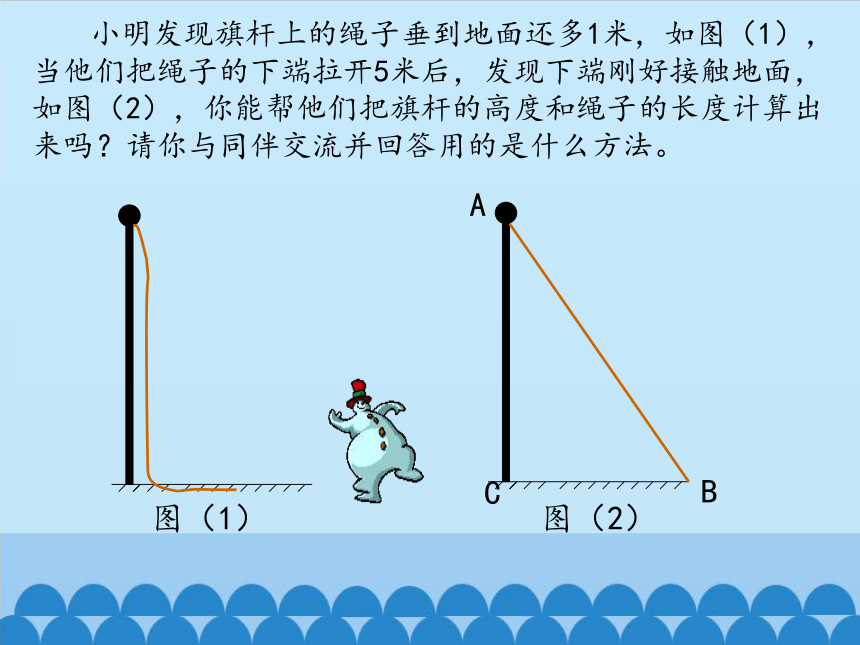
图(1)
图(2)
A
B
C
小明发现旗杆上的绳子垂到地面还多1米,如图(1),当他们把绳子的下端拉开5米后,发现下端刚好接触地面,如图(2),你能帮他们把旗杆的高度和绳子的长度计算出来吗?请你与同伴交流并回答用的是什么方法。
例1在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得,BC2+AC2=AB2
即52+x2=(x+1)2
25+x2=x2+2x+1,
2x=24,
∴x=12,x+1=13
答:水池的水深12尺,这根芦苇长13尺。
D
A
B
C
例2.如图,某隧道的截面是一个半径为4.2m的半圆形,一辆高3.6m,宽3m的卡车能通过该隧道吗?
解:隧道的横截面如图,AB的中点O是隧道的截面半圆的圆心。OB=1.5m,BC=3.6m,∠ABC为直角。
在直角三角形OBC中,由勾股定理得
隧道的截面半径r=4.2m,4.2×4.2=17.64>15.21
故卡车可以沿着该隧道中间顺利通过。
1.今早7:00,我从家出发,以100米/分的速度向西走5分钟,又以120米/分的速度向南走10分钟,到达学校。
(1)早上老师共走了多少路程?
学校
家
路口
500m
1200m
500+1200=1700(米)
北
A
C
B
北
500
1200
(2)家到学校的距离是多少?
解:由勾股定理得:
AC2=AB2+BC2
=5002+12002
=1690000
因为AC>0,所以AC=1300米。
2.如图,一座城墙高11.7m,墙外有一个宽为9m的护城河,那么一个长为15m的云梯能否到达墙的顶端?
1.根据题意正确画出图形,(曲面最短路线问题画侧面展开图)。
2.弄清题中直角三角形及线段关系。
3.根据勾股定理求未知量,或恰当设未知量,建立方程来求解。
利用勾股定理解决实际问题的一般步骤:
课后作业
1.课本随堂练习
2.课本习题3.5 1、3
谢 谢
第二课时
勾股定理的应用举例
Contents
目录
01
02
03
04
巩固练习
课堂小结
例题探究
问题情境
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?
试一试
图(1)
图(2)
A
B
C
小明发现旗杆上的绳子垂到地面还多1米,如图(1),当他们把绳子的下端拉开5米后,发现下端刚好接触地面,如图(2),你能帮他们把旗杆的高度和绳子的长度计算出来吗?请你与同伴交流并回答用的是什么方法。
例1在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
解:设水池的水深AC为x尺,则这根芦苇长AD=AB=(x+1)尺,
在直角三角形ABC中,BC=5尺
由勾股定理得,BC2+AC2=AB2
即52+x2=(x+1)2
25+x2=x2+2x+1,
2x=24,
∴x=12,x+1=13
答:水池的水深12尺,这根芦苇长13尺。
D
A
B
C
例2.如图,某隧道的截面是一个半径为4.2m的半圆形,一辆高3.6m,宽3m的卡车能通过该隧道吗?
解:隧道的横截面如图,AB的中点O是隧道的截面半圆的圆心。OB=1.5m,BC=3.6m,∠ABC为直角。
在直角三角形OBC中,由勾股定理得
隧道的截面半径r=4.2m,4.2×4.2=17.64>15.21
故卡车可以沿着该隧道中间顺利通过。
1.今早7:00,我从家出发,以100米/分的速度向西走5分钟,又以120米/分的速度向南走10分钟,到达学校。
(1)早上老师共走了多少路程?
学校
家
路口
500m
1200m
500+1200=1700(米)
北
A
C
B
北
500
1200
(2)家到学校的距离是多少?
解:由勾股定理得:
AC2=AB2+BC2
=5002+12002
=1690000
因为AC>0,所以AC=1300米。
2.如图,一座城墙高11.7m,墙外有一个宽为9m的护城河,那么一个长为15m的云梯能否到达墙的顶端?
1.根据题意正确画出图形,(曲面最短路线问题画侧面展开图)。
2.弄清题中直角三角形及线段关系。
3.根据勾股定理求未知量,或恰当设未知量,建立方程来求解。
利用勾股定理解决实际问题的一般步骤:
课后作业
1.课本随堂练习
2.课本习题3.5 1、3
谢 谢
