苏科版七年级上册2.2有理数与无理数 课件(共20张PPT)
文档属性
| 名称 | 苏科版七年级上册2.2有理数与无理数 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:00:57 | ||
图片预览







文档简介
(共20张PPT)
苏科版 七年级上册
2.2有理数与无理数
1.整数有正整数、0、负整数
如1,2,3,0,-1,-2,-3等
分数有正分数、负分数,
(m、n是整数且 )
2.整数也可以表示成分数的形式:
分数的形式为
自主学习
我们把能够写成分数形式
(m、n是整数且
)的数叫
有理数
小学里我们还学过有限小数和循环小数,它们是有理数吗?
有限小数可以化成 的形式,是有理数。
=0.333..., =0.26666..., 这些是什么小数?循环小数,反之循环小数也能化为分数的形式,它们也是有理数!
合作探究
循环小数如何化为分数可以一起学习书P17、读一读
整数和分数都是有理数
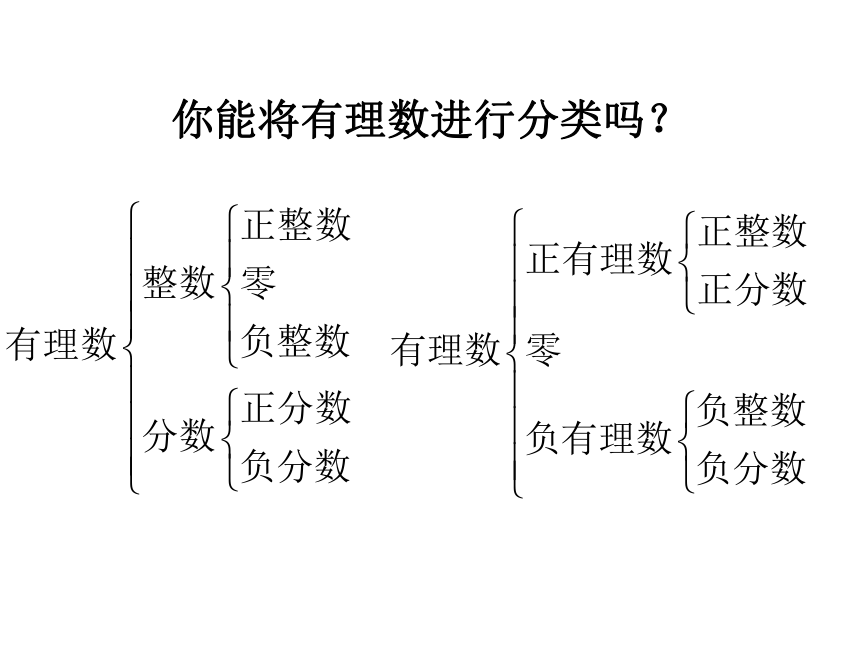
你能将有理数进行分类吗?
是不是所有的数都是有理数呢?
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
如果大正方形的边长为a,那么a2=2.a是多少?
议一议
(1)a可能是整数吗?
(2)a可能是分数吗?
(3)边长a的整数部分是几 十分位是几 百分位呢 千分位呢 ......借助计算器进行探索
边长 a 面积a2 =2
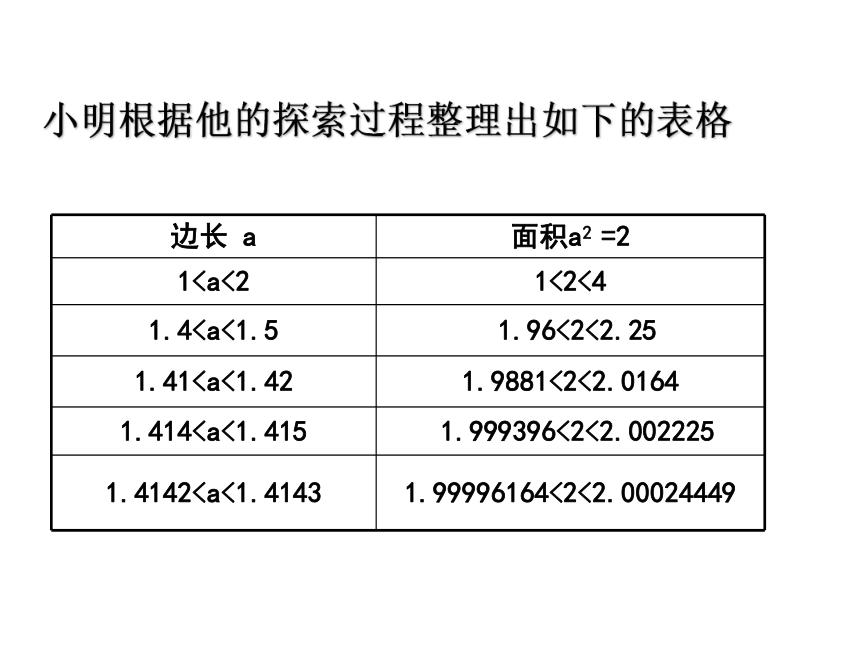
11.41.411.4141.4142小明根据他的探索过程整理出如下的表格
可能是有限小数吗?
还可以继续计算下去么?
结论:
a=1.41421356……,它是一个无限不循环小数
定义
有理数总可以用有限小数或无限循环小数表示。
反之,任何有限小数或无限循环小数也都是有理数。
无限不循环小数是无理数,反之,无理数就是无限不循环小数。
更多无理数
a=1.41421356…
b=2.2360679…
π=3.14159265…
0.58588588858888…(相邻两个5之间8的个数逐次加1)
例1 下列各数中,哪些是有理数 哪些是无理数
3.14 , π 0.57, 0.101000100 0001…(相邻两个1之间0的个数逐次加2)
解:有理数有: 3.14 , 0.57
无理数有:π, 0.101000100 0001…
交流展示
1.下列说法中,错误的是( )
A、有限小数都是有理数
B 、有理数都是有限小数
C、正数包括正有理数和正无理数,
D、负数包括负有理数和负无理数
2.以下各正方形的边长是无理数的是( )
A、面积为25的正方形 B 、面积为16的正方形
C、面积为3的正方形 D 、面积为1.44的正方形
检测反馈
3.请写出一个大于1且小于2的无理数:_______.
4.在-1.313313331,-,0,π,4中,无理数有_________个.
5.把下列各数填在相应的大括号内:
, 0, 3.14, -0.55, 8, π
1.121 221 222 1…(相邻两个1之间依次多一个2),0.2111,999.
整数集合: { }
分数集合: { }
非负整数集合:{ }
有理数集合: { }
无理数集合: { }
能力提升
如图1,纸上有五个边长为1的小正方形组成的图性纸,我们可以把它剪开拼成一个正方形如图2所示
(1)图2中拼成的正方形的边长是 ;(填“有理数”或“无理数”)
谈谈这节课收获?还有什么疑问?
小结
必做P17 习题 2.2 第1、2、题
布置作业
谢 谢!
苏科版 七年级上册
2.2有理数与无理数
1.整数有正整数、0、负整数
如1,2,3,0,-1,-2,-3等
分数有正分数、负分数,
(m、n是整数且 )
2.整数也可以表示成分数的形式:
分数的形式为
自主学习
我们把能够写成分数形式
(m、n是整数且
)的数叫
有理数
小学里我们还学过有限小数和循环小数,它们是有理数吗?
有限小数可以化成 的形式,是有理数。
=0.333..., =0.26666..., 这些是什么小数?循环小数,反之循环小数也能化为分数的形式,它们也是有理数!
合作探究
循环小数如何化为分数可以一起学习书P17、读一读
整数和分数都是有理数
你能将有理数进行分类吗?
是不是所有的数都是有理数呢?
将两个边长为1的小正方形,沿图中红线剪开,重新拼成一个大正方形,它的面积为2.
如果大正方形的边长为a,那么a2=2.a是多少?
议一议
(1)a可能是整数吗?
(2)a可能是分数吗?
(3)边长a的整数部分是几 十分位是几 百分位呢 千分位呢 ......借助计算器进行探索
边长 a 面积a2 =2
1
可能是有限小数吗?
还可以继续计算下去么?
结论:
a=1.41421356……,它是一个无限不循环小数
定义
有理数总可以用有限小数或无限循环小数表示。
反之,任何有限小数或无限循环小数也都是有理数。
无限不循环小数是无理数,反之,无理数就是无限不循环小数。
更多无理数
a=1.41421356…
b=2.2360679…
π=3.14159265…
0.58588588858888…(相邻两个5之间8的个数逐次加1)
例1 下列各数中,哪些是有理数 哪些是无理数
3.14 , π 0.57, 0.101000100 0001…(相邻两个1之间0的个数逐次加2)
解:有理数有: 3.14 , 0.57
无理数有:π, 0.101000100 0001…
交流展示
1.下列说法中,错误的是( )
A、有限小数都是有理数
B 、有理数都是有限小数
C、正数包括正有理数和正无理数,
D、负数包括负有理数和负无理数
2.以下各正方形的边长是无理数的是( )
A、面积为25的正方形 B 、面积为16的正方形
C、面积为3的正方形 D 、面积为1.44的正方形
检测反馈
3.请写出一个大于1且小于2的无理数:_______.
4.在-1.313313331,-,0,π,4中,无理数有_________个.
5.把下列各数填在相应的大括号内:
, 0, 3.14, -0.55, 8, π
1.121 221 222 1…(相邻两个1之间依次多一个2),0.2111,999.
整数集合: { }
分数集合: { }
非负整数集合:{ }
有理数集合: { }
无理数集合: { }
能力提升
如图1,纸上有五个边长为1的小正方形组成的图性纸,我们可以把它剪开拼成一个正方形如图2所示
(1)图2中拼成的正方形的边长是 ;(填“有理数”或“无理数”)
谈谈这节课收获?还有什么疑问?
小结
必做P17 习题 2.2 第1、2、题
布置作业
谢 谢!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
