2021-2022学年人教版数学九年级上册24.2.2切线的判定与性质 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.2.2切线的判定与性质 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 590.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:19:32 | ||
图片预览


文档简介
(共20张PPT)
人教版九年级数学上册
24.2 切线的判定与性质
第24章 圆
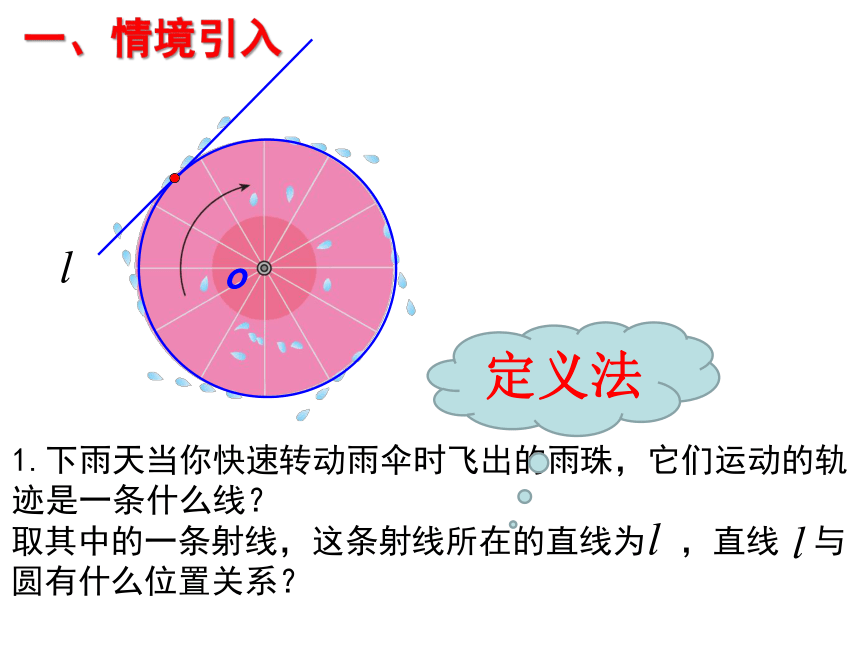
1.下雨天当你快速转动雨伞时飞出的雨珠,它们运动的轨迹是一条什么线?
一、情境引入
o
取其中的一条射线,这条射线所在的直线为 ,直线 与
圆有什么位置关系?
定义法
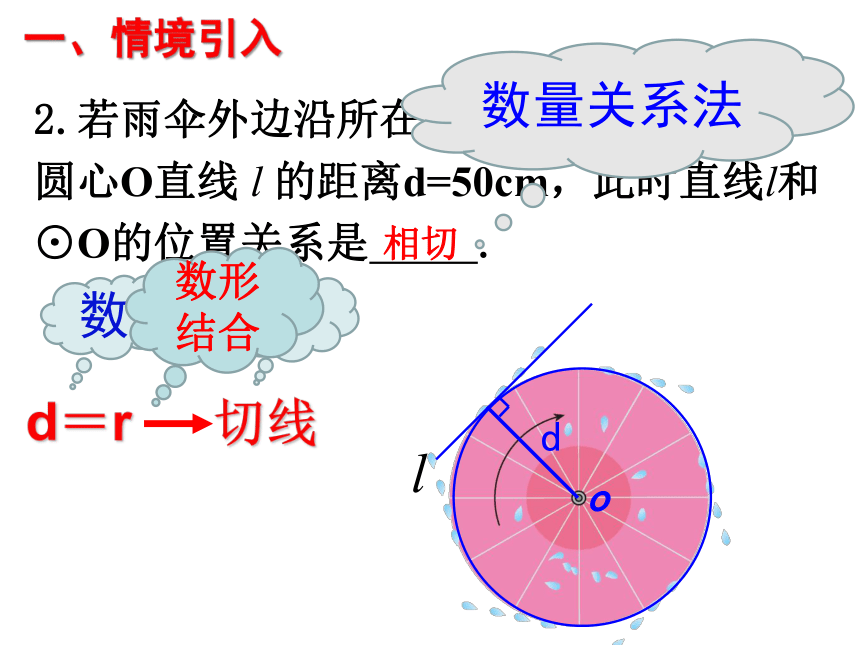
2.若雨伞外边沿所在圆的半径r为50cm,
圆心O直线 l 的距离d=50cm,此时直线l和
⊙O的位置关系是 .
相切
d=r
切线
一、情境引入
o
d
数
形
数量关系法
数形结合
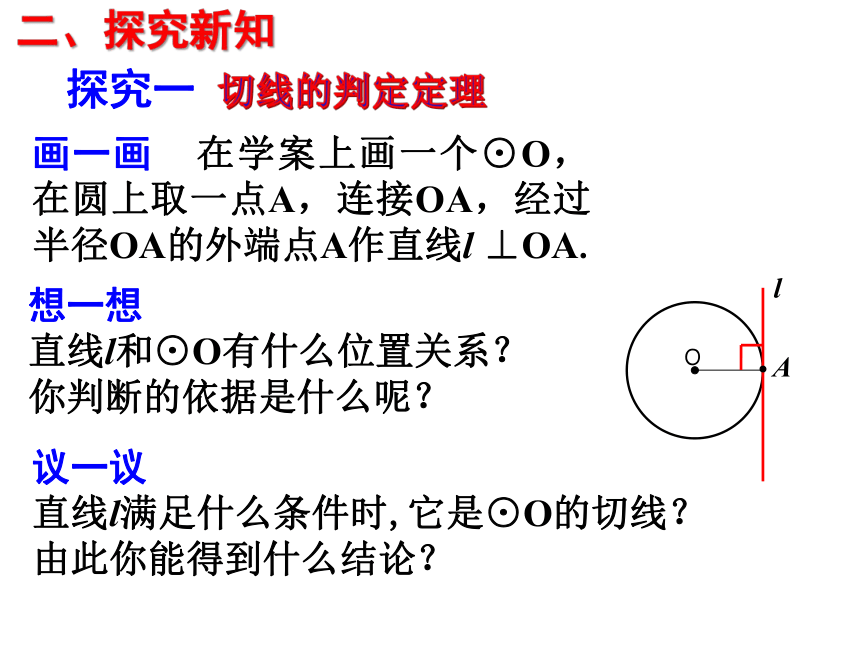
探究一 切线的判定定理
想一想
直线l和⊙O有什么位置关系?
你判断的依据是什么呢?
画一画 在学案上画一个⊙O,在圆上取一点A,连接OA,经过半径OA的外端点A作直线l ⊥OA.
O
A
l
议一议
直线l满足什么条件时,它是⊙O的切线? 由此你能得到什么结论?
.
二、探究新知
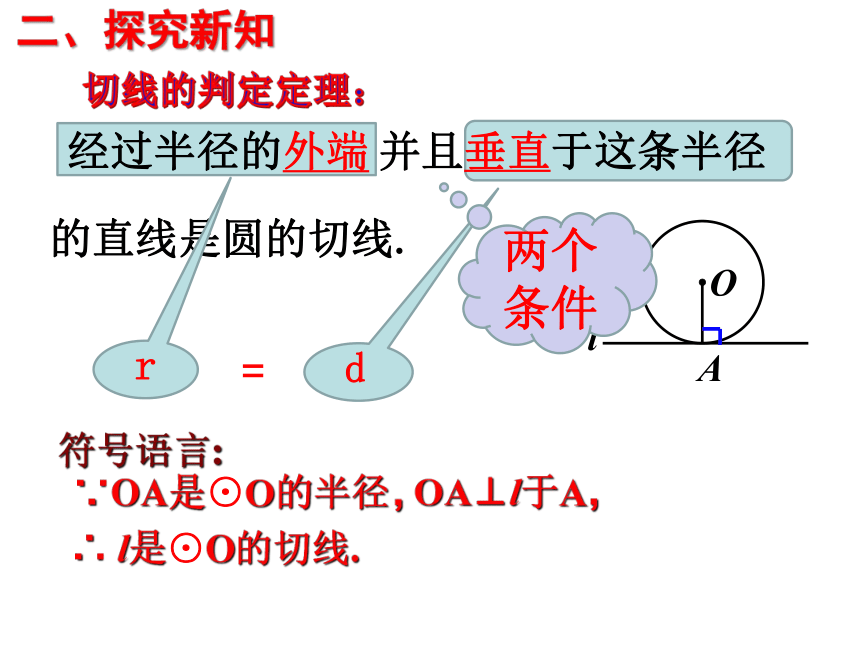
条件一: 经过半径OA的外端点A;
条件二: 垂直于半径OA.
结论:直线l是⊙O的切线.
A
O
l
直线l满足
二、探究新知
说一说
A
O
l
经过半径的外端
切线的判定定理:
的直线是圆的切线.
并且垂直于这条半径
符号语言:
∵OA是⊙O的半径,
∴ l是⊙O的切线.
d
r
=
二、探究新知
OA⊥l于A,
两个
条件
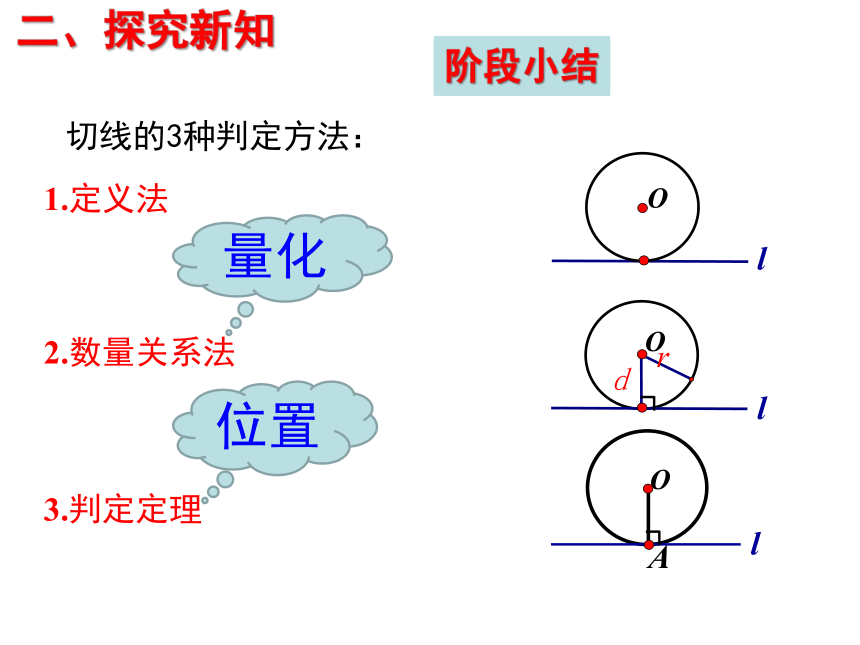
1.定义法
2.数量关系法
3.判定定理
A
l
O
切线的3种判定方法:
阶段小结
二、探究新知
量化
位置
l
O
l
r
d
O
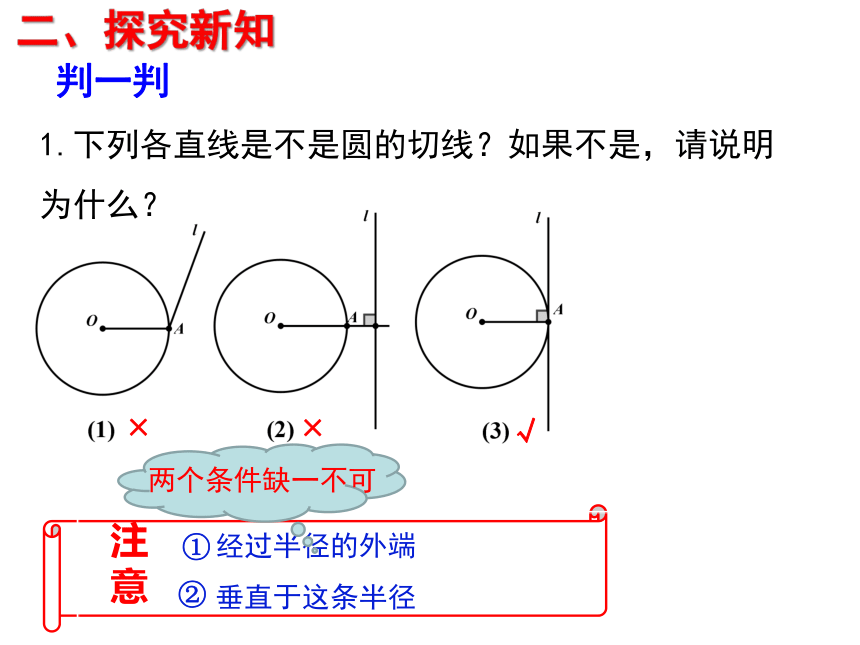
判一判
1.下列各直线是不是圆的切线?如果不是,请说明为什么?
经过半径的外端
垂直于这条半径
注意
①
②
两个条件缺一不可
√
二、探究新知
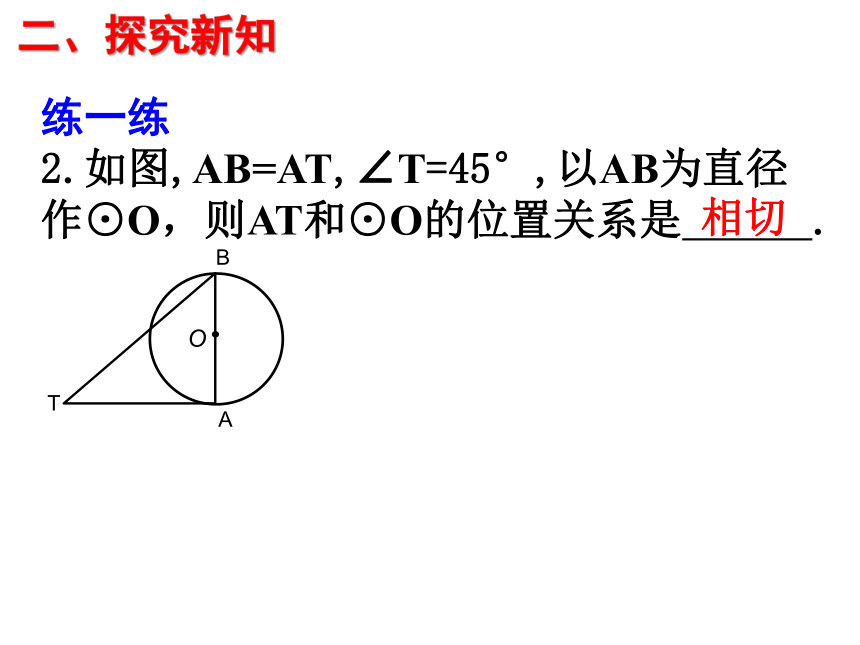
练一练
2.如图,AB=AT,∠T=45°,以AB为直径
作⊙O,则AT和⊙O的位置关系是 .
相切
二、探究新知
A
B
T
O
.
探究二 切线性质定理
A
l
O
二、探究新知
∵OA是⊙O的半径,
OA⊥l于A,
l是⊙O的切线.
切线判定定理
如果直线 是⊙O的切线,切点为A,
那么半径OA与直线 是不是一定垂直呢?
l
l
∴
圆的切线垂直于过切点的半径.
符号语言:
∵l与 ⊙O相切于点A,
A
l
O
切线的性质定理:
∴OA⊥l .
二、探究新知
.
A
B
3.如图,AB是⊙O的直径,直线 ,
线,A ,B是切点,则 , 的位置是 .
平行
⊙O的切
二、探究新知
4.如图,PA是半径为2的⊙O的切线,切点为A,∠P= ,那么OP= .
练一练
O
P
A
(
30°
4
见切线,连半径,得垂直.
例题 已知:直线BC经过⊙O上的点D ,
并且OB=OC,BD=CD.
求证:直线BC是⊙O的切线.
O
C
B
D
证明:连接OD.
∵ OB=OC,BD=CD,
∴ BC⊥OD.
∵OD是⊙O的半径,
∴ BC是⊙O的切线.
三、合作探究
变式 如图,△ABC为等腰三角形,O是底边BC中线 所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
例题 已知:直线BC经过⊙O上的点D,并且OB=OC, BD=CD.
求证:直线BC是⊙O的切线.
D
A
.
O
三、合作探究
证明:过O 作OE ⊥AC于E , 连接OA,OD .
∵☉O 与AB 相切于D , ∴OD⊥ AB.
∵AB =AC ,O是底边BC中线所在直线上的一点,
∴AO 平分∠BAC .
∴OE=OD,即OE是☉O的半径.
∴AC 是☉O 的切线.
又OD ⊥AB ,OE⊥AC.
变式 如图,△ABC为等腰三角形,O是底边BC中线所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
E
B
O
C
D
A
.
三、合作探究
E
B
O
C
D
A
例题如图,直线BC经过⊙O上的点D,并且OB=OC,BD=CD.
求证:直线BC是⊙O的切线.
O
C
B
D
变式如图,△ABC为等腰三角形,O是底边BC中线所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
对比归纳
连接
作垂直
有交点,连半径,证垂直
无交点,作垂直,证半径
证明切线的方法
三、合作探究
证切线
转化
证线段相等
证切线
转化
证垂直
四、反思归纳
1.通过本节课的学习,你有哪些收获?
知识
方法
思想
判定定理
性质定理
有交点
连半径
证垂直
无交点
作垂直
证半径
见切线
连半径
得垂直
数形
结合
转化
切线的
判定与
性 质
四、反思归纳
2.对于切线的判定定理和性质定理,我们是如何研究学习的?
画 一 画
想 一 想
议 一 议
说 一 说
找 一 找
判 一 判
练 一 练
定理学习基本过程
实验操作
观察发现
证明猜想
形成定理
剖析定理
理解定理
运用定理
必做题:教科书第101页第4、5题.
选做题:教科书第102页第12题.
五、课后作业
知识像一艘船
让它载着我们
驶向理想的
……
谢谢
人教版九年级数学上册
24.2 切线的判定与性质
第24章 圆
1.下雨天当你快速转动雨伞时飞出的雨珠,它们运动的轨迹是一条什么线?
一、情境引入
o
取其中的一条射线,这条射线所在的直线为 ,直线 与
圆有什么位置关系?
定义法
2.若雨伞外边沿所在圆的半径r为50cm,
圆心O直线 l 的距离d=50cm,此时直线l和
⊙O的位置关系是 .
相切
d=r
切线
一、情境引入
o
d
数
形
数量关系法
数形结合
探究一 切线的判定定理
想一想
直线l和⊙O有什么位置关系?
你判断的依据是什么呢?
画一画 在学案上画一个⊙O,在圆上取一点A,连接OA,经过半径OA的外端点A作直线l ⊥OA.
O
A
l
议一议
直线l满足什么条件时,它是⊙O的切线? 由此你能得到什么结论?
.
二、探究新知
条件一: 经过半径OA的外端点A;
条件二: 垂直于半径OA.
结论:直线l是⊙O的切线.
A
O
l
直线l满足
二、探究新知
说一说
A
O
l
经过半径的外端
切线的判定定理:
的直线是圆的切线.
并且垂直于这条半径
符号语言:
∵OA是⊙O的半径,
∴ l是⊙O的切线.
d
r
=
二、探究新知
OA⊥l于A,
两个
条件
1.定义法
2.数量关系法
3.判定定理
A
l
O
切线的3种判定方法:
阶段小结
二、探究新知
量化
位置
l
O
l
r
d
O
判一判
1.下列各直线是不是圆的切线?如果不是,请说明为什么?
经过半径的外端
垂直于这条半径
注意
①
②
两个条件缺一不可
√
二、探究新知
练一练
2.如图,AB=AT,∠T=45°,以AB为直径
作⊙O,则AT和⊙O的位置关系是 .
相切
二、探究新知
A
B
T
O
.
探究二 切线性质定理
A
l
O
二、探究新知
∵OA是⊙O的半径,
OA⊥l于A,
l是⊙O的切线.
切线判定定理
如果直线 是⊙O的切线,切点为A,
那么半径OA与直线 是不是一定垂直呢?
l
l
∴
圆的切线垂直于过切点的半径.
符号语言:
∵l与 ⊙O相切于点A,
A
l
O
切线的性质定理:
∴OA⊥l .
二、探究新知
.
A
B
3.如图,AB是⊙O的直径,直线 ,
线,A ,B是切点,则 , 的位置是 .
平行
⊙O的切
二、探究新知
4.如图,PA是半径为2的⊙O的切线,切点为A,∠P= ,那么OP= .
练一练
O
P
A
(
30°
4
见切线,连半径,得垂直.
例题 已知:直线BC经过⊙O上的点D ,
并且OB=OC,BD=CD.
求证:直线BC是⊙O的切线.
O
C
B
D
证明:连接OD.
∵ OB=OC,BD=CD,
∴ BC⊥OD.
∵OD是⊙O的半径,
∴ BC是⊙O的切线.
三、合作探究
变式 如图,△ABC为等腰三角形,O是底边BC中线 所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
例题 已知:直线BC经过⊙O上的点D,并且OB=OC, BD=CD.
求证:直线BC是⊙O的切线.
D
A
.
O
三、合作探究
证明:过O 作OE ⊥AC于E , 连接OA,OD .
∵☉O 与AB 相切于D , ∴OD⊥ AB.
∵AB =AC ,O是底边BC中线所在直线上的一点,
∴AO 平分∠BAC .
∴OE=OD,即OE是☉O的半径.
∴AC 是☉O 的切线.
又OD ⊥AB ,OE⊥AC.
变式 如图,△ABC为等腰三角形,O是底边BC中线所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
E
B
O
C
D
A
.
三、合作探究
E
B
O
C
D
A
例题如图,直线BC经过⊙O上的点D,并且OB=OC,BD=CD.
求证:直线BC是⊙O的切线.
O
C
B
D
变式如图,△ABC为等腰三角形,O是底边BC中线所在直线上的一点,腰AB与⊙O相切于D.
求证:AC是⊙O的切线.
对比归纳
连接
作垂直
有交点,连半径,证垂直
无交点,作垂直,证半径
证明切线的方法
三、合作探究
证切线
转化
证线段相等
证切线
转化
证垂直
四、反思归纳
1.通过本节课的学习,你有哪些收获?
知识
方法
思想
判定定理
性质定理
有交点
连半径
证垂直
无交点
作垂直
证半径
见切线
连半径
得垂直
数形
结合
转化
切线的
判定与
性 质
四、反思归纳
2.对于切线的判定定理和性质定理,我们是如何研究学习的?
画 一 画
想 一 想
议 一 议
说 一 说
找 一 找
判 一 判
练 一 练
定理学习基本过程
实验操作
观察发现
证明猜想
形成定理
剖析定理
理解定理
运用定理
必做题:教科书第101页第4、5题.
选做题:教科书第102页第12题.
五、课后作业
知识像一艘船
让它载着我们
驶向理想的
……
谢谢
同课章节目录
