2021-2022学年人教版八年级数学上册15.1.2分式的基本性质 课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册15.1.2分式的基本性质 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第十五章 分式
15.1.2 分式的基本性质
15.1 分式
学习目标
1
2
理解并掌握分式的基质.
理解最简分式和最简公分母的概念.
会用分式的基本性质进行分式的约分和通分.
3
温故知新
1.分式的概念
2.分式有无意义和值为0的条件
(1)当分式中的B≠0时,分式有意义 ;
(2)当分式中的B=0时,分式意义 ;
(3)当分式中的B≠0,A=0时,分式的值为0.
把除式 A÷B 写成 的形式,其中 A,B 都是整式,且 B 中含有字母,我们把代数式 叫做分式.
【思考】下列两式成立吗?为什么?
新课导入
(2)
(1)
依据:分数的基本性质
分数的分子与分母同时乘(或除以)一个不等于0的数,分数的值不变.
用字母表示:
对于任意一个分数 有:
2.类比分数的基本性质,你能猜想分式有什么性质吗?怎样用式子的形式表示出来?
【思考】
1.你认为分式 与 ,分式 与 相等吗?(a、m、n均不为0)
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
上述性质可以用式子表示为:
其中A、B、C是整式.
分式的基本性质:
知识讲解
(1)分子、分母应同时做乘、除法中的同一种运算;
(2)所乘(或除以)的必须是同一个整式;
(3)所乘(或除以)的整式应该不等于零.
追问 应用分式的基本性质时需要注意什么?
归纳:看分母如何变化,想分子如何变化.
看分子如何变化,想分母如何变化.
分式基本性质应用
判断正误:
( ) ( )
( ) ( )
×
×
√
√
( )
( )
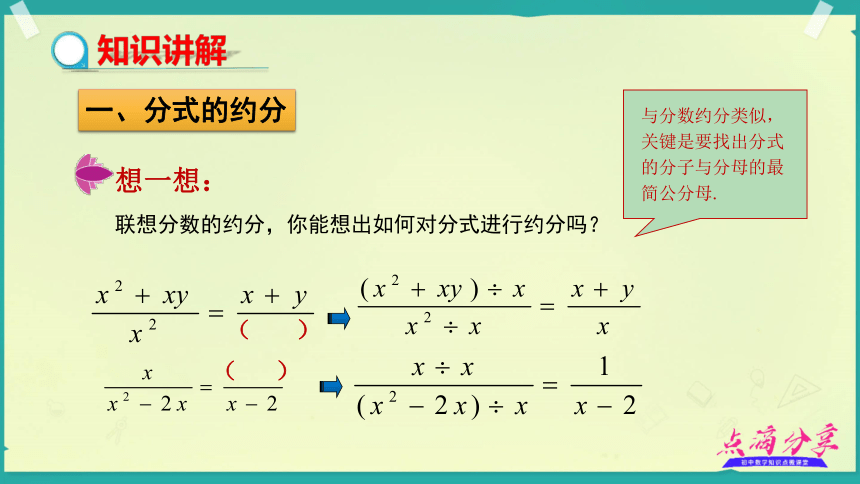
与分数约分类似,关键是要找出分式的分子与分母的最简公分母.
一、分式的约分
知识讲解
想一想:
联想分数的约分,你能想出如何对分式进行约分吗?
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
经过约分后的分式 ,其分子与分母没有公因式.像这样,分子与分母没有公因式的式子,叫做最简分式.
约分的概念:
最简分式的概念:
例 约分:
分析:(1)中,分子、分母的公因式是 ;
(2)中,可以将分母分解因式为 ;
(3)中,可以将分子分解因式为 ;
5abc
(x+3)2
6(x-y)2
解:
试一试: 对 进行通分
12与8的最小公倍数:24.
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分.
通分的关键是确定几个
分母的最小公倍数.
二、分式的通分
与分数的通分类似,根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。
分式的通分:
确定最简公分母的方法:
若分子或分母含多项式时,要先进行因式分解
(1)系数:分式分母系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都要取到;
(3)因式的指数:相同因式去指数最高的.
最简公分母
通分:
解:(1)最简公分母是2a2b2c.
例1
不同的因式
最简公分母
1·(x-5)
(x-5)
1·(x+5)
1
(x+5)
(2)最简公分母是(x+5)(x-5).
通分:
(x+y)(x-y)
解:最简公分母是x(x+y)(x-y).
x(x+y)
例2
课堂小结
1、分数的基本性质
分数的分子与分母同时乘(或除以)一个不等于0的数,分数的值不变.
2、分式的符号法则
分式的分子、分母与分式本身的符号,同时改变其中两个,分式的值不变。
课堂小结
1.约分
2.通分
最简分式或整式
结果
关键
确定最简公分母
若分子或分母含多项式时,要先进行因式分解.
3.确定最简公分母的方法
找出分子和分母的公因式.
若分子或分母是多项式, 则先进行
因式分解,再找出分子和分母的公
因式进行约分.
第十五章 分式
15.1.2 分式的基本性质
15.1 分式
学习目标
1
2
理解并掌握分式的基质.
理解最简分式和最简公分母的概念.
会用分式的基本性质进行分式的约分和通分.
3
温故知新
1.分式的概念
2.分式有无意义和值为0的条件
(1)当分式中的B≠0时,分式有意义 ;
(2)当分式中的B=0时,分式意义 ;
(3)当分式中的B≠0,A=0时,分式的值为0.
把除式 A÷B 写成 的形式,其中 A,B 都是整式,且 B 中含有字母,我们把代数式 叫做分式.
【思考】下列两式成立吗?为什么?
新课导入
(2)
(1)
依据:分数的基本性质
分数的分子与分母同时乘(或除以)一个不等于0的数,分数的值不变.
用字母表示:
对于任意一个分数 有:
2.类比分数的基本性质,你能猜想分式有什么性质吗?怎样用式子的形式表示出来?
【思考】
1.你认为分式 与 ,分式 与 相等吗?(a、m、n均不为0)
分式的分子与分母乘(或除以)同一个不等于0的整式,分式的值不变.
上述性质可以用式子表示为:
其中A、B、C是整式.
分式的基本性质:
知识讲解
(1)分子、分母应同时做乘、除法中的同一种运算;
(2)所乘(或除以)的必须是同一个整式;
(3)所乘(或除以)的整式应该不等于零.
追问 应用分式的基本性质时需要注意什么?
归纳:看分母如何变化,想分子如何变化.
看分子如何变化,想分母如何变化.
分式基本性质应用
判断正误:
( ) ( )
( ) ( )
×
×
√
√
( )
( )
与分数约分类似,关键是要找出分式的分子与分母的最简公分母.
一、分式的约分
知识讲解
想一想:
联想分数的约分,你能想出如何对分式进行约分吗?
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
经过约分后的分式 ,其分子与分母没有公因式.像这样,分子与分母没有公因式的式子,叫做最简分式.
约分的概念:
最简分式的概念:
例 约分:
分析:(1)中,分子、分母的公因式是 ;
(2)中,可以将分母分解因式为 ;
(3)中,可以将分子分解因式为 ;
5abc
(x+3)2
6(x-y)2
解:
试一试: 对 进行通分
12与8的最小公倍数:24.
分数的通分:把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分.
通分的关键是确定几个
分母的最小公倍数.
二、分式的通分
与分数的通分类似,根据分式的基本性质,把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做分式的通分。
分式的通分:
确定最简公分母的方法:
若分子或分母含多项式时,要先进行因式分解
(1)系数:分式分母系数的最小公倍数;
(2)因式:凡各分母中出现的不同因式都要取到;
(3)因式的指数:相同因式去指数最高的.
最简公分母
通分:
解:(1)最简公分母是2a2b2c.
例1
不同的因式
最简公分母
1·(x-5)
(x-5)
1·(x+5)
1
(x+5)
(2)最简公分母是(x+5)(x-5).
通分:
(x+y)(x-y)
解:最简公分母是x(x+y)(x-y).
x(x+y)
例2
课堂小结
1、分数的基本性质
分数的分子与分母同时乘(或除以)一个不等于0的数,分数的值不变.
2、分式的符号法则
分式的分子、分母与分式本身的符号,同时改变其中两个,分式的值不变。
课堂小结
1.约分
2.通分
最简分式或整式
结果
关键
确定最简公分母
若分子或分母含多项式时,要先进行因式分解.
3.确定最简公分母的方法
找出分子和分母的公因式.
若分子或分母是多项式, 则先进行
因式分解,再找出分子和分母的公
因式进行约分.
