2021-2022学年人教版九年级数学下册第二十六章反比例函数大整合课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十六章反比例函数大整合课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 349.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 23:42:37 | ||
图片预览








文档简介
(共21张PPT)
26章反比例函数大整合
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
反比例函数解析式
反比例函数图像与性质
实际问题与反比例函数
反比例函数与一次函数
知识点框架
02
知识点框架
反比例函数的定义
一般地,函数 (k是常数,k≠0)叫做反比例函数。
反比例函数的解析式也可以写成y=kx-1或xy=k的形式。
自变量x的取值范围是x≠0的一切实数,函数的取值范围也是一切非零实数。
反比例函数的图像
反比例函数图象“曲线”及“两支”的特征.(即双曲线)反比例函数(k≠0)的图象中两支曲线都与x轴、y轴不相交;并且当k>0时,图象在第一、第三象限内,函数值y随自变量x取值的增大而减小:当k<0时,图象在第二、第四象限内,函数值y随自变量x取值的增大而增大。
知识点框架
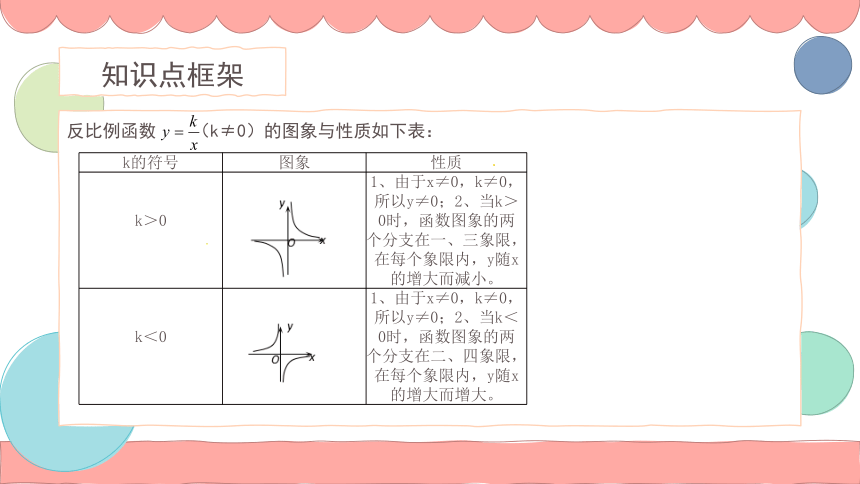
反比例函数 (k≠0)的图象与性质如下表:
k的符号 图象 性质
k>0 1、由于x≠0,k≠0,所以y≠0;2、当k>0时,函数图象的两个分支在一、三象限,在每个象限内,y随x的增大而减小。
k<0 1、由于x≠0,k≠0,所以y≠0;2、当k<0时,函数图象的两个分支在二、四象限,在每个象限内,y随x的增大而增大。
知识点框架
反比例函数图像的性质
(1).对称性:反比例函数 (k≠0)的图象关于直角坐标系的原点成中心对称。
反比例函数 与 (k≠0)的图象关于直角坐标系的x轴成轴对称。
(2).反比例函数 (k≠0)中的比例系数k的几何意义。
过双曲线上任一点作x轴、y轴的垂线PM、PN,所得矩形PMON的面积
∵ (k≠0)
∴k=xy ∴
即过双曲线上任意一点作x轴、y轴的垂线,与原点O所得矩形的面积为|k|
知识点框架
实际问题与反比例函数
(1)能灵活运用反比例函数的知识解决实际问题;
(2)经历“实际问题——建立模型——拓展应用”的过程,培养分析问题,解决问题的能力
例题练习
03
作业布置
04
作业布置
7.已知直线y=-x+7与反比例函数y= (k>0, x>0)交于A、B两点,与坐标轴交于C、D两点,若S△BOC= ,且∠AOD=∠BOC.
(1)求反比例函数的解析式;
(2)求证:OA=OB;
(3)y= (k>0, x>0)的图象上是否存在点P,使 S△AOP=S△BOP,若存在,
求P点的坐标,若不存在,说明理由.
D
C
_
B
A
O
x
y
下节课见!
26章反比例函数大整合
目录
01
教学目标
02
知识点框架
03
例题练习
04
作业布置
教学目标
01
教学目标
反比例函数解析式
反比例函数图像与性质
实际问题与反比例函数
反比例函数与一次函数
知识点框架
02
知识点框架
反比例函数的定义
一般地,函数 (k是常数,k≠0)叫做反比例函数。
反比例函数的解析式也可以写成y=kx-1或xy=k的形式。
自变量x的取值范围是x≠0的一切实数,函数的取值范围也是一切非零实数。
反比例函数的图像
反比例函数图象“曲线”及“两支”的特征.(即双曲线)反比例函数(k≠0)的图象中两支曲线都与x轴、y轴不相交;并且当k>0时,图象在第一、第三象限内,函数值y随自变量x取值的增大而减小:当k<0时,图象在第二、第四象限内,函数值y随自变量x取值的增大而增大。
知识点框架
反比例函数 (k≠0)的图象与性质如下表:
k的符号 图象 性质
k>0 1、由于x≠0,k≠0,所以y≠0;2、当k>0时,函数图象的两个分支在一、三象限,在每个象限内,y随x的增大而减小。
k<0 1、由于x≠0,k≠0,所以y≠0;2、当k<0时,函数图象的两个分支在二、四象限,在每个象限内,y随x的增大而增大。
知识点框架
反比例函数图像的性质
(1).对称性:反比例函数 (k≠0)的图象关于直角坐标系的原点成中心对称。
反比例函数 与 (k≠0)的图象关于直角坐标系的x轴成轴对称。
(2).反比例函数 (k≠0)中的比例系数k的几何意义。
过双曲线上任一点作x轴、y轴的垂线PM、PN,所得矩形PMON的面积
∵ (k≠0)
∴k=xy ∴
即过双曲线上任意一点作x轴、y轴的垂线,与原点O所得矩形的面积为|k|
知识点框架
实际问题与反比例函数
(1)能灵活运用反比例函数的知识解决实际问题;
(2)经历“实际问题——建立模型——拓展应用”的过程,培养分析问题,解决问题的能力
例题练习
03
作业布置
04
作业布置
7.已知直线y=-x+7与反比例函数y= (k>0, x>0)交于A、B两点,与坐标轴交于C、D两点,若S△BOC= ,且∠AOD=∠BOC.
(1)求反比例函数的解析式;
(2)求证:OA=OB;
(3)y= (k>0, x>0)的图象上是否存在点P,使 S△AOP=S△BOP,若存在,
求P点的坐标,若不存在,说明理由.
D
C
_
B
A
O
x
y
下节课见!
