2021—2022学年北师大版数学九年级下册2.4.1二次函数的应用(一)课件(共21张PPT)
文档属性
| 名称 | 2021—2022学年北师大版数学九年级下册2.4.1二次函数的应用(一)课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:31:58 | ||
图片预览






文档简介
(共21张PPT)
第二章 二次函数
2.4. 1二次函数的应用(一)
温故知新
顶点式
开口方向:
对称轴:
顶点坐标:
x = h
(h,k)
y = a( x - h )2 + k
a>0
a<0
开口向上
开口向下
当x=h时,
函数y有最大(最小)值k
温故知新
二次函数一般式:
对称轴是:
顶点坐标是:
b
2a
-
,
4ac-b
4a
)
(
b
2a
-
x=
直线
函数y有最大(最小)值
4ac-b
4a
时,
x=-
b
2a
当
开口方向:
a>0
a<0
开口向上
开口向下
y=ax +bx+c
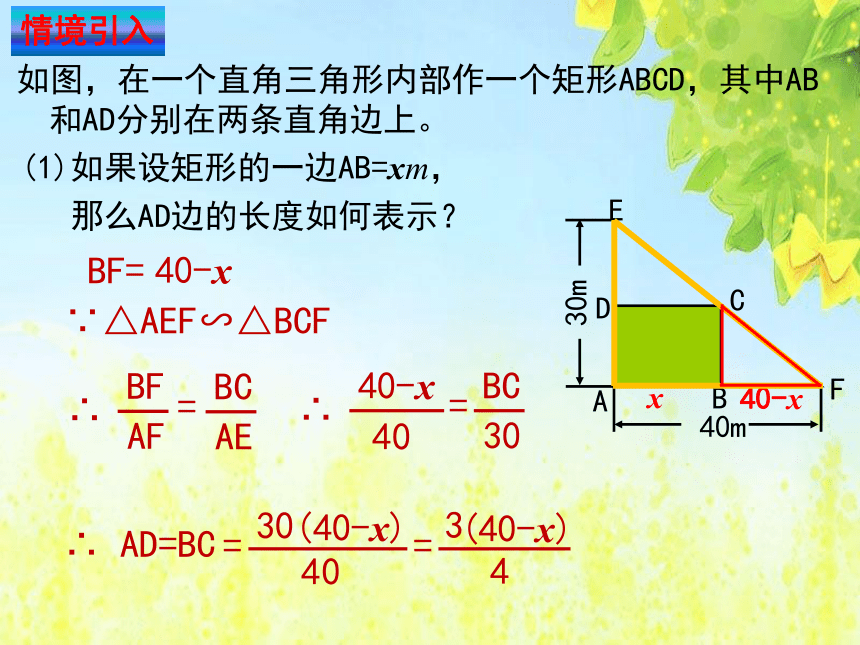
如图,在一个直角三角形内部作一个矩形ABCD,其中AB和AD分别在两条直角边上。
30m
40m
A
B
C
D
E
F
(1)如果设矩形的一边AB=xm,
∵△AEF∽△BCF
40-x
x
40-x
那么AD边的长度如何表示?
情境引入
BF=
BF
AF
BC
AE
=
∴
40-x
40
BC
30
=
∴
∴ AD=BC
30
(40-x)
40
=
=
3
(40-x)
4
情境引入
(2)设矩形的面积为ym2,y与x有怎样的函数关系?
30m
40m
A
B
C
D
E
F
x
=
3
(40-x)
4
AD
∴y =
3
(40-x)
4
x
·
∵S矩形ABCD=AB×AD
整理得:
y = x2+30x
-
3
4
自变量x的取值有限制吗?
0<
x<40
新知探究
(3)当x取何值时,y有值最大,最大值是多少?
30m
40m
A
B
C
D
E
F
x
y = x2+30x
-
3
4
化为顶点式,得
所以,当x取20m时,
y有最大值
最大值是300m2.
y = (x -20)2+300
-
3
4
b
2a
-
4ac-b
4a
新知探究
二次函数的应用(最值)
1、根据题意列出二次函数表达式;
2、将二次函数表达式化成顶点式
3、确定最值:
若a>0,
若a<0,
当x=h时,y最小=k;
当x=h时,y最大=k。
(或利用顶点公式)
新知探究
A
B
C
D
30m
40m
E
F
G
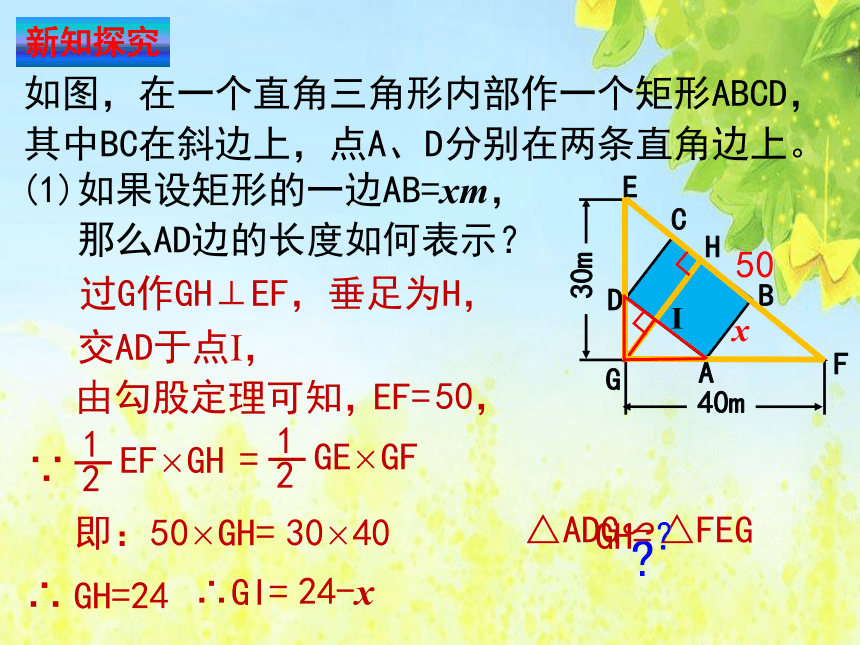
如图,在一个直角三角形内部作一个矩形ABCD,其中BC在斜边上,点A、D分别在两条直角边上。
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
x
H
I
└
└
过G作GH⊥EF,垂足为H,
由勾股定理可知,
∴GI=
交AD于点I,
∴ GH=24
EF×GH
1
2
∵
GE×GF
1
2
=
即:50×GH= 30×40
50
EF=
50,
24-x
△ADG∽△FEG
GH=?
新知探究
A
B
C
D
30m
40m
E
F
G
x
└
└
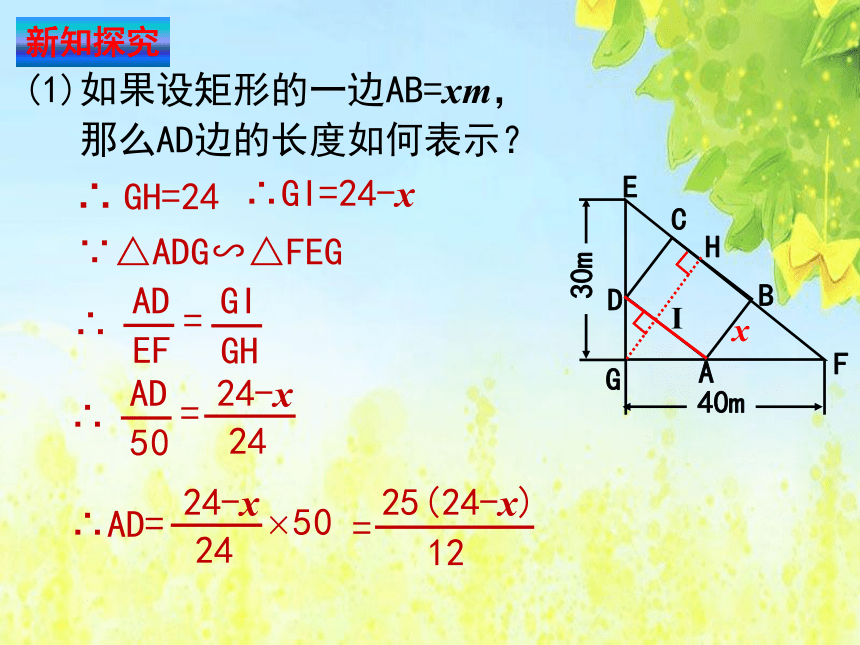
∵△ADG∽△FEG
∴GI=24-x
∴ GH=24
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
AD
EF
GI
GH
=
∴
AD
50
24-x
24
=
∴
∴AD=
24-x
24
×50
=
25(24-x)
12
H
I
新知探究
(2)设矩形的面积为ym2,y与x有怎样的函数关系?
∵AB=xm,
且S矩形ABCD =
整理得:
自变量x的取值有没有限制?
A
B
C
D
30m
40m
E
F
G
x
└
└
AD
=
25(24-x)
12
∴y =
x
·
25(24-x)
12
y = x2+50x
-
25
12
0<
AD
=
25(24-x)
12
x<24
AB×AD
新知探究
(3)当x取何值时,y有值最大,最大值是多少?
所以,当x取12时,
y有值最大,
最大值是300m2.
y = x2+50x
-
25
12
化顶点式,得
y = x2+50x
-
25
12
把
y = (x -12)2+300
-
25
12
新知探究
例1、某建筑物窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗户的材料总长(图中所有黑线的总和)为15m,当x等于多少时,窗户通过的光线最多 (结果精确到0.01m)此时,窗户的面积是多少 (结果精确到0.01m)
x
解:
+4y
+πx
=15
7x
∴y =
15-7x-πx
4
2x
设窗户的面积为Sm2,
S =
1
2
πx
+2xy
=
1
2
πx
15-7x-πx
4
+2x
·
新知探究
此时,窗户的面积约为4.02m2.
S =
15-7x-πx
4
2x
·
整理得:
S = x2+ x
-
7
2
15
2
x
2x
S = (x )2
-
7
2
-
15
14
+
225
56
当x=
15
14
≈1.07时,
S最大 =
225
56
≈4.02
窗户通过的光线最多,
所以当x约为1.07m时,
归纳
利用二次函数解决实际问题基本思路
(1)分析问题中的变量和常量,
(2)用数学的方式表示它们之间的关系;
搞清它们之间的关系;
(4)检验结果的合理性。
(3)利用二次函数相关知识求解;
练一练
1.在一长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm ,设金色纸边的宽度为xcm,
那么y关于x的函数是( )
A. y=(60+2x)(40+2x)
B. y =(60+x)(40+x)
C. y =(60+2x)(40+x)
D. y =(60+x)(40+2x)
A
练一练
2.下列函数中,当x>0时,y值随x值的增大而减
小的是( )
D.y=x
B.y=2x-1
C.y=
1
x
A. y=x
C
练一练
3.军事演习时发射一颗炮弹,经xs后炮弹的高度为ym,且时间x(s)与高度y(m)之间的函数关系为y=ax +bx(a≠0),若炮弹在第8s与第14s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9s
B.第11s
C.第13s
D.第15s
B
x
O
8 14
y
练一练
2.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门.已知计划中的建筑
材料可建围墙(不包括门)的
总长度为50m,设饲养长为
x(m),占地面积为y(m ),则
y关于x的函数表达式是( )
A.y=-x +50x
B.y=- x +24x
1
2
C.y=- x +25x
1
2
D.y=- x +26x
1
2
D
练一练
如图,在一个直角三角形内部作一个矩形ABCD,其中AB和AD分别在两条直角边上。设矩形的一边AD=xm,矩形的面积为ym2,当x取何值时, y有值最大,最大值是多少?
30m
40m
A
B
C
D
E
F
x
课堂小结
利用二次函数解决实际问题基本思路
(1)分析问题中的变量和常量,
(2)用数学的方式表示它们之间的关系;
搞清它们之间的关系;
(4)检验结果的合理性。
(3)利用二次函数相关知识求解;
作业
P47-48
1,2,3,
第二章 二次函数
2.4. 1二次函数的应用(一)
温故知新
顶点式
开口方向:
对称轴:
顶点坐标:
x = h
(h,k)
y = a( x - h )2 + k
a>0
a<0
开口向上
开口向下
当x=h时,
函数y有最大(最小)值k
温故知新
二次函数一般式:
对称轴是:
顶点坐标是:
b
2a
-
,
4ac-b
4a
)
(
b
2a
-
x=
直线
函数y有最大(最小)值
4ac-b
4a
时,
x=-
b
2a
当
开口方向:
a>0
a<0
开口向上
开口向下
y=ax +bx+c
如图,在一个直角三角形内部作一个矩形ABCD,其中AB和AD分别在两条直角边上。
30m
40m
A
B
C
D
E
F
(1)如果设矩形的一边AB=xm,
∵△AEF∽△BCF
40-x
x
40-x
那么AD边的长度如何表示?
情境引入
BF=
BF
AF
BC
AE
=
∴
40-x
40
BC
30
=
∴
∴ AD=BC
30
(40-x)
40
=
=
3
(40-x)
4
情境引入
(2)设矩形的面积为ym2,y与x有怎样的函数关系?
30m
40m
A
B
C
D
E
F
x
=
3
(40-x)
4
AD
∴y =
3
(40-x)
4
x
·
∵S矩形ABCD=AB×AD
整理得:
y = x2+30x
-
3
4
自变量x的取值有限制吗?
0<
x<40
新知探究
(3)当x取何值时,y有值最大,最大值是多少?
30m
40m
A
B
C
D
E
F
x
y = x2+30x
-
3
4
化为顶点式,得
所以,当x取20m时,
y有最大值
最大值是300m2.
y = (x -20)2+300
-
3
4
b
2a
-
4ac-b
4a
新知探究
二次函数的应用(最值)
1、根据题意列出二次函数表达式;
2、将二次函数表达式化成顶点式
3、确定最值:
若a>0,
若a<0,
当x=h时,y最小=k;
当x=h时,y最大=k。
(或利用顶点公式)
新知探究
A
B
C
D
30m
40m
E
F
G
如图,在一个直角三角形内部作一个矩形ABCD,其中BC在斜边上,点A、D分别在两条直角边上。
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
x
H
I
└
└
过G作GH⊥EF,垂足为H,
由勾股定理可知,
∴GI=
交AD于点I,
∴ GH=24
EF×GH
1
2
∵
GE×GF
1
2
=
即:50×GH= 30×40
50
EF=
50,
24-x
△ADG∽△FEG
GH=?
新知探究
A
B
C
D
30m
40m
E
F
G
x
└
└
∵△ADG∽△FEG
∴GI=24-x
∴ GH=24
(1)如果设矩形的一边AB=xm,
那么AD边的长度如何表示?
AD
EF
GI
GH
=
∴
AD
50
24-x
24
=
∴
∴AD=
24-x
24
×50
=
25(24-x)
12
H
I
新知探究
(2)设矩形的面积为ym2,y与x有怎样的函数关系?
∵AB=xm,
且S矩形ABCD =
整理得:
自变量x的取值有没有限制?
A
B
C
D
30m
40m
E
F
G
x
└
└
AD
=
25(24-x)
12
∴y =
x
·
25(24-x)
12
y = x2+50x
-
25
12
0<
AD
=
25(24-x)
12
x<24
AB×AD
新知探究
(3)当x取何值时,y有值最大,最大值是多少?
所以,当x取12时,
y有值最大,
最大值是300m2.
y = x2+50x
-
25
12
化顶点式,得
y = x2+50x
-
25
12
把
y = (x -12)2+300
-
25
12
新知探究
例1、某建筑物窗户如图所示,它的上半部分是半圆,下半部分是矩形,制造窗户的材料总长(图中所有黑线的总和)为15m,当x等于多少时,窗户通过的光线最多 (结果精确到0.01m)此时,窗户的面积是多少 (结果精确到0.01m)
x
解:
+4y
+πx
=15
7x
∴y =
15-7x-πx
4
2x
设窗户的面积为Sm2,
S =
1
2
πx
+2xy
=
1
2
πx
15-7x-πx
4
+2x
·
新知探究
此时,窗户的面积约为4.02m2.
S =
15-7x-πx
4
2x
·
整理得:
S = x2+ x
-
7
2
15
2
x
2x
S = (x )2
-
7
2
-
15
14
+
225
56
当x=
15
14
≈1.07时,
S最大 =
225
56
≈4.02
窗户通过的光线最多,
所以当x约为1.07m时,
归纳
利用二次函数解决实际问题基本思路
(1)分析问题中的变量和常量,
(2)用数学的方式表示它们之间的关系;
搞清它们之间的关系;
(4)检验结果的合理性。
(3)利用二次函数相关知识求解;
练一练
1.在一长60cm,宽40cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是ycm ,设金色纸边的宽度为xcm,
那么y关于x的函数是( )
A. y=(60+2x)(40+2x)
B. y =(60+x)(40+x)
C. y =(60+2x)(40+x)
D. y =(60+x)(40+2x)
A
练一练
2.下列函数中,当x>0时,y值随x值的增大而减
小的是( )
D.y=x
B.y=2x-1
C.y=
1
x
A. y=x
C
练一练
3.军事演习时发射一颗炮弹,经xs后炮弹的高度为ym,且时间x(s)与高度y(m)之间的函数关系为y=ax +bx(a≠0),若炮弹在第8s与第14s时的高度相等,则在下列哪一个时间的高度是最高的( )
A.第9s
B.第11s
C.第13s
D.第15s
B
x
O
8 14
y
练一练
2.某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),并在如图所示位置留2m宽的门.已知计划中的建筑
材料可建围墙(不包括门)的
总长度为50m,设饲养长为
x(m),占地面积为y(m ),则
y关于x的函数表达式是( )
A.y=-x +50x
B.y=- x +24x
1
2
C.y=- x +25x
1
2
D.y=- x +26x
1
2
D
练一练
如图,在一个直角三角形内部作一个矩形ABCD,其中AB和AD分别在两条直角边上。设矩形的一边AD=xm,矩形的面积为ym2,当x取何值时, y有值最大,最大值是多少?
30m
40m
A
B
C
D
E
F
x
课堂小结
利用二次函数解决实际问题基本思路
(1)分析问题中的变量和常量,
(2)用数学的方式表示它们之间的关系;
搞清它们之间的关系;
(4)检验结果的合理性。
(3)利用二次函数相关知识求解;
作业
P47-48
1,2,3,
