2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2 指数函数(指数函数的概念+指数函数的图像和性质) 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册4.2 指数函数(指数函数的概念+指数函数的图像和性质) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 47.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 15:50:17 | ||
图片预览








文档简介
(共24张PPT)
第4章 指数函数与对数函数
4.2 指数函数
导问:创设情境,引入主题
给我一个支点,我能够撬动地球。
----阿基米德
给我一张足够大的纸,我能够上月球,你信吗?
给你一张纸,你能折几次呢?
导问:创设情境,引入主题
如果你有一张面积无限、强度无限,厚度为0.01毫米的纸,如果折叠能力无限,那么多次对折,纸张的厚度会变成多少呢?
导问:创设情境,引入主题
问题1:一张薄薄的纸,却折叠出了惊天的气势,蕴含着神奇的数学知识。若把纸张的初始厚度设为1,经过x次对折后, 纸张厚度y与对折次数x之间的关系是什么?
对折次数 纸张厚度
0 1
1
2
3
··· ···
导问:创设情境,引入主题
每折叠一次,得到的纸张的厚度都约为前一次的2倍.也就是每次的厚度相比于折叠之前都增长了100%,我们称这个100%为增长率。
增长率为常数的变化方式,我们称为指数增长。
0 1
1
2
3
··· ···
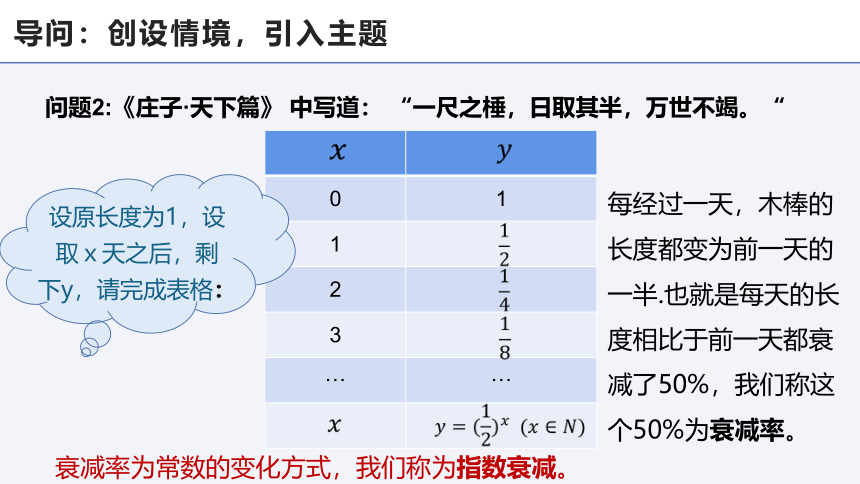
设原长度为1,设取x天之后,剩下y,请完成表格:
衰减率为常数的变化方式,我们称为指数衰减。
问题2:《庄子·天下篇》 中写道: “一尺之棰,日取其半,万世不竭。“
导问:创设情境,引入主题
每经过一天,木棒的长度都变为前一天的一半.也就是每天的长度相比于前一天都衰减了50%,我们称这个50%为衰减率。
以上两个函数在结构上有什么共同点?
结合我们学过的幂函数,能不能将这两个函数的形式用一个统一的格式表示?
深问:步步设疑,激发思考
指数都是自变量,底数都是常数.
【1】 解析式中 的系数为1
【2】 底数 是常数,满足
【3】 自变量 是指数,且
为什么要规定 呢?
、 又会出现什么结果呢?
深问:步步设疑,激发思考
解析式特点:
【定义】
深问:步步设疑,激发思考
【定义】
深问:步步设疑,激发思考
指数函数与我们之前学过的幂函数有什么不同?
指数函数 幂函数
解析式
自变量
指数
底数
区分二者的关键是看自变量x的位置是指数还是底数
【定义】
跟踪训练
深问:步步设疑,激发思考
判断下列函数是不是指数函数:
√
×
×
×
×
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
这两个函数图象有什么关系?
底数互为倒数的两个指数函数的图象关于y轴对称
解问:合作探究,共解问题
探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
在第一象限,图象高低与底数什么关系?
第一象限,底大图高
定点?
恒过定点(0,1)
单调性?
奇偶性?
无
位置?
第一、二象限
定义域?值域?
解问:合作探究,共解问题
探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
你能结合发现的规律,在同一坐标系中做出底数为的
指数函数的大致图象吗?
解问:合作探究,共解问题
图象
定义域、值域 、 定点 单调性
奇偶性 探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
先设出函数的解析式
利用已知条件,求出解析式中的参数
得到函数的解析式
利用解析式,求指数函数的函数值
新问:点拨归纳,提升思维
例1.比较下列各题中两个值的大小:
新问:点拨归纳,提升思维
,
练习1.
新问:点拨归纳,提升思维
新问:点拨归纳,提升思维
新问:点拨归纳,提升思维
这节课我们都学了什么?
指数函数
定义
R
定义域
值域
图
象
性
质
单调性
非奇非偶函数
奇偶性
对称性
过定点(0,1)
在第一象限内“底大图高”
感谢聆听!
第4章 指数函数与对数函数
4.2 指数函数
导问:创设情境,引入主题
给我一个支点,我能够撬动地球。
----阿基米德
给我一张足够大的纸,我能够上月球,你信吗?
给你一张纸,你能折几次呢?
导问:创设情境,引入主题
如果你有一张面积无限、强度无限,厚度为0.01毫米的纸,如果折叠能力无限,那么多次对折,纸张的厚度会变成多少呢?
导问:创设情境,引入主题
问题1:一张薄薄的纸,却折叠出了惊天的气势,蕴含着神奇的数学知识。若把纸张的初始厚度设为1,经过x次对折后, 纸张厚度y与对折次数x之间的关系是什么?
对折次数 纸张厚度
0 1
1
2
3
··· ···
导问:创设情境,引入主题
每折叠一次,得到的纸张的厚度都约为前一次的2倍.也就是每次的厚度相比于折叠之前都增长了100%,我们称这个100%为增长率。
增长率为常数的变化方式,我们称为指数增长。
0 1
1
2
3
··· ···
设原长度为1,设取x天之后,剩下y,请完成表格:
衰减率为常数的变化方式,我们称为指数衰减。
问题2:《庄子·天下篇》 中写道: “一尺之棰,日取其半,万世不竭。“
导问:创设情境,引入主题
每经过一天,木棒的长度都变为前一天的一半.也就是每天的长度相比于前一天都衰减了50%,我们称这个50%为衰减率。
以上两个函数在结构上有什么共同点?
结合我们学过的幂函数,能不能将这两个函数的形式用一个统一的格式表示?
深问:步步设疑,激发思考
指数都是自变量,底数都是常数.
【1】 解析式中 的系数为1
【2】 底数 是常数,满足
【3】 自变量 是指数,且
为什么要规定 呢?
、 又会出现什么结果呢?
深问:步步设疑,激发思考
解析式特点:
【定义】
深问:步步设疑,激发思考
【定义】
深问:步步设疑,激发思考
指数函数与我们之前学过的幂函数有什么不同?
指数函数 幂函数
解析式
自变量
指数
底数
区分二者的关键是看自变量x的位置是指数还是底数
【定义】
跟踪训练
深问:步步设疑,激发思考
判断下列函数是不是指数函数:
√
×
×
×
×
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
-2 4
-1 2
0 1 1
1 2
2 4
解问:合作探究,共解问题
这两个函数图象有什么关系?
底数互为倒数的两个指数函数的图象关于y轴对称
解问:合作探究,共解问题
探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
在第一象限,图象高低与底数什么关系?
第一象限,底大图高
定点?
恒过定点(0,1)
单调性?
奇偶性?
无
位置?
第一、二象限
定义域?值域?
解问:合作探究,共解问题
探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
你能结合发现的规律,在同一坐标系中做出底数为的
指数函数的大致图象吗?
解问:合作探究,共解问题
图象
定义域、值域 、 定点 单调性
奇偶性 探究:请观察指数函数图象随底数的变化情况,并研究指数函数的性质。
先设出函数的解析式
利用已知条件,求出解析式中的参数
得到函数的解析式
利用解析式,求指数函数的函数值
新问:点拨归纳,提升思维
例1.比较下列各题中两个值的大小:
新问:点拨归纳,提升思维
,
练习1.
新问:点拨归纳,提升思维
新问:点拨归纳,提升思维
新问:点拨归纳,提升思维
这节课我们都学了什么?
指数函数
定义
R
定义域
值域
图
象
性
质
单调性
非奇非偶函数
奇偶性
对称性
过定点(0,1)
在第一象限内“底大图高”
感谢聆听!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
