2021-2022学年高一上学期数学 北师大版 必修1 1.3.2 全集与补集 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学 北师大版 必修1 1.3.2 全集与补集 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 16:17:00 | ||
图片预览





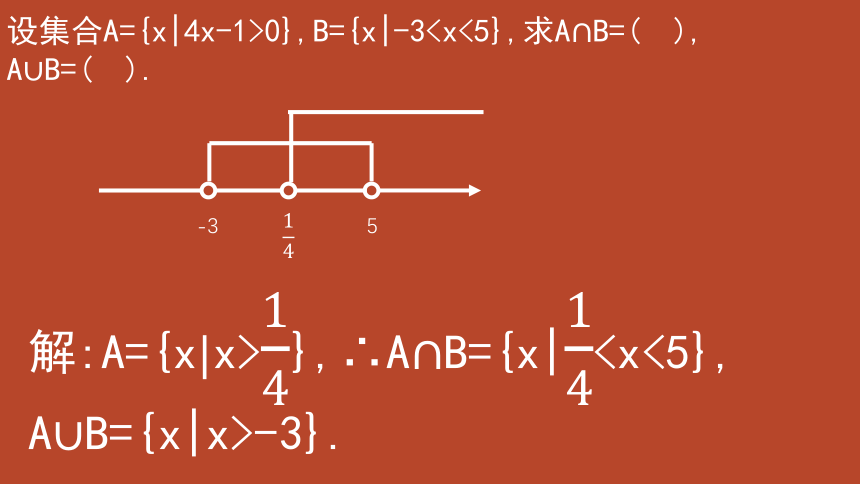


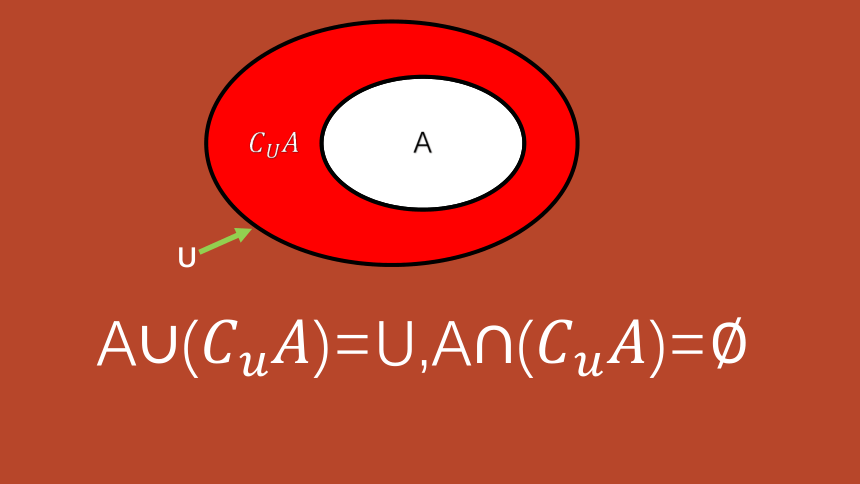
文档简介
(共20张PPT)
3.2全集与补集
教学分析
本节是集合间运算的第二部分,是集合运算的补充,学习完本节,能使集合运算知识系统化,数学方法条理化。集合的交、并、补运算既互相独立,又相互联系,层层深入,使知识体系完备化。
三维目标
理解并掌握全集与补集的定义,会计算简单集合在给定全集中的补集,使学生学会运用数学知识解决实际问题,培养学生分析问题和思考问题的能力,提高学生学习数学的兴趣,
培养其抽象思维能力。
重点难点
教学重点:1.补集的定义。
2.补集的求法及其运算。
教学难点:1.集合运算的系统化
2.补集的混合运算。
教学过程
一、复习旧知
1.交集:
2.并集:
AB={x|xA,且xB},
AB={xxA,或xB}.
AB
B
A
A
B
设集合A={x|4x-1>0},B={x|-3AB=( ).
解:A={xx>},∴AB={x|AB={x|x>-3}.
-3
5
二、推进新课
1.全集的定义:
在研究某些集合的时候,这些集合往往是某个给定集合的子集,这个给定的集合叫作全集.常用符号U表示。
2.补集的定义:
设U是全集,A是U的一个子集(即AU),则由U中所有不属于A的元素组成的集合,叫作U中子集A的补集(或余集),记作,即={x|xU,且A}.
A
U
A()=U,A()=
3.课时例题
例1 试用集合A,B的交集,并集,补集分别表示图中I,II,Ⅲ,IV四个部分所表示的集合.
A Ⅱ
Ⅳ
U
Ⅰ
解:I部分: A∩B;
II部分: A∩(CuB);
Ⅲ部分: B∩(CuA);
IV部分: Cu(A∪B)或(CuB)∩(CuA).
例2 设全集为R,A={x|x<6},
B={x|x>5},求:
(1)A∩B;(2)AUB;
(3)CRA,CRB;
(4)(CRA)∩(CRB);
(5)(CRA)U(CRB);
(6)GR(A∩B
(7)GR(AUB),并指出其中相等的集合.
解:(1)在数轴上,画出集合A和B:
6
5
AB={x|x>5}{x|x<6}={x|5(2)AB={x|x>5}{x|x<6}=R
6
5
(3)在数轴上,画出集合和,
={x|x≤5}, ={x|x≥6}
6
5
(4)CRA(CRB)={x|x≤5}{x|x≥6}=;
(5)(CRA)U(CRB)={x|x≤5}U
{xlx≥6}={x|x≤5,或x≥6}
6
5
(6)CR(AB)={x|x≤5,或:x≥6};
(7)CR(AUB)=.
6
5
补集的性质:
CR(AB)=(CRA)U(CRB);
CR(AUB)=(CRA)∩(CRB)
U
A
B
例3 设全集为R,A={x|x<6},
B={x|x4},则CRA与CRB的
关系是_____.
解析;CRA={x|x≥6},CRB={x|x>4}
4
6
∴CRACRB
课时小结:
全集与补集的概念,符号。
熟练求给定集合的补集
利用好常用数学工具数轴,Venn图解决集合常用问题。
3.2全集与补集
教学分析
本节是集合间运算的第二部分,是集合运算的补充,学习完本节,能使集合运算知识系统化,数学方法条理化。集合的交、并、补运算既互相独立,又相互联系,层层深入,使知识体系完备化。
三维目标
理解并掌握全集与补集的定义,会计算简单集合在给定全集中的补集,使学生学会运用数学知识解决实际问题,培养学生分析问题和思考问题的能力,提高学生学习数学的兴趣,
培养其抽象思维能力。
重点难点
教学重点:1.补集的定义。
2.补集的求法及其运算。
教学难点:1.集合运算的系统化
2.补集的混合运算。
教学过程
一、复习旧知
1.交集:
2.并集:
AB={x|xA,且xB},
AB={xxA,或xB}.
AB
B
A
A
B
设集合A={x|4x-1>0},B={x|-3
解:A={xx>},∴AB={x|
-3
5
二、推进新课
1.全集的定义:
在研究某些集合的时候,这些集合往往是某个给定集合的子集,这个给定的集合叫作全集.常用符号U表示。
2.补集的定义:
设U是全集,A是U的一个子集(即AU),则由U中所有不属于A的元素组成的集合,叫作U中子集A的补集(或余集),记作,即={x|xU,且A}.
A
U
A()=U,A()=
3.课时例题
例1 试用集合A,B的交集,并集,补集分别表示图中I,II,Ⅲ,IV四个部分所表示的集合.
A Ⅱ
Ⅳ
U
Ⅰ
解:I部分: A∩B;
II部分: A∩(CuB);
Ⅲ部分: B∩(CuA);
IV部分: Cu(A∪B)或(CuB)∩(CuA).
例2 设全集为R,A={x|x<6},
B={x|x>5},求:
(1)A∩B;(2)AUB;
(3)CRA,CRB;
(4)(CRA)∩(CRB);
(5)(CRA)U(CRB);
(6)GR(A∩B
(7)GR(AUB),并指出其中相等的集合.
解:(1)在数轴上,画出集合A和B:
6
5
AB={x|x>5}{x|x<6}={x|5
6
5
(3)在数轴上,画出集合和,
={x|x≤5}, ={x|x≥6}
6
5
(4)CRA(CRB)={x|x≤5}{x|x≥6}=;
(5)(CRA)U(CRB)={x|x≤5}U
{xlx≥6}={x|x≤5,或x≥6}
6
5
(6)CR(AB)={x|x≤5,或:x≥6};
(7)CR(AUB)=.
6
5
补集的性质:
CR(AB)=(CRA)U(CRB);
CR(AUB)=(CRA)∩(CRB)
U
A
B
例3 设全集为R,A={x|x<6},
B={x|x4},则CRA与CRB的
关系是_____.
解析;CRA={x|x≥6},CRB={x|x>4}
4
6
∴CRACRB
课时小结:
全集与补集的概念,符号。
熟练求给定集合的补集
利用好常用数学工具数轴,Venn图解决集合常用问题。
