2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测试 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性 同步达标测试 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 22:21:15 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《3.2圆的对称性》同步达标测试(附答案)
一.选择题(共6小题,满分30分)
1.如图,AB是⊙O的直径,∠BOD=120°,点C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为( )
A. B. C. D.
2.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD.若∠BOD=∠BCD,则的度数为( )
A.60° B.90° C.120° D.150°
3.已知⊙O的直径CD为4,弧AC的度数为80°,点B是弧AC的中点,点P在直径CD上移动,则BP+AP的最小值为( )
A.2 B.2 C.2 D.4
4.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
5.如图,扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,则CD的长为( )
A. B.3 C. D.2
6.如图,B为在⊙O的半径OC上一点(不与O,C重合),点E在圆上,以OB,BE为边作矩形OBED,延长DO到点A,使OA=OB,连接AC,则( )
A.AC>DB B.AC<DB C.AC=DB D.AC与BD的大小关系不能确定
二.填空题(共7小题,满分35分)
7.如图,已知四边形ABCD外接圆⊙O的半径为5,对角线AC与BD交于点E,BE=DE,AB=BE,且AC=8,则四边形ABCD的面积为 .
8.如图,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,AC=BD,则弦AC的长为 .
9.点A、C为半径是4的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为 .
10.如图AB、BC为⊙O的弦,AB=,BC=1,∠AOC=90°,则⊙O半径为 .
11.如图,在⊙O中,AB=AC,∠BAC=90°,点P为上任意一点,连接PA,PB,PC,则线段PA,PB,PC之间的数量关系为 .
12.如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 .
13.如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
三.解答题(共8小题,满分55分)
14.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
15.如图,在⊙O中,弦AC⊥BD于点E,连接AB,CD,BC
(1)求证:∠AOB+∠COD=180°;
(2)若AB=8,CD=6,求⊙O的直径.
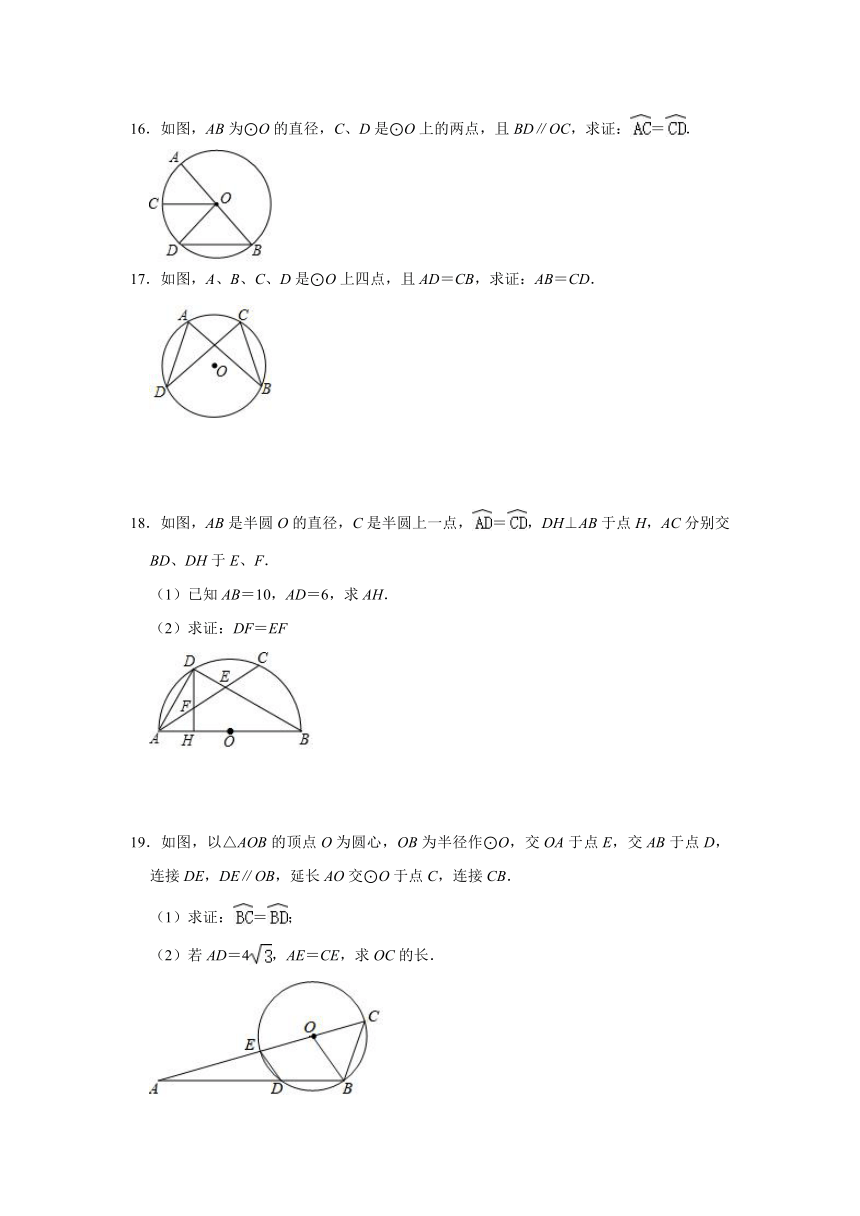
16.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:=.
17.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
18.如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
19.如图,以△AOB的顶点O为圆心,OB为半径作⊙O,交OA于点E,交AB于点D,连接DE,DE∥OB,延长AO交⊙O于点C,连接CB.
(1)求证:=;
(2)若AD=4,AE=CE,求OC的长.
20.如图,在直角△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求弧DE的度数;
(2)若BC=2,AC=6,求BD的长.
21.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
参考答案
一.选择题(共6小题,满分30分)
1.解:连接OC.
∵∠DOB=120°,
∴∠AOD=60°,
∵=,
∴∠DOC=∠BOC=60°,
∴=,
∴OD⊥AC,设OA=r,则OE=r=DE=1,
∴OA=2,
∴AE==,
故选:A.
2.解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴的度数为120°
故选:C.
3.解:过点B关于CD的对称点B′,连接AB′交CD于点P,延长AO交圆O于点E,连接B′E.
∵点B与点B′关于CD对称,
∴PB=PB′..
∴当点B′、P、A在一条直线上时,PB+PA有最小值,最小值为AB′.
∵点B是的中点,
∴=120°.
∴∠B′EA=60°.
∴AB′=AE sin60°=4×=2.
故选:C.
4.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
5.解:连接OC,交AB于F,
∵C是的中点,
∴,
∴∠AOC=∠BOC=∠AOB==60°,OC⊥AB,
Rt△BOF中,OB=OA=6,
∴OF=OB=3,
∴CF=6﹣3=3,
∵CD⊥OA,
∴∠OEC=90°,
∴∠OCE=30°,
∵∠CFD=90°,
∴DF=,CD=2DF=2,
故选:D.
6.解:连接OE.
∵四边形OBED是矩形,
∴OE=BD,
∵△AOC是直角三角形,
∴AC>OC,
∵OE=OC,
∴BD=OC,
∴AC>BD,
故选:A.
二.填空题(共7小题,满分35分)
7.解:∵BE=DE,AB=BE,
∴AB2=2BE2=BE BD,
∴AB:BE=BD:AB,
又∠EBA=∠ABD,
∴△ABE∽△DBA,
∴∠ADB=∠BAE,
∵∠ADB=∠ACB,
∴∠ACB=∠CAB,
∴AB=BC.
连接BO,交AC于H,连接OA,
∵AB=BC,
∴BO⊥AC,
∴CH=AH,
∴CH=AH=AC=4
∵AO=5,
∴OH==3,BH=OB﹣OH=5﹣3=2.
∴S△ABC=AC BH=×8×2=8,
∵E是BD的中点,
∴S△ABE=S△ADE,S△BCE=S△DCE,
∴S△ABC=S△ADC,
∴S四边形ABCD=2S△ABC=16,
故答案为16.
8.解:∵OD⊥AC,
∴=,∠AFO=90°,
又∵AC=BD,
∴=,即+=+,
∴=,
∴==,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=3,
∴AO=BO=,
∴AF=AOsin∠AOF=×=,
则AC=2AF=;
9.解:如图,连接OA,设BD交AC于G,BD交⊙O于F.
∵四边形ABCD是菱形,
∴BD垂直平分线段AC,
∴BF是直径,
∵OD=DF=2,OB=4,
∴BG=DG=3,
∴OG=1,
在Rt△AOG中,AG==,
在Rt△ABG中,AB==2,
如图当点D在OB上时,OD=DB=2,DG=BG=1,
AG==,AD==2,
故答案为2或2.
10.解:作AH⊥CB交CB的延长线于H,连接AC.
由∠AOC=90°,可得∠ABC=135°,
在Rt△AHB中,∵AB=,∠ABH=45°,
∴AH=BH=1,
在Rt△AHC中,∵CH=CB+BH=2,AH=1,
∴AC==,
∵OA=OC,∠AOC=90°,
∴OA=OC=,
故答案为.
11.解:如图作AE⊥PC于E,AF⊥PB交PB的延长线于F.
∵BC是直径,
∴∠BAC=∠EPF=90°,
∵AB=AC,
∴=,
∴∠APF=∠APC,
∵AE⊥PC,AF⊥PF,
∴AE=AF,
∵∠F=∠AEC=90°,
∴Rt△AEC≌Rt△AFB(HL),
∴BF=CE,
∵∠AFP=∠AEP=90°,AP=AP,AF=AE,
∴Rt△APF≌Rt△APE(HL),
∴PF=PE,
∴PB+PC=PF﹣BF+PE+EC=2PE,
∵∠APC=∠ABC=45°,
∴△APE是等腰直角三角形,
∴PA=PE,
∴PE=PA,
∴PB+PC=PA.
故答案为PB+PC=PA.
12.解:∵,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=84°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣84°)=48°.
故答案为:48°
13.解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,从条件上看,AB=CD,推不出OB⊥CD这样的位置关系,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
三.解答题(共8小题,满分55分)
14.证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
∴CD=BF,
在△BFG和△CDG中,
∵,
∴△BFG≌△CDG(AAS);
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
15.(1)证明:延长BO交⊙O 于F,连接DF,AD.
∵BF是直径,
∴∠BDF=90°,
∴DF⊥BD,
∵AC⊥BD,
∴AC∥DF,
∴∠CAD=∠ADF,
∴=,
∴∠COD=∠AOF,
∵∠AOB+∠AOF=180°,
∴∠AOB+∠COD=180°.
(2)解:连接AF.
由(1)可知:=,
∴AF=CD=6,
∵BF是直径,
∴∠BAF=90°,
∴BF===10,
∴⊙O的直径为10.
16.证明:∵OB=OD,
∴∠D=∠B,
∵BD∥OC,
∴∠D=∠COD,∠AOC=∠B,
∴∠AOC=∠COD,
∴=.
17.证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
18.(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵DH⊥AB,
∴∠DHA=∠ADB=90°,
又∵∠DAB=∠HAD,
∴△DAB∽△HAD,
∴=即=,
∴AH=3.6.
(2)证明:∵=,
∴∠DAC=∠DBA,
∵DH⊥AB,
∴∠FDE+∠B=90°,
∵∠ADB=90°,
∴∠DEF+∠DAC=90°,
∴∠DEF=∠FDE,
∴DF=EF.
19.(1)证明:如图1,连接CD交OB于F,
∵CE是直径,
∴∠EDC=90°,
∵DE∥OB,
∴∠EDC=∠OFC=90°,
即OB⊥CD,
∴;
(2)解:如图2,连接CD交OB于F,连接EF,
由(1)得:DE∥OB,OB⊥CD,点F是CD的中点,
∵AE=CE,
∴EF∥AD,EF=AD=2,
∵O是CE的中点,F是CD的中点,
∴OF=DE,
∵EF∥BD,DE∥BF,
∴四边形EFBD是平行四边形,
∴BF=DE,
设OF=x,则BF=DE=2x,OC=OB=3x,
∵,
∴BC=BD=EF=2,
∵DF2=CF2
∴,
解得:x=±1,
∵x>0,
∴x=1,
∴OC=3x=3.
20.解:(1)连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴∠DCE=40°
∴的度数为40°;
(2)延长AC交⊙C与点F,
∵∠BCA=90°,BC=2,AC=6,
∴AB===2,AE=6﹣2=4.
∵AB与AF均是⊙C的割线,
∴AD AB=AE AF,即2 AD=4×8,解得AD=,
∴BD=AB﹣AD=2﹣=.
解法二:作CH⊥AB于H,利用面积法求出CH,再利用勾股定理求出BH,由BD=2BH即可解决问题.
21.解:连接CD,如图,
∵∠C=90°,∠B=28°,
∴∠A=90°﹣28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°﹣2×62°=56°
∴的度数为56°;
∵∠DCE=90°﹣∠ACD=34°,
∴的度数为34°.
一.选择题(共6小题,满分30分)
1.如图,AB是⊙O的直径,∠BOD=120°,点C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为( )
A. B. C. D.
2.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连接OB,OD.若∠BOD=∠BCD,则的度数为( )
A.60° B.90° C.120° D.150°
3.已知⊙O的直径CD为4,弧AC的度数为80°,点B是弧AC的中点,点P在直径CD上移动,则BP+AP的最小值为( )
A.2 B.2 C.2 D.4
4.在圆中,与半径相等的弦所对的圆心角的度数为( )
A.30° B.45° C.60° D.90°
5.如图,扇形OAB中,∠AOB=120°,半径OA=6,C是弧AB的中点,CD⊥OA,交AB于点D,则CD的长为( )
A. B.3 C. D.2
6.如图,B为在⊙O的半径OC上一点(不与O,C重合),点E在圆上,以OB,BE为边作矩形OBED,延长DO到点A,使OA=OB,连接AC,则( )
A.AC>DB B.AC<DB C.AC=DB D.AC与BD的大小关系不能确定
二.填空题(共7小题,满分35分)
7.如图,已知四边形ABCD外接圆⊙O的半径为5,对角线AC与BD交于点E,BE=DE,AB=BE,且AC=8,则四边形ABCD的面积为 .
8.如图,已知半⊙O的直径AB为3,弦AC与弦BD交于点E,OD⊥AC,垂足为点F,AC=BD,则弦AC的长为 .
9.点A、C为半径是4的圆周上两点,点B为弧AC的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为 .
10.如图AB、BC为⊙O的弦,AB=,BC=1,∠AOC=90°,则⊙O半径为 .
11.如图,在⊙O中,AB=AC,∠BAC=90°,点P为上任意一点,连接PA,PB,PC,则线段PA,PB,PC之间的数量关系为 .
12.如图,AB是⊙O的直径,==,∠COD=32°,则∠AEO的度数 .
13.如图,⊙O的动弦AB,CD相交于点E,且AB=CD,∠BED=α(0°<α<90°).在①∠BOD=α,②∠OAB=90°﹣α,③∠ABC=α中,一定成立的是 (填序号).
三.解答题(共8小题,满分55分)
14.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:△BFG≌△CDG;
(2)若AD=BE=2,求BF的长.
15.如图,在⊙O中,弦AC⊥BD于点E,连接AB,CD,BC
(1)求证:∠AOB+∠COD=180°;
(2)若AB=8,CD=6,求⊙O的直径.
16.如图,AB为⊙O的直径,C、D是⊙O上的两点,且BD∥OC,求证:=.
17.如图,A、B、C、D是⊙O上四点,且AD=CB,求证:AB=CD.
18.如图,AB是半圆O的直径,C是半圆上一点,=,DH⊥AB于点H,AC分别交BD、DH于E、F.
(1)已知AB=10,AD=6,求AH.
(2)求证:DF=EF
19.如图,以△AOB的顶点O为圆心,OB为半径作⊙O,交OA于点E,交AB于点D,连接DE,DE∥OB,延长AO交⊙O于点C,连接CB.
(1)求证:=;
(2)若AD=4,AE=CE,求OC的长.
20.如图,在直角△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求弧DE的度数;
(2)若BC=2,AC=6,求BD的长.
21.如图,在△ABC中,∠C=90°,∠B=28°,以C为圆心,CA为半径的圆交AB于点D,交BC于点E.求、的度数.
参考答案
一.选择题(共6小题,满分30分)
1.解:连接OC.
∵∠DOB=120°,
∴∠AOD=60°,
∵=,
∴∠DOC=∠BOC=60°,
∴=,
∴OD⊥AC,设OA=r,则OE=r=DE=1,
∴OA=2,
∴AE==,
故选:A.
2.解:∵四边形ABCD内接于⊙O,
∴∠BCD+∠A=180°,
∵∠BOD=2∠A,∠BOD=∠BCD,
∴2∠A+∠A=180°,
解得:∠A=60°,
∴∠BOD=120°,
∴的度数为120°
故选:C.
3.解:过点B关于CD的对称点B′,连接AB′交CD于点P,延长AO交圆O于点E,连接B′E.
∵点B与点B′关于CD对称,
∴PB=PB′..
∴当点B′、P、A在一条直线上时,PB+PA有最小值,最小值为AB′.
∵点B是的中点,
∴=120°.
∴∠B′EA=60°.
∴AB′=AE sin60°=4×=2.
故选:C.
4.解:如图,
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠AOB=60°.
故选:C.
5.解:连接OC,交AB于F,
∵C是的中点,
∴,
∴∠AOC=∠BOC=∠AOB==60°,OC⊥AB,
Rt△BOF中,OB=OA=6,
∴OF=OB=3,
∴CF=6﹣3=3,
∵CD⊥OA,
∴∠OEC=90°,
∴∠OCE=30°,
∵∠CFD=90°,
∴DF=,CD=2DF=2,
故选:D.
6.解:连接OE.
∵四边形OBED是矩形,
∴OE=BD,
∵△AOC是直角三角形,
∴AC>OC,
∵OE=OC,
∴BD=OC,
∴AC>BD,
故选:A.
二.填空题(共7小题,满分35分)
7.解:∵BE=DE,AB=BE,
∴AB2=2BE2=BE BD,
∴AB:BE=BD:AB,
又∠EBA=∠ABD,
∴△ABE∽△DBA,
∴∠ADB=∠BAE,
∵∠ADB=∠ACB,
∴∠ACB=∠CAB,
∴AB=BC.
连接BO,交AC于H,连接OA,
∵AB=BC,
∴BO⊥AC,
∴CH=AH,
∴CH=AH=AC=4
∵AO=5,
∴OH==3,BH=OB﹣OH=5﹣3=2.
∴S△ABC=AC BH=×8×2=8,
∵E是BD的中点,
∴S△ABE=S△ADE,S△BCE=S△DCE,
∴S△ABC=S△ADC,
∴S四边形ABCD=2S△ABC=16,
故答案为16.
8.解:∵OD⊥AC,
∴=,∠AFO=90°,
又∵AC=BD,
∴=,即+=+,
∴=,
∴==,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=3,
∴AO=BO=,
∴AF=AOsin∠AOF=×=,
则AC=2AF=;
9.解:如图,连接OA,设BD交AC于G,BD交⊙O于F.
∵四边形ABCD是菱形,
∴BD垂直平分线段AC,
∴BF是直径,
∵OD=DF=2,OB=4,
∴BG=DG=3,
∴OG=1,
在Rt△AOG中,AG==,
在Rt△ABG中,AB==2,
如图当点D在OB上时,OD=DB=2,DG=BG=1,
AG==,AD==2,
故答案为2或2.
10.解:作AH⊥CB交CB的延长线于H,连接AC.
由∠AOC=90°,可得∠ABC=135°,
在Rt△AHB中,∵AB=,∠ABH=45°,
∴AH=BH=1,
在Rt△AHC中,∵CH=CB+BH=2,AH=1,
∴AC==,
∵OA=OC,∠AOC=90°,
∴OA=OC=,
故答案为.
11.解:如图作AE⊥PC于E,AF⊥PB交PB的延长线于F.
∵BC是直径,
∴∠BAC=∠EPF=90°,
∵AB=AC,
∴=,
∴∠APF=∠APC,
∵AE⊥PC,AF⊥PF,
∴AE=AF,
∵∠F=∠AEC=90°,
∴Rt△AEC≌Rt△AFB(HL),
∴BF=CE,
∵∠AFP=∠AEP=90°,AP=AP,AF=AE,
∴Rt△APF≌Rt△APE(HL),
∴PF=PE,
∴PB+PC=PF﹣BF+PE+EC=2PE,
∵∠APC=∠ABC=45°,
∴△APE是等腰直角三角形,
∴PA=PE,
∴PE=PA,
∴PB+PC=PA.
故答案为PB+PC=PA.
12.解:∵,∠COD=32°,
∴∠BOC=∠EOD=∠COD=32°,
∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=84°.
又∵OA=OE,
∴∠AEO=∠OAE,
∴∠AEO=×(180°﹣84°)=48°.
故答案为:48°
13.解:如图,连接OC,设OB交CD于K.
∵AB=CD,OD=OC=OB=OA,
∴△AOB≌△COD(SSS),
∴∠CDO=∠OBA,
∵∠DKO=∠BKE,
∴∠DOK=∠BEK=α,
即∠BOD=α,故①正确,
不妨设,∠OAB=90°﹣α,
∵OA=OB,
∴∠OAB=∠OBA,
∴∠OBE+∠BEK=90°,
∴∠BKE=90°,
∴OB⊥CD,从条件上看,AB=CD,推不出OB⊥CD这样的位置关系,故②错误,
∵CD=AB,
∴=,
∴=,
∴∠ABC=∠DOB=α,故③正确.
故答案为①③.
三.解答题(共8小题,满分55分)
14.证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
∴CD=BF,
在△BFG和△CDG中,
∵,
∴△BFG≌△CDG(AAS);
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
15.(1)证明:延长BO交⊙O 于F,连接DF,AD.
∵BF是直径,
∴∠BDF=90°,
∴DF⊥BD,
∵AC⊥BD,
∴AC∥DF,
∴∠CAD=∠ADF,
∴=,
∴∠COD=∠AOF,
∵∠AOB+∠AOF=180°,
∴∠AOB+∠COD=180°.
(2)解:连接AF.
由(1)可知:=,
∴AF=CD=6,
∵BF是直径,
∴∠BAF=90°,
∴BF===10,
∴⊙O的直径为10.
16.证明:∵OB=OD,
∴∠D=∠B,
∵BD∥OC,
∴∠D=∠COD,∠AOC=∠B,
∴∠AOC=∠COD,
∴=.
17.证明:∵AD=CB,
∴=,
∴+=+,
即=,
∴AB=CD.
18.(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵DH⊥AB,
∴∠DHA=∠ADB=90°,
又∵∠DAB=∠HAD,
∴△DAB∽△HAD,
∴=即=,
∴AH=3.6.
(2)证明:∵=,
∴∠DAC=∠DBA,
∵DH⊥AB,
∴∠FDE+∠B=90°,
∵∠ADB=90°,
∴∠DEF+∠DAC=90°,
∴∠DEF=∠FDE,
∴DF=EF.
19.(1)证明:如图1,连接CD交OB于F,
∵CE是直径,
∴∠EDC=90°,
∵DE∥OB,
∴∠EDC=∠OFC=90°,
即OB⊥CD,
∴;
(2)解:如图2,连接CD交OB于F,连接EF,
由(1)得:DE∥OB,OB⊥CD,点F是CD的中点,
∵AE=CE,
∴EF∥AD,EF=AD=2,
∵O是CE的中点,F是CD的中点,
∴OF=DE,
∵EF∥BD,DE∥BF,
∴四边形EFBD是平行四边形,
∴BF=DE,
设OF=x,则BF=DE=2x,OC=OB=3x,
∵,
∴BC=BD=EF=2,
∵DF2=CF2
∴,
解得:x=±1,
∵x>0,
∴x=1,
∴OC=3x=3.
20.解:(1)连接CD,
∵∠A=25°,
∴∠B=65°,
∵CB=CD,
∴∠B=∠CDB=65°,
∴∠BCD=50°,
∴∠DCE=40°
∴的度数为40°;
(2)延长AC交⊙C与点F,
∵∠BCA=90°,BC=2,AC=6,
∴AB===2,AE=6﹣2=4.
∵AB与AF均是⊙C的割线,
∴AD AB=AE AF,即2 AD=4×8,解得AD=,
∴BD=AB﹣AD=2﹣=.
解法二:作CH⊥AB于H,利用面积法求出CH,再利用勾股定理求出BH,由BD=2BH即可解决问题.
21.解:连接CD,如图,
∵∠C=90°,∠B=28°,
∴∠A=90°﹣28°=62°,
∵CA=CD,
∴∠A=∠ADC=62°,
∴∠ACD=180°﹣2×62°=56°
∴的度数为56°;
∵∠DCE=90°﹣∠ACD=34°,
∴的度数为34°.
