2021-2022学年苏科版八年级数学上册第5章平面直角坐标系 单元综合练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册第5章平面直角坐标系 单元综合练习题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 263.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 22:23:31 | ||
图片预览



文档简介
2021-2022学年苏科版八年级数学上册《第5章平面直角坐标系》单元综合练习题(附答案)
1.在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)
2.如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为( )
A.3 B.4 C.4.6 D.2
3.如图,直角坐标系中两点A(0,4),B(1,0),P为线段AB上一动点,作点B关于射线OP的对称点C,则线段AC的最小值为( )
A.3 B.4 C. D.
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
5.若点A(﹣4,m﹣3),B(2n,1)关于x轴对称,则( )
A.m=2,n=0 B.m=2,n=﹣2 C.m=4,n=2 D.m=4,n=﹣2
6.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
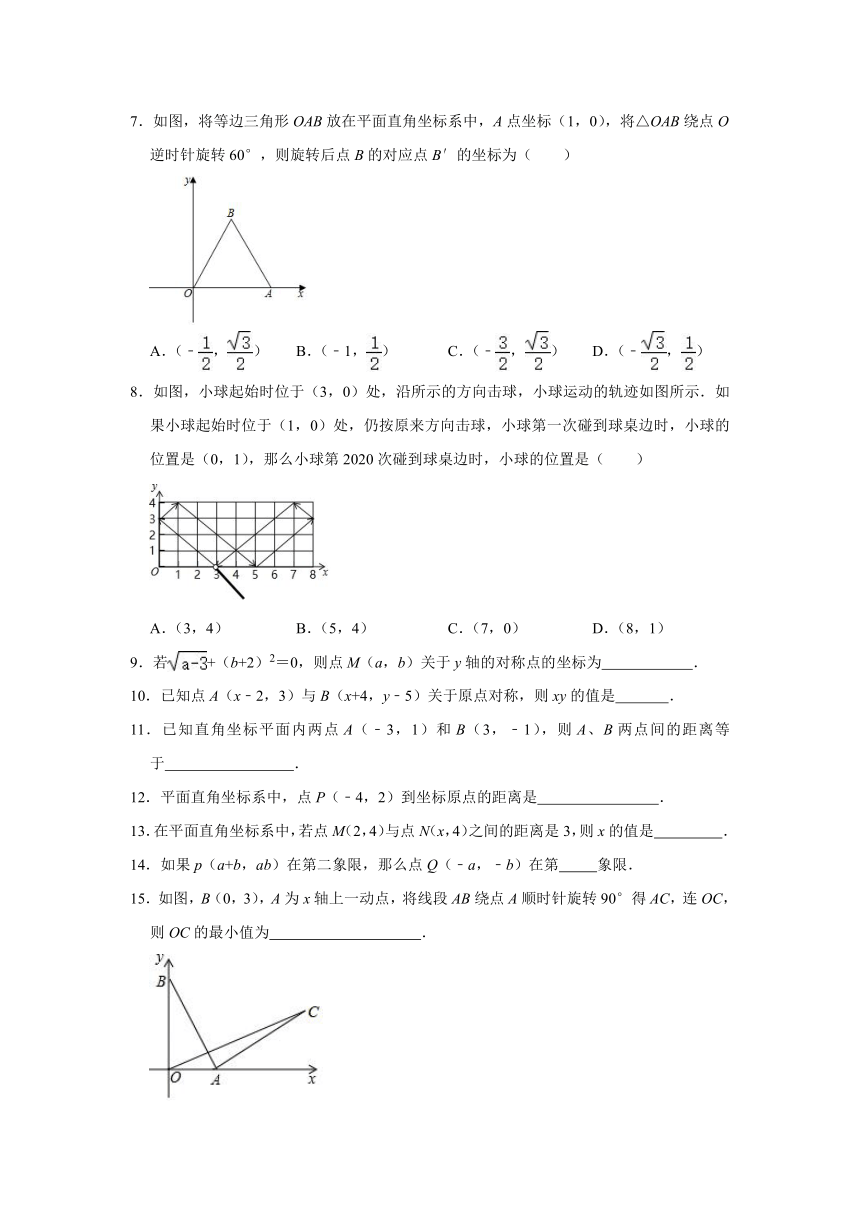
7.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,) B.(﹣1,) C.(﹣,) D.(﹣,)
8.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4) B.(5,4) C.(7,0) D.(8,1)
9.若+(b+2)2=0,则点M(a,b)关于y轴的对称点的坐标为 .
10.已知点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,则xy的值是 .
11.已知直角坐标平面内两点A(﹣3,1)和B(3,﹣1),则A、B两点间的距离等于 .
12.平面直角坐标系中,点P(﹣4,2)到坐标原点的距离是 .
13.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
14.如果p(a+b,ab)在第二象限,那么点Q(﹣a,﹣b)在第 象限.
15.如图,B(0,3),A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连OC,则OC的最小值为 .
16.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD BC= .
17.如图,点A、B分别在y轴和x轴正半轴上滑动,且保持线段AB=4,点D坐标为(4,3),点A关于点D的对称点为点C,连接BC,则BC的最小值为 .
18.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P与x轴的距离为9,求m的值;
(2)若点P在过点A(2,﹣3)且与y轴平行的直线上,求点P的坐标.
19.已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
20.如图在平面直角坐标系xOy中,A(6,0),B(6,6),将Rt△OAB绕点O逆时针旋转120°后得到Rt△OA1B1
(1)填空:∠A1OB= ;
(2)求A1的坐标;
(3)求B1的坐标.
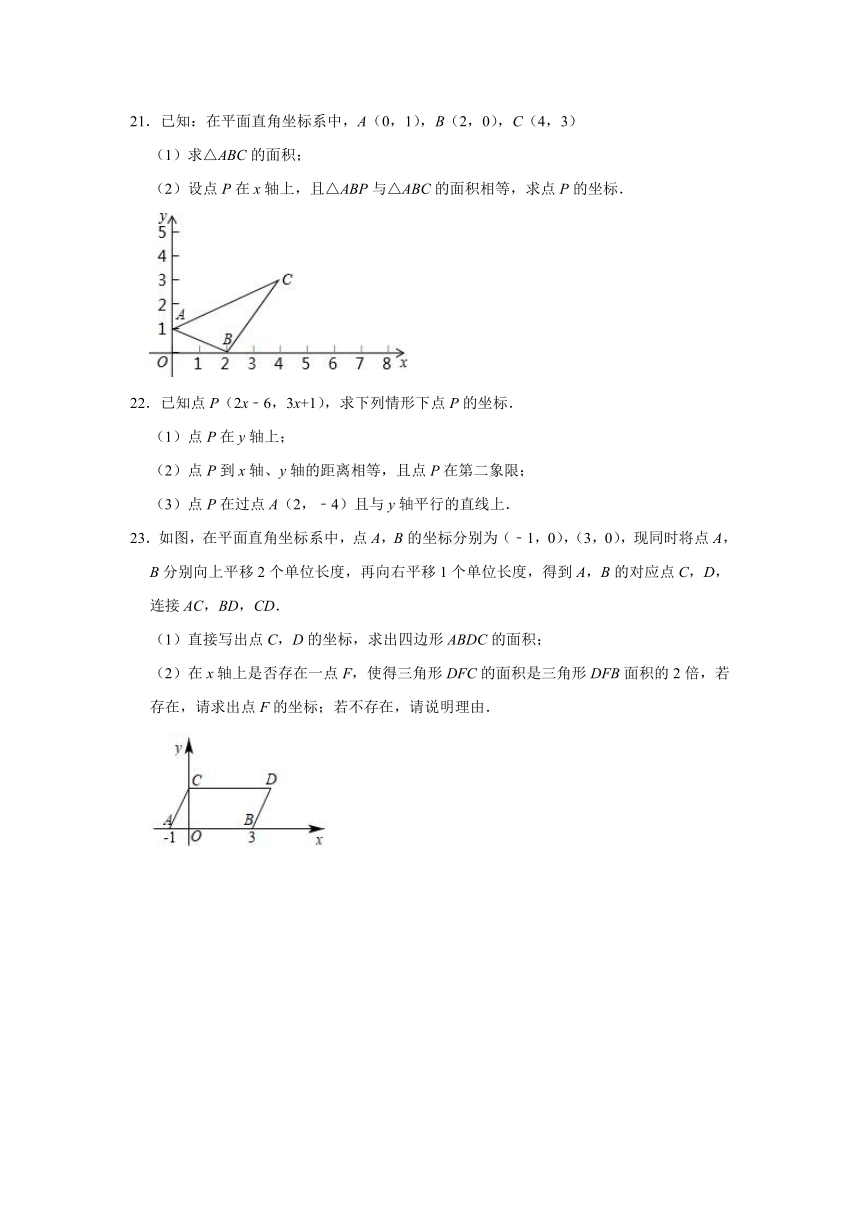
21.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
22.已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
23.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案
1.解:依题意可得:
∵AC∥x轴,A(﹣3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即
BC的最小值=5﹣2=3,
此时点C的坐标为(3,2),
故选:D.
2.解:设点P(x,0),
根据题意得,x2+22=(5﹣x)2+52,
解得:x=4.6,
∴OP=4.6,
故选:C.
3.解:连接OC、AC,
∵A(0,4),B(1,0),
∴OA=4,OB=1,
∵C是点B关于射线OP的对称点,
∴OC=OB=1,
∵AC≥OA﹣OC,
∴AC≥4﹣1=3,
∴AC的最小值为3,
故选:A.
4.解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE==,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
5.解:根据题意:
m﹣3=﹣1,2n=﹣4,
所以m=2,n=﹣2.
故选:B.
6.解:∵AB∥x轴,
∴b=5,a≠﹣1,
故选:C.
7.解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
8.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
9.解:∵+(b+2)2=0,
∴a=3,b=﹣2;
∴点M(a,b)关于y轴的对称点的坐标为(﹣3,﹣2).
10.解:∵点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,
∴x﹣2+x+4=0,3+y﹣5=0,
解得:x=﹣1,y=2,
则xy的值是:﹣2.
故答案为:﹣2.
11.解:∵直角坐标平面内两点 A(﹣3,1)和B(3,﹣1),
∴A、B两点间的距离等于=2,
故答案为2.
12.解:由题意可知:P(﹣4,2)到坐标原点的距离:=2
故答案为:2
13.解:∵点M(2,4)与点N(x,4)之间的距离是3,
∴|2﹣x|=3,
解得,x=﹣1或x=5,
故答案为:﹣1或5.
14.解:由题意,得
a+b<0,ab>0,
得a<0,b<0,
﹣a>0,﹣b>0,
点Q (﹣a,﹣b) 在第一象限,
故答案为:一.
15.解:如图,在x轴的正半轴上取一点H,使得OH=OB=3,在OB上取一点D,使得OD=OA.
∵OB=OH,OD=OA,
∴BD=AH,
∵∠HAC+∠OAB=90°,∠OAB+∠ABO=90°,
∴∠HAC=∠DBA,
∵BA=AC,
∵△BDA≌△AHC(SAS),
∴∠AHC=∠ADB,
∵OD=OA,∠AOD=90°,
∴∠ADO=45°,
∴∠AHC=∠ADB=135°,
∵H(3,0),
∴直线CH的解析式为y=x﹣3,
∴点C在直线y=x﹣3上运动,作OP⊥CH于P,易知OP=,
∴OC 的最小值=OP=,
故答案为.
16.解:过B作BE⊥x轴于E,过C作CF⊥y轴于F,
∵B(m,3),
∴BE=3,
∵A(4,0),
∴AO=4,
∵C(n,﹣5),
∴OF=5,
∵S△AOB=AO BE=×4×3=6,
S△AOC=AO OF=×4×5=10,
∴S△AOB+S△AOC=6+10=16,
∵S△ABC=S△AOB+S△AOC,
∴BC AD=16,
∴BC AD=32,
故答案为:32.
17.解:如图所示,取AB的中点E,连接OE,DE,OD,
由题可得,D是AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵点D坐标为(4,3),
∴OD==5,
∵Rt△ABO中,OE=AB=×4=2,
∴当O,E,D在同一直线上时,DE的最小值等于OD﹣OE=3,
∴BC的最小值等于6,
故答案为:6.
18.解:(1)因为点P(2﹣m,3m+6),点P在x轴的距离为9,
所以|3m+6|=9,
解得m=1或﹣5.
答:m的值为1或﹣5;
(2)因为点P在过点A(2,﹣3)且与y轴平行的直线上,
所以2﹣m=2,
解得m=0,
所以3m+6=6,
所以点P的坐标为(2,6).
19.解:(1)∵点M在x轴上,
∴a﹣1=0,
∴a=1,
3a﹣8=3﹣8=﹣5,a﹣1=0,
∴点M的坐标是(﹣5,0);
(2)∵点M在第二、四象限的角平分线上,
∴3a﹣8+a﹣1=0,
解得a=,
∴a﹣1=﹣1=,
∴点M的坐标为(﹣,);
(3)∵直线MN∥y轴,
∴3a﹣8=1,
解得a=3,
∴a﹣1=3﹣1=2,
点M(1,2).
20.解:(1)∵A(6,0),B(6,6),
∴△AOB是等腰直角三角形,
∴∠AOB=45°,
∵∠AOA1=120°,
∴∠A1OB=75°,
故答案为75°.
(2)作A1H⊥y轴于H.
∵OA1=6,∠A1OH=30°,
∴A1H=OA1=3,OH=A1H=3,
∴A1(﹣3,3).
(3)作B1K⊥OH于K,在B1K上取一点J,使得OJ=JB1,连接OJ.
由题意OB1=OB=6,设OK=m,则OJ=JB=2m,JK=m,
∵OK2+B1K2=B1O2,
∴m2+(2m+m)2=72,
解得m=3﹣3(负根已经舍弃),
∴KB1=3+3,
∴B1(﹣3﹣3,3﹣3).
21.解:(1)过点C作CD⊥x轴,CE⊥y,垂足分别为D、E.
S△ABC=S四边形CDEO﹣S△AEC﹣S△ABO﹣S△BCD
=3×4﹣×2×4﹣×1×2﹣×2×3
=12﹣4﹣1﹣3
=4.
(2)设点P的坐标为(x,0),则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4.
解得:x=10或x=﹣6.
所以点P的坐标为(10,0)或(﹣6,0).
22.解:(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
23.解:(1)C(0,2),D(4,2)
S四边形ABDC=AB OC=4×2=8;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
1.在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,5) B.10,(3,﹣5) C.1,(3,4) D.3,(3,2)
2.如图,在平面直角坐标系中,点P为x轴上一点,且到A(0,2)和点B(5,5)的距离相等,则线段OP的长度为( )
A.3 B.4 C.4.6 D.2
3.如图,直角坐标系中两点A(0,4),B(1,0),P为线段AB上一动点,作点B关于射线OP的对称点C,则线段AC的最小值为( )
A.3 B.4 C. D.
4.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,) B.(,﹣1) C.(﹣,1) D.(﹣2,1)
5.若点A(﹣4,m﹣3),B(2n,1)关于x轴对称,则( )
A.m=2,n=0 B.m=2,n=﹣2 C.m=4,n=2 D.m=4,n=﹣2
6.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
7.如图,将等边三角形OAB放在平面直角坐标系中,A点坐标(1,0),将△OAB绕点O逆时针旋转60°,则旋转后点B的对应点B′的坐标为( )
A.(﹣,) B.(﹣1,) C.(﹣,) D.(﹣,)
8.如图,小球起始时位于(3,0)处,沿所示的方向击球,小球运动的轨迹如图所示.如果小球起始时位于(1,0)处,仍按原来方向击球,小球第一次碰到球桌边时,小球的位置是(0,1),那么小球第2020次碰到球桌边时,小球的位置是( )
A.(3,4) B.(5,4) C.(7,0) D.(8,1)
9.若+(b+2)2=0,则点M(a,b)关于y轴的对称点的坐标为 .
10.已知点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,则xy的值是 .
11.已知直角坐标平面内两点A(﹣3,1)和B(3,﹣1),则A、B两点间的距离等于 .
12.平面直角坐标系中,点P(﹣4,2)到坐标原点的距离是 .
13.在平面直角坐标系中,若点M(2,4)与点N(x,4)之间的距离是3,则x的值是 .
14.如果p(a+b,ab)在第二象限,那么点Q(﹣a,﹣b)在第 象限.
15.如图,B(0,3),A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连OC,则OC的最小值为 .
16.如图所示,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若B(m,3),C(n,﹣5),A(4,0),则AD BC= .
17.如图,点A、B分别在y轴和x轴正半轴上滑动,且保持线段AB=4,点D坐标为(4,3),点A关于点D的对称点为点C,连接BC,则BC的最小值为 .
18.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P与x轴的距离为9,求m的值;
(2)若点P在过点A(2,﹣3)且与y轴平行的直线上,求点P的坐标.
19.已知点M(3a﹣8,a﹣1),分别根据下列条件求出点M的坐标.
(1)点M在x轴上;
(2)点M在第二、四象限的角平分线上;
(3)点N坐标为(1,6),并且直线MN∥y轴.
20.如图在平面直角坐标系xOy中,A(6,0),B(6,6),将Rt△OAB绕点O逆时针旋转120°后得到Rt△OA1B1
(1)填空:∠A1OB= ;
(2)求A1的坐标;
(3)求B1的坐标.
21.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
22.已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
23.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.
参考答案
1.解:依题意可得:
∵AC∥x轴,A(﹣3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即
BC的最小值=5﹣2=3,
此时点C的坐标为(3,2),
故选:D.
2.解:设点P(x,0),
根据题意得,x2+22=(5﹣x)2+52,
解得:x=4.6,
∴OP=4.6,
故选:C.
3.解:连接OC、AC,
∵A(0,4),B(1,0),
∴OA=4,OB=1,
∵C是点B关于射线OP的对称点,
∴OC=OB=1,
∵AC≥OA﹣OC,
∴AC≥4﹣1=3,
∴AC的最小值为3,
故选:A.
4.解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE==,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
5.解:根据题意:
m﹣3=﹣1,2n=﹣4,
所以m=2,n=﹣2.
故选:B.
6.解:∵AB∥x轴,
∴b=5,a≠﹣1,
故选:C.
7.解:如图,故点B作BH⊥OA于H,设BB′交y轴于J.
∵A(1,0),
∴OA=1,
∵△AOB是等边三角形,BH⊥OA,
∴OH=AH=OA=,BH=OH=,
∴B(,),
∵∠AOB=∠BOB′=60°,∠JOA=90°,
∴∠BOJ=∠JOB′=30°,
∵OB=OB′,
∴BB′⊥OJ,
∴BJ=JB′,
∴B,B′关于y轴对称,
∴B′(﹣,),
故选:A.
8.解:由图可得,
点(1,0)第一次碰撞后的点的坐标为(0,1),
第二次碰撞后的点的坐标为(3,4),
第三次碰撞后的点的坐标为(7,0),
第四次碰撞后的点的坐标为(8,1),
第五次碰撞后的点的坐标为(5,4),
第六次碰撞后的点的坐标为(1,0),
…,
∵2020÷6=336…4,
∴小球第2020次碰到球桌边时,小球的位置是(8,1),
故选:D.
9.解:∵+(b+2)2=0,
∴a=3,b=﹣2;
∴点M(a,b)关于y轴的对称点的坐标为(﹣3,﹣2).
10.解:∵点A(x﹣2,3)与B(x+4,y﹣5)关于原点对称,
∴x﹣2+x+4=0,3+y﹣5=0,
解得:x=﹣1,y=2,
则xy的值是:﹣2.
故答案为:﹣2.
11.解:∵直角坐标平面内两点 A(﹣3,1)和B(3,﹣1),
∴A、B两点间的距离等于=2,
故答案为2.
12.解:由题意可知:P(﹣4,2)到坐标原点的距离:=2
故答案为:2
13.解:∵点M(2,4)与点N(x,4)之间的距离是3,
∴|2﹣x|=3,
解得,x=﹣1或x=5,
故答案为:﹣1或5.
14.解:由题意,得
a+b<0,ab>0,
得a<0,b<0,
﹣a>0,﹣b>0,
点Q (﹣a,﹣b) 在第一象限,
故答案为:一.
15.解:如图,在x轴的正半轴上取一点H,使得OH=OB=3,在OB上取一点D,使得OD=OA.
∵OB=OH,OD=OA,
∴BD=AH,
∵∠HAC+∠OAB=90°,∠OAB+∠ABO=90°,
∴∠HAC=∠DBA,
∵BA=AC,
∵△BDA≌△AHC(SAS),
∴∠AHC=∠ADB,
∵OD=OA,∠AOD=90°,
∴∠ADO=45°,
∴∠AHC=∠ADB=135°,
∵H(3,0),
∴直线CH的解析式为y=x﹣3,
∴点C在直线y=x﹣3上运动,作OP⊥CH于P,易知OP=,
∴OC 的最小值=OP=,
故答案为.
16.解:过B作BE⊥x轴于E,过C作CF⊥y轴于F,
∵B(m,3),
∴BE=3,
∵A(4,0),
∴AO=4,
∵C(n,﹣5),
∴OF=5,
∵S△AOB=AO BE=×4×3=6,
S△AOC=AO OF=×4×5=10,
∴S△AOB+S△AOC=6+10=16,
∵S△ABC=S△AOB+S△AOC,
∴BC AD=16,
∴BC AD=32,
故答案为:32.
17.解:如图所示,取AB的中点E,连接OE,DE,OD,
由题可得,D是AC的中点,
∴DE是△ABC的中位线,
∴BC=2DE,
∵点D坐标为(4,3),
∴OD==5,
∵Rt△ABO中,OE=AB=×4=2,
∴当O,E,D在同一直线上时,DE的最小值等于OD﹣OE=3,
∴BC的最小值等于6,
故答案为:6.
18.解:(1)因为点P(2﹣m,3m+6),点P在x轴的距离为9,
所以|3m+6|=9,
解得m=1或﹣5.
答:m的值为1或﹣5;
(2)因为点P在过点A(2,﹣3)且与y轴平行的直线上,
所以2﹣m=2,
解得m=0,
所以3m+6=6,
所以点P的坐标为(2,6).
19.解:(1)∵点M在x轴上,
∴a﹣1=0,
∴a=1,
3a﹣8=3﹣8=﹣5,a﹣1=0,
∴点M的坐标是(﹣5,0);
(2)∵点M在第二、四象限的角平分线上,
∴3a﹣8+a﹣1=0,
解得a=,
∴a﹣1=﹣1=,
∴点M的坐标为(﹣,);
(3)∵直线MN∥y轴,
∴3a﹣8=1,
解得a=3,
∴a﹣1=3﹣1=2,
点M(1,2).
20.解:(1)∵A(6,0),B(6,6),
∴△AOB是等腰直角三角形,
∴∠AOB=45°,
∵∠AOA1=120°,
∴∠A1OB=75°,
故答案为75°.
(2)作A1H⊥y轴于H.
∵OA1=6,∠A1OH=30°,
∴A1H=OA1=3,OH=A1H=3,
∴A1(﹣3,3).
(3)作B1K⊥OH于K,在B1K上取一点J,使得OJ=JB1,连接OJ.
由题意OB1=OB=6,设OK=m,则OJ=JB=2m,JK=m,
∵OK2+B1K2=B1O2,
∴m2+(2m+m)2=72,
解得m=3﹣3(负根已经舍弃),
∴KB1=3+3,
∴B1(﹣3﹣3,3﹣3).
21.解:(1)过点C作CD⊥x轴,CE⊥y,垂足分别为D、E.
S△ABC=S四边形CDEO﹣S△AEC﹣S△ABO﹣S△BCD
=3×4﹣×2×4﹣×1×2﹣×2×3
=12﹣4﹣1﹣3
=4.
(2)设点P的坐标为(x,0),则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4.
解得:x=10或x=﹣6.
所以点P的坐标为(10,0)或(﹣6,0).
22.解:(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
23.解:(1)C(0,2),D(4,2)
S四边形ABDC=AB OC=4×2=8;
(2)存在,当BF=CD时,三角形DFC的面积是三角形DFB面积的2倍.
∵C(0,2),D(4,2),
∴CD=4,BF=CD=2.
∵B(3,0),
∴F(1,0)或(5,0).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
