2021-2022学年北师大版九年级数学下册3.1圆同步达标测试(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1圆同步达标测试(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览



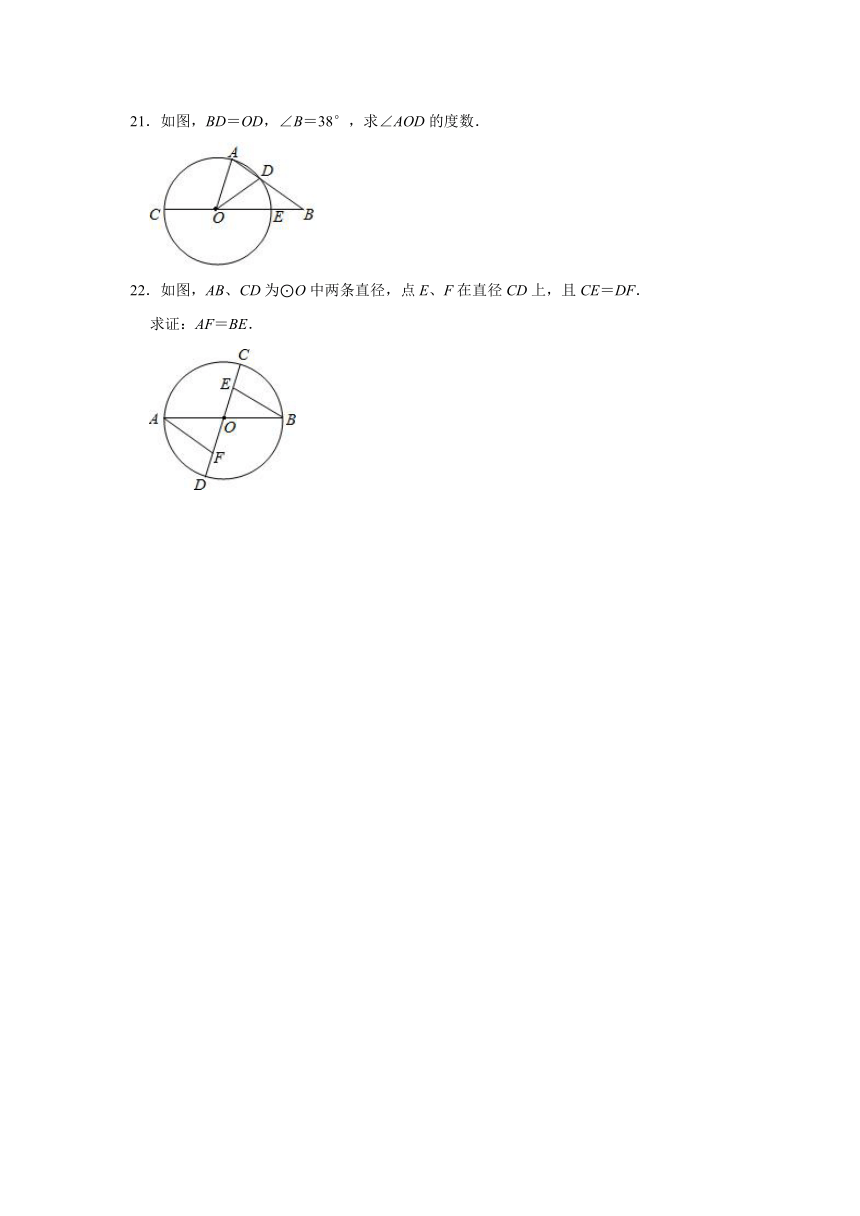

文档简介
2021-2022学年北师大版九年级数学下册《3.1圆》同步达标测试(附答案)
一.选择题(共9小题,满分36分)
1.下列说法正确的是( )
A.弦是直径 B.弧是半圆
C.直径是圆中最长的弦 D.半圆是圆中最长的弧
2.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm B.10cm C.15cm D.20cm
3.已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
4.已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
5.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地 B.老鼠先到达B地
C.猫和老鼠同时到达B地 D.无法确定
6.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
7.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
8.现有两个圆,⊙O1的半径等于篮球的半径,⊙O2的半径等于一个乒乓球的半径,现将两个圆的周长都增加1米,则面积增加较多的圆是( )
A.⊙O1 B.⊙O2 C.两圆增加的面积是相同的 D.无法确定
9.已知AB是⊙O的弦,⊙O的半径为r,下列关系式一定成立的是( )
A.AB>r B.AB<r C.AB<2r D.AB≤2r
二.填空题(共8小题,满分40分)
10.已知线段AB=6cm,则经过A、B两点的最小的圆的半径为 .
11.已知,圆A的周长是圆B的周长的4倍,那么圆A的面积是圆B的面积的 倍.
12.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
13.如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为 .
14.如图,正方形ABCD的边长为1,其中,,的圆心依次是点A,B,C.连接GB和FD,则GB与FD的关系是 .
15.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
16.如图,若点O为⊙O的圆心,则线段 是圆O的半径;线段 是圆O的弦,其中最长的弦是 ; 是劣弧; 是半圆.
17.已知⊙O的半径为3cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数的值有 个,这样的弦共有 条.
三.解答题(共5小题,满分44分)
18.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
19.如图,点P为⊙O外一点,PO及延长线分别交⊙O于A、B,过点P作一直线交⊙O于M、N(异于A、B).求证:
(1)AB>MN; (2)PB>PN; (3)PA<PM.
20.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
21.如图,BD=OD,∠B=38°,求∠AOD的度数.
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
一.选择题(共9小题,满分36分)
1.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
2.解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
3.解:∵点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,
∴点C可以在圆O1的内部,故A错误,B正确;
∵过点B、C的圆记作为圆O2,
∴点A可以在圆O2的外部,故C错误;
∵过点C、A的圆记作为圆O3,
∴点B可以在圆O3的外部,故D错误.
故选:B.
4.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
5.解:以AB为直径的半圆的长是:π AB;
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:a+πb+πc+πd=π(a+b+c+d)=π AB.
故猫和老鼠行走的路径长相同.
故选:C.
6.解:图中的弦有AB,BC,CE共三条,
故选:B.
7.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
8.解:设⊙O1的半径等于R,变大后的半径等于R′;⊙O2的半径等于r,变大后的半径等于r′,其中R>r.
由题意得,2πR+1=2πR′,2πr+1=2πr′,
解得R′=R+,r′=r+;
所以R′﹣R=,r′﹣r=,
所以,两圆的半径伸长是相同的,且两圆的半径都伸长.
∴⊙O1的面积=πR2,变大后的面积=,面积增加了﹣πR2=R+,
⊙O2的面积=πr2,变大后的面积=,面积增加了=r+,
∵R>r,
∴R+>r+,
∴⊙O1的面积增加的多.
故选:A.
9.解:若AB是⊙O的直径时,AB=2r.
若AB不是⊙O的直径时,AB<2r,无法判定AB与r的大小关系.
观察选项,选项D符合题意.
故选:D.
二.填空题(共8小题,满分40分)
10.解:根据题意得:经过线段AB最小的圆即为以AB为直径的圆,
则此时半径为3cm.
故答案为:3cm.
11.解:设圆A的半径为a,圆B的半径为b.
由题意2πa=4×2πb,
∴a=4b,
∴⊙A的面积:⊙B的面积=π (4b)2:πb2=16:1.
故答案为16
12.解:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°﹣∠M﹣∠N=80°,
故答案为80°.
13.解:∵AB为圆的直径,
∴AB=4,
∴当点O到AB的距离最大时,△AOB的面积的最大值,
即OM⊥AB时,△AOB的面积的最大值,最大值为×3×4=6.
故答案为6.
14.证明:∵BC=DC,CG=CF,又∠FCD=∠GCB=90°,
∴△FCD≌△GCB,
∴GB=FD,∠G=∠F,
∴∠G+∠CDF=∠F+∠CDF=90°,
即GB与FD的关系是相等且互相垂直.
故填空答案:相等且互相垂直.
15.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
16.解:如图,若点O为⊙O的圆心,则线段OA、OB、OC是圆O的半径;线段AC、AB、BC是圆O的弦,其中最长的弦是AC;、是劣弧;、是半圆.
故答案为OA、OB、OC;AC、AB、BC;AC;、;、;
17.解:∵⊙O的半径为3cm,
∴直径AB=6cm,
∴弦长的整数值有1,2,3,4,5,6六种可能,
这样的弦共有11条,
故答案为6,11.
三.解答题(共5小题,满分44分)
18.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
19.证明:连接AM、AN
∵AB为直径,MN为不过圆心的弦
∴AB>MN(圆中弦直径最大)
∵AB为直径
∴∠ANB=90°
∴∠PNB=∠ANB+∠PNA>90°
∴∠PNB为钝角
∴PB>PN(大角对大边)
∵四边形AMNB内接于圆O
∴∠PAM=∠PNB为钝角
∴PA<PM
20.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
21.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
一.选择题(共9小题,满分36分)
1.下列说法正确的是( )
A.弦是直径 B.弧是半圆
C.直径是圆中最长的弦 D.半圆是圆中最长的弧
2.已知⊙O的半径是5cm,则⊙O中最长的弦长是( )
A.5cm B.10cm C.15cm D.20cm
3.已知点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,过点B、C的圆记作为圆O2,过点C、A的圆记作为圆O3,则下列说法中正确的是( )
A.圆O1可以经过点C B.点C可以在圆O1的内部
C.点A可以在圆O2的内部 D.点B可以在圆O3的内部
4.已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
5.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地 B.老鼠先到达B地
C.猫和老鼠同时到达B地 D.无法确定
6.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
7.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm B.等于12cm C.小于6cm D.大于12cm
8.现有两个圆,⊙O1的半径等于篮球的半径,⊙O2的半径等于一个乒乓球的半径,现将两个圆的周长都增加1米,则面积增加较多的圆是( )
A.⊙O1 B.⊙O2 C.两圆增加的面积是相同的 D.无法确定
9.已知AB是⊙O的弦,⊙O的半径为r,下列关系式一定成立的是( )
A.AB>r B.AB<r C.AB<2r D.AB≤2r
二.填空题(共8小题,满分40分)
10.已知线段AB=6cm,则经过A、B两点的最小的圆的半径为 .
11.已知,圆A的周长是圆B的周长的4倍,那么圆A的面积是圆B的面积的 倍.
12.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
13.如图,平面直角坐标系xOy中,M点的坐标为(3,0),⊙M的半径为2,过M点的直线与⊙M的交点分别为A、B,则△AOB的面积的最大值为 .
14.如图,正方形ABCD的边长为1,其中,,的圆心依次是点A,B,C.连接GB和FD,则GB与FD的关系是 .
15.如图,A,B,C是⊙O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
16.如图,若点O为⊙O的圆心,则线段 是圆O的半径;线段 是圆O的弦,其中最长的弦是 ; 是劣弧; 是半圆.
17.已知⊙O的半径为3cm,A为⊙O上一定点,P在⊙O上沿圆周运动(不与A重合),则弦AP的长度为整数的值有 个,这样的弦共有 条.
三.解答题(共5小题,满分44分)
18.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=20°,AE交⊙O于点B,且AB=OC.
(1)求∠AOB的度数.
(2)求∠EOD的度数.
19.如图,点P为⊙O外一点,PO及延长线分别交⊙O于A、B,过点P作一直线交⊙O于M、N(异于A、B).求证:
(1)AB>MN; (2)PB>PN; (3)PA<PM.
20.如图,已知AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D,AD<BD,若CD=2cm,AB=5cm,求AD、AC的长.
21.如图,BD=OD,∠B=38°,求∠AOD的度数.
22.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
参考答案
一.选择题(共9小题,满分36分)
1.解:A、直径是弦,但弦不一定是直径,故错误,不符合题意;
B、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
C、直径是圆中最长的弦,正确,符合题意;
D、半圆是小于优弧而大于劣弧的弧,故错误,不符合题意,
故选:C.
2.解:∵⊙O的半径是5cm,
∴⊙O中最长的弦,即直径的长为10cm,
故选:B.
3.解:∵点C在线段AB上(点C与点A、B不重合),过点A、B的圆记作为圆O1,
∴点C可以在圆O1的内部,故A错误,B正确;
∵过点B、C的圆记作为圆O2,
∴点A可以在圆O2的外部,故C错误;
∵过点C、A的圆记作为圆O3,
∴点B可以在圆O3的外部,故D错误.
故选:B.
4.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
5.解:以AB为直径的半圆的长是:π AB;
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:a+πb+πc+πd=π(a+b+c+d)=π AB.
故猫和老鼠行走的路径长相同.
故选:C.
6.解:图中的弦有AB,BC,CE共三条,
故选:B.
7.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
8.解:设⊙O1的半径等于R,变大后的半径等于R′;⊙O2的半径等于r,变大后的半径等于r′,其中R>r.
由题意得,2πR+1=2πR′,2πr+1=2πr′,
解得R′=R+,r′=r+;
所以R′﹣R=,r′﹣r=,
所以,两圆的半径伸长是相同的,且两圆的半径都伸长.
∴⊙O1的面积=πR2,变大后的面积=,面积增加了﹣πR2=R+,
⊙O2的面积=πr2,变大后的面积=,面积增加了=r+,
∵R>r,
∴R+>r+,
∴⊙O1的面积增加的多.
故选:A.
9.解:若AB是⊙O的直径时,AB=2r.
若AB不是⊙O的直径时,AB<2r,无法判定AB与r的大小关系.
观察选项,选项D符合题意.
故选:D.
二.填空题(共8小题,满分40分)
10.解:根据题意得:经过线段AB最小的圆即为以AB为直径的圆,
则此时半径为3cm.
故答案为:3cm.
11.解:设圆A的半径为a,圆B的半径为b.
由题意2πa=4×2πb,
∴a=4b,
∴⊙A的面积:⊙B的面积=π (4b)2:πb2=16:1.
故答案为16
12.解:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°﹣∠M﹣∠N=80°,
故答案为80°.
13.解:∵AB为圆的直径,
∴AB=4,
∴当点O到AB的距离最大时,△AOB的面积的最大值,
即OM⊥AB时,△AOB的面积的最大值,最大值为×3×4=6.
故答案为6.
14.证明:∵BC=DC,CG=CF,又∠FCD=∠GCB=90°,
∴△FCD≌△GCB,
∴GB=FD,∠G=∠F,
∴∠G+∠CDF=∠F+∠CDF=90°,
即GB与FD的关系是相等且互相垂直.
故填空答案:相等且互相垂直.
15.解:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°,
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
故答案为140°.
16.解:如图,若点O为⊙O的圆心,则线段OA、OB、OC是圆O的半径;线段AC、AB、BC是圆O的弦,其中最长的弦是AC;、是劣弧;、是半圆.
故答案为OA、OB、OC;AC、AB、BC;AC;、;、;
17.解:∵⊙O的半径为3cm,
∴直径AB=6cm,
∴弦长的整数值有1,2,3,4,5,6六种可能,
这样的弦共有11条,
故答案为6,11.
三.解答题(共5小题,满分44分)
18.解:(1)连OB,如图,
∵AB=OC,OB=OC,
∴AB=BO,
∴∠AOB=∠1=∠A=20°;
(2)∵∠2=∠A+∠1,
∴∠2=2∠A,
∵OB=OE,
∴∠2=∠E,
∴∠E=2∠A,
∴∠DOE=∠A+∠E=3∠A=60°.
19.证明:连接AM、AN
∵AB为直径,MN为不过圆心的弦
∴AB>MN(圆中弦直径最大)
∵AB为直径
∴∠ANB=90°
∴∠PNB=∠ANB+∠PNA>90°
∴∠PNB为钝角
∴PB>PN(大角对大边)
∵四边形AMNB内接于圆O
∴∠PAM=∠PNB为钝角
∴PA<PM
20.解:连接OC,
∵AB=5cm,
∴OC=OA=AB=cm,
Rt△CDO中,由勾股定理得:DO==cm,
∴AD=﹣=1cm,
由勾股定理得:AC==,
则AD的长为1cm,AC的长为cm.
21.解:∵BD=OD,∠B=38°,
∴∠DOB=∠B=38°,
∴∠ADO=∠DOB+∠B=2×38°=76°,
∵OA=OD,
∴∠A=∠ADO=76°,
∴∠AOD=180°﹣∠A﹣∠ADO=180°﹣76°﹣76°=28°.
22.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
