2021-2022学年苏科版九年级数学上册 3.2中位数与众数 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册 3.2中位数与众数 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 432.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 08:16:55 | ||
图片预览




文档简介
3.2中位数与众数-同步练习
一、单选题
1.某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81,该组数据的中位数是( )
A.78 B.81 C.91 D.77.3
2.对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的中位数是( )
A.6 B.7 C.8 D.9
4.某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A.服装型号的平均数 B.服装型号的众数
C.服装型号的中位数 D.最小的服装型号
5.把5个整数从小到大排列,其中位数是4,最大数是6,则这5个整数可能的最大的和是( )
A.21 B.22 C.23 D.24
6.一组数据的众数是,则这组数据的中位数是( )
A. B. C. D.
7.5个整数从小到大的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是( )
A.21 B.22 C.23 D.24
8.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
二、填空题
9.五个正整数,中位数是4,众数是6,这五个正整数的和为__________________________.
10.已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是_____.
11.已知一组数据:x,10,12,6的中位数与平均数相等,则x的值是__________.
12.若干名同学制作迎奥运卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为 .
13.在一次信息技术考试中,抽得6名学生的成绩(单位:分)如下:8,6,7,x,10,9,已知这组数据的平均数是8,则这组数据的中位数是 .
14.下表是某养殖户的500只鸡出售时质量的统计数据.
则500只鸡质量的中位数为 .
15.五个正整数,中位数是4,众数是6,这五个正整数的和为__________________________.
三、解答题
16.在高速公路上的一个测速点,仪器记录下过往车辆的行驶速度(单位:千米/时),分析人员随机选取了10个速度数据如下:98,99,102,105,97,86,105,110,95,91.求这组数据的平均数、中位数和众数.
17.车间有20名工人,某一天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,
从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
18.某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取50名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩(数据分7组:60≤x<80,80≤x<100,…,180≤x<200)在100≤x<120这一组的是:
根据以上信息,回答下列问题:
(1)表中a= ;
(2)在这次测试中,七年级甲同学的成绩122次,八年级乙同学的成绩125次,他们的测试成绩,在各自年级所抽取的50名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
(3)该校七年级共有500名学生,估计一分钟跳绳不低于116次的有多少人?
19.为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
20.为了提高农民收入,村干部带领村民自愿投资办起了一个养鸡场.办场时买来的1000只小鸡,经过一段时间精心饲养,可以出售了,下表是这些鸡出售时质量的统计数据.
质量/ 1.0 1.2 1.5 1.8 2
频数 112 226 323 241 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位)?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
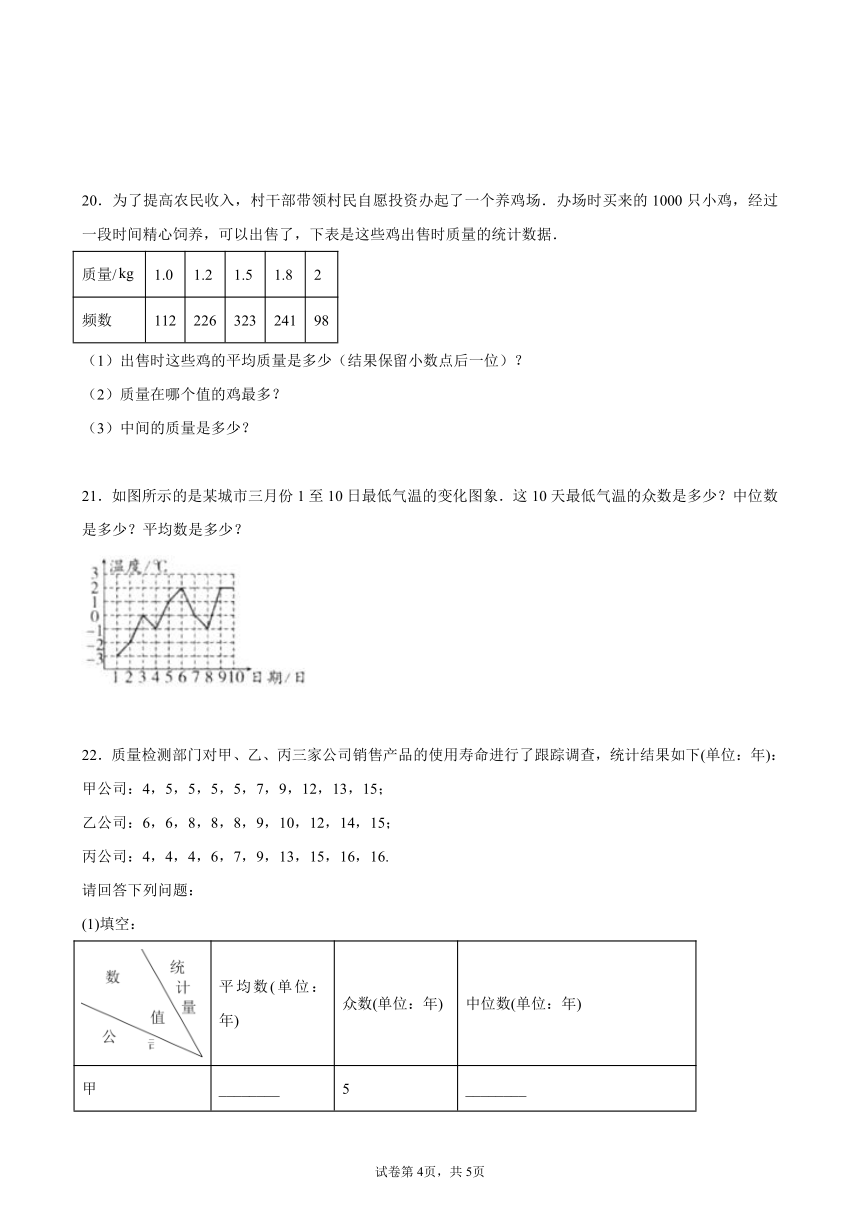
21.如图所示的是某城市三月份1至10日最低气温的变化图象.这10天最低气温的众数是多少?中位数是多少?平均数是多少?
22.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 ________ 5 ________
乙 9.6 ________ 8.5
丙 9.4 4 ________
如果你是顾客,你将选购哪家公司销售的产品,为什么?
23.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 ________ 5 ________
乙 9.6 ________ 8.5
丙 9.4 4 ________
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
24.某中学数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
(1)求这30户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为(吨),家庭月用水量不超过(吨)的部分按原价收费,超过(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:将这组数据重新排列为:56、61、70、75、75、81、81、91、91、92,
则其中位数为=78,
故选:A.
2.A
【解析】将这组数据从小到大排列为:2,2,3,3,3,3,3,3,6,6,10,共11个数,所以第6个数据是中位数,即中位数为3.
数据3的个数为6,所以众数为3.
平均数为,
由此可知(1)正确,(2)、(3)、(4)均错误,
故选A.
3.C
【解析】将这组数据重新排序为6,7,8,9,9,
∴中位数是按从小到大排列后第3个数为:8.
故选C.
4.B
【解析】解:由于众数是数据中出现最多的数,销售商最感兴趣的是服装型号的销售量哪个最大,所以他最应该关注的是众数.
故选B
5.D
【解析】根据中位数的定义5个整数从小到大排列时,其中位数为4,则前两个数最大是4,4.∵最大数是6,可知后两个数最大为6,6.这5个整数最大为:4,4,4,6,6,∴这5个整数可能的最大的和是24.
故选D.
6.B
【解析】解:这组数据的众数,
,
将数据从小到大排列为:
则中位数为:.
故选B.
7.A
【解析】由题意知,和最大时这五个整数为2,3,4,6,6,它们的和是21.
8.A
【解析】解:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,这组数据的众数为:5;中位数为:4
故选:A.
9.19或20或21
【解析】∵五个正整数,中位数是4,众数是6,
∴五个正整数为:6,6,4,3,2或6,6,4,3,1或6,6,4,2,1,
∴这五个正整数和为19或20或21.
10.5
【解析】∵一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,
∴(2+5+x+y+2x+11)=(x+y)=7,
解得y=9,x=5,
∴这组数据的众数是5.
故正确答案为:5.
11.4或8或16
【解析】(1)将这组数据从大到小的顺序排列为12,10,x,6,
处于中间位置的数是10,x,
那么由中位数的定义可知,这组数据的中位数是(10+x)÷2,
平均数为(12+10+x+6)÷4,
∵数据12,10,x,6,的中位数与平均数相等,
∴(10+x)÷2=(12+10+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后12,10,6,x,
中位数是(10+6)÷2=8,
此时平均数是(12+10+x+6)÷4=8,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,12,10,6,
中位数是(12+10)÷2=11,
平均数(x+12+10+6)÷4=11,
解得x=16,符合排列顺序.
∴x的值为4、8或16.
故答案为4或8或16.
12.答案为:b>a>c.
13.答案为:8.
14.答案为:1.4kg.
15.19或20或21
【解析】∵五个正整数,中位数是4,众数是6,
∴五个正整数为:6,6,4,3,2或6,6,4,3,1或6,6,4,2,1,
∴这五个正整数和为19或20或21.
16.平均数为98.8,.中位数为98.5,众数为105
【解析】这组数据的平均数为.将这10个数据从小到大排列后,最中间两个位置上的数为98,99,∴中位数为.这10个数据中,105出现了2次,出现的次数最多,∴众数为105.
17解得:x=4.
故答案为4.17.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)中位数为=12(个),众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
18.解:(1)∵七年级50名学生成绩的中位数是第25、26个数据的平均数,
而第25、26个数据分别是117、119,
∴中位数a==118,故答案为:118;
(2)∴在各自年级所抽取的50名同学中,排名更靠前的是甲,
理由是甲的成绩122超过中位数118,乙的成绩125低于其中位数126,
故答案为:甲,甲的成绩122超过中位数118,乙的成绩125低于其中位数126.
(3)估计一分钟跳绳不低于116次的有500×=270(人).
19.解:(1)调查的总人数是10÷20%=50(人);
(2)户外活动时间是1.5小时的人数是50×24%=12(人),
;
(3)中数是1小时,中位数是1小时;
(4)学生户外活动的平均时间符合要求的人数是20000×(1﹣20%)=16000(人).
答:大约有16000学生户外活动的平均时间符合要求.
20.(1)出售时这些鸡的平均质量是;(2)质量在哪个值的鸡最多是;(3)中间的质量是.
【解析】(1)出售时这些鸡的平均质量是:
(2)由表知,重量为的鸡的数量最多;
(3)把鸡的质量按从小到大排列,正中间的两只鸡的质量应该是第500、501个数,而112+226=338,112+226+323=661>500,因此正中间两只鸡的质量的平均数是1.5kg,从而中间的质量是.
21.这10天最低气温的众数是2℃,中位数和平均数都是0℃.
【解析】解:从图中可以看出,这10天的最低气温分别是℃,℃,0℃,℃,1℃,2℃,0℃,℃,2℃,2℃.其中2℃出现了3次,出现次数最多,所以这10天最低气温的众数是2℃;
把最低气温从低到高排列,第五个数据是0℃,第六个数据也是0℃,因此,该组数据的中位数是0℃;
这10个数据的平均数.所以这10天最低气温的众数是2℃,中位数和平均数都是0℃,
22.(1)填表见解析;(2)乙公司,理由见解析.
【解析】(1)甲公司:平均数为,中位数是6;
乙公司:众数为8;
丙公司:中位数为8.
填表如下:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 __8__ 5 __6__
乙 9.6 __8__ 8.5
丙 9.4 4 __8__
(2)乙公司.因为从平均数、众数和中位数三项指标上看,乙公司都比其他两个公司要好,所以乙公司的产品质量更高.
23.(1)填表见解析;(2)乙公司,理由见解析.
【解析】(1)甲公司:平均数为,中位数是6;
乙公司:众数为8;
丙公司:中位数为8.
填表如下:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 __8__ 5 __6__
乙 9.6 __8__ 8.5
丙 9.4 4 __8__
(2)乙公司.因为从平均数、众数和中位数三项指标上看,乙公司都比其他两个公司要好,所以乙公司的产品质量更高.
24.(1)众数是7,中位数是7;(2)9300吨;(3)以中位数或众数作为月基本用水量较为合理.
【解析】(1)解:,
众数是7,中位数是7
(2)(吨)
∴该社区月用水量约为9300吨
(3)以中位数或众数作为月基本用水量较为合理.
因为这样既可满足大多数家庭的月用水量,也可以引导用水量高于7吨的家庭节约用水.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某市在一次空气污染指数抽查中,收集到10天的数据如下:61,75,70,56,81,91,92,91,75,81,该组数据的中位数是( )
A.78 B.81 C.91 D.77.3
2.对于数据3,3,2,3,6,3,10,3,6,3,2.①这组数据的众数是3;②这组数据的众数与中位数的数值不等;③这组数据的中位数与平均数的数值相等;④这组数据的平均数与众数的数值相等,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
3.一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的中位数是( )
A.6 B.7 C.8 D.9
4.某服装销售商在进行市场占有率的调查时,他最应该关注的是( )
A.服装型号的平均数 B.服装型号的众数
C.服装型号的中位数 D.最小的服装型号
5.把5个整数从小到大排列,其中位数是4,最大数是6,则这5个整数可能的最大的和是( )
A.21 B.22 C.23 D.24
6.一组数据的众数是,则这组数据的中位数是( )
A. B. C. D.
7.5个整数从小到大的排列,其中位数是4,如果这组数据的唯一众数是6,则这5个整数最大的和可能是( )
A.21 B.22 C.23 D.24
8.实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A.4,5 B.5,4 C.4,4 D.5,5
二、填空题
9.五个正整数,中位数是4,众数是6,这五个正整数的和为__________________________.
10.已知一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,则这组数据的众数是_____.
11.已知一组数据:x,10,12,6的中位数与平均数相等,则x的值是__________.
12.若干名同学制作迎奥运卡通图片,他们制作的卡通图片张数的条形统计图如图所示,设他们制作的卡通图片张数的平均数为a,中位数为b,众数为c,则a,b,c的大小关系为 .
13.在一次信息技术考试中,抽得6名学生的成绩(单位:分)如下:8,6,7,x,10,9,已知这组数据的平均数是8,则这组数据的中位数是 .
14.下表是某养殖户的500只鸡出售时质量的统计数据.
则500只鸡质量的中位数为 .
15.五个正整数,中位数是4,众数是6,这五个正整数的和为__________________________.
三、解答题
16.在高速公路上的一个测速点,仪器记录下过往车辆的行驶速度(单位:千米/时),分析人员随机选取了10个速度数据如下:98,99,102,105,97,86,105,110,95,91.求这组数据的平均数、中位数和众数.
17.车间有20名工人,某一天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,
从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
18.某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取50名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩(数据分7组:60≤x<80,80≤x<100,…,180≤x<200)在100≤x<120这一组的是:
根据以上信息,回答下列问题:
(1)表中a= ;
(2)在这次测试中,七年级甲同学的成绩122次,八年级乙同学的成绩125次,他们的测试成绩,在各自年级所抽取的50名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
(3)该校七年级共有500名学生,估计一分钟跳绳不低于116次的有多少人?
19.为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
20.为了提高农民收入,村干部带领村民自愿投资办起了一个养鸡场.办场时买来的1000只小鸡,经过一段时间精心饲养,可以出售了,下表是这些鸡出售时质量的统计数据.
质量/ 1.0 1.2 1.5 1.8 2
频数 112 226 323 241 98
(1)出售时这些鸡的平均质量是多少(结果保留小数点后一位)?
(2)质量在哪个值的鸡最多?
(3)中间的质量是多少?
21.如图所示的是某城市三月份1至10日最低气温的变化图象.这10天最低气温的众数是多少?中位数是多少?平均数是多少?
22.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 ________ 5 ________
乙 9.6 ________ 8.5
丙 9.4 4 ________
如果你是顾客,你将选购哪家公司销售的产品,为什么?
23.质量检测部门对甲、乙、丙三家公司销售产品的使用寿命进行了跟踪调查,统计结果如下(单位:年):
甲公司:4,5,5,5,5,7,9,12,13,15;
乙公司:6,6,8,8,8,9,10,12,14,15;
丙公司:4,4,4,6,7,9,13,15,16,16.
请回答下列问题:
(1)填空:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 ________ 5 ________
乙 9.6 ________ 8.5
丙 9.4 4 ________
(2)如果你是顾客,你将选购哪家公司销售的产品,为什么?
24.某中学数学活动小组为了调查居民的用水情况,从某社区的1500户家庭中随机抽取了30户家庭的月用水量,结果如下表所示:
月用水量(吨) 3 4 5 7 8 9 10
户数 4 3 5 11 4 2 1
(1)求这30户家庭月用水量的平均数、众数和中位数;
(2)根据上述数据,试估计该社区的月用水量;
(3)由于我国水资源缺乏,许多城市常利用分段计费的办法引导人们节约用水,即规定每个家庭的月基本用水量为(吨),家庭月用水量不超过(吨)的部分按原价收费,超过(吨)的部分加倍收费.你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理?简述理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.A
【解析】解:将这组数据重新排列为:56、61、70、75、75、81、81、91、91、92,
则其中位数为=78,
故选:A.
2.A
【解析】将这组数据从小到大排列为:2,2,3,3,3,3,3,3,6,6,10,共11个数,所以第6个数据是中位数,即中位数为3.
数据3的个数为6,所以众数为3.
平均数为,
由此可知(1)正确,(2)、(3)、(4)均错误,
故选A.
3.C
【解析】将这组数据重新排序为6,7,8,9,9,
∴中位数是按从小到大排列后第3个数为:8.
故选C.
4.B
【解析】解:由于众数是数据中出现最多的数,销售商最感兴趣的是服装型号的销售量哪个最大,所以他最应该关注的是众数.
故选B
5.D
【解析】根据中位数的定义5个整数从小到大排列时,其中位数为4,则前两个数最大是4,4.∵最大数是6,可知后两个数最大为6,6.这5个整数最大为:4,4,4,6,6,∴这5个整数可能的最大的和是24.
故选D.
6.B
【解析】解:这组数据的众数,
,
将数据从小到大排列为:
则中位数为:.
故选B.
7.A
【解析】由题意知,和最大时这五个整数为2,3,4,6,6,它们的和是21.
8.A
【解析】解:将数据从小到大排列为:1,2,3,3,4,4,5,5,5,5,这组数据的众数为:5;中位数为:4
故选:A.
9.19或20或21
【解析】∵五个正整数,中位数是4,众数是6,
∴五个正整数为:6,6,4,3,2或6,6,4,3,1或6,6,4,2,1,
∴这五个正整数和为19或20或21.
10.5
【解析】∵一组从小到大排列的数据:2,5,x,y,2x,11的平均数与中位数都是7,
∴(2+5+x+y+2x+11)=(x+y)=7,
解得y=9,x=5,
∴这组数据的众数是5.
故正确答案为:5.
11.4或8或16
【解析】(1)将这组数据从大到小的顺序排列为12,10,x,6,
处于中间位置的数是10,x,
那么由中位数的定义可知,这组数据的中位数是(10+x)÷2,
平均数为(12+10+x+6)÷4,
∵数据12,10,x,6,的中位数与平均数相等,
∴(10+x)÷2=(12+10+x+6)÷4,
解得x=8,大小位置与8对调,不影响结果,符合题意;
(2)将这组数据从大到小的顺序排列后12,10,6,x,
中位数是(10+6)÷2=8,
此时平均数是(12+10+x+6)÷4=8,
解得x=4,符合排列顺序;
(3)将这组数据从大到小的顺序排列后x,12,10,6,
中位数是(12+10)÷2=11,
平均数(x+12+10+6)÷4=11,
解得x=16,符合排列顺序.
∴x的值为4、8或16.
故答案为4或8或16.
12.答案为:b>a>c.
13.答案为:8.
14.答案为:1.4kg.
15.19或20或21
【解析】∵五个正整数,中位数是4,众数是6,
∴五个正整数为:6,6,4,3,2或6,6,4,3,1或6,6,4,2,1,
∴这五个正整数和为19或20或21.
16.平均数为98.8,.中位数为98.5,众数为105
【解析】这组数据的平均数为.将这10个数据从小到大排列后,最中间两个位置上的数为98,99,∴中位数为.这10个数据中,105出现了2次,出现的次数最多,∴众数为105.
17解得:x=4.
故答案为4.17.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)中位数为=12(个),众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
18.解:(1)∵七年级50名学生成绩的中位数是第25、26个数据的平均数,
而第25、26个数据分别是117、119,
∴中位数a==118,故答案为:118;
(2)∴在各自年级所抽取的50名同学中,排名更靠前的是甲,
理由是甲的成绩122超过中位数118,乙的成绩125低于其中位数126,
故答案为:甲,甲的成绩122超过中位数118,乙的成绩125低于其中位数126.
(3)估计一分钟跳绳不低于116次的有500×=270(人).
19.解:(1)调查的总人数是10÷20%=50(人);
(2)户外活动时间是1.5小时的人数是50×24%=12(人),
;
(3)中数是1小时,中位数是1小时;
(4)学生户外活动的平均时间符合要求的人数是20000×(1﹣20%)=16000(人).
答:大约有16000学生户外活动的平均时间符合要求.
20.(1)出售时这些鸡的平均质量是;(2)质量在哪个值的鸡最多是;(3)中间的质量是.
【解析】(1)出售时这些鸡的平均质量是:
(2)由表知,重量为的鸡的数量最多;
(3)把鸡的质量按从小到大排列,正中间的两只鸡的质量应该是第500、501个数,而112+226=338,112+226+323=661>500,因此正中间两只鸡的质量的平均数是1.5kg,从而中间的质量是.
21.这10天最低气温的众数是2℃,中位数和平均数都是0℃.
【解析】解:从图中可以看出,这10天的最低气温分别是℃,℃,0℃,℃,1℃,2℃,0℃,℃,2℃,2℃.其中2℃出现了3次,出现次数最多,所以这10天最低气温的众数是2℃;
把最低气温从低到高排列,第五个数据是0℃,第六个数据也是0℃,因此,该组数据的中位数是0℃;
这10个数据的平均数.所以这10天最低气温的众数是2℃,中位数和平均数都是0℃,
22.(1)填表见解析;(2)乙公司,理由见解析.
【解析】(1)甲公司:平均数为,中位数是6;
乙公司:众数为8;
丙公司:中位数为8.
填表如下:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 __8__ 5 __6__
乙 9.6 __8__ 8.5
丙 9.4 4 __8__
(2)乙公司.因为从平均数、众数和中位数三项指标上看,乙公司都比其他两个公司要好,所以乙公司的产品质量更高.
23.(1)填表见解析;(2)乙公司,理由见解析.
【解析】(1)甲公司:平均数为,中位数是6;
乙公司:众数为8;
丙公司:中位数为8.
填表如下:
平均数(单位:年) 众数(单位:年) 中位数(单位:年)
甲 __8__ 5 __6__
乙 9.6 __8__ 8.5
丙 9.4 4 __8__
(2)乙公司.因为从平均数、众数和中位数三项指标上看,乙公司都比其他两个公司要好,所以乙公司的产品质量更高.
24.(1)众数是7,中位数是7;(2)9300吨;(3)以中位数或众数作为月基本用水量较为合理.
【解析】(1)解:,
众数是7,中位数是7
(2)(吨)
∴该社区月用水量约为9300吨
(3)以中位数或众数作为月基本用水量较为合理.
因为这样既可满足大多数家庭的月用水量,也可以引导用水量高于7吨的家庭节约用水.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
