2021-2022学年北师大版八年级数学上册7.4平行线的性质解答题专题训练 (word版、含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册7.4平行线的性质解答题专题训练 (word版、含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 253.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 10:08:11 | ||
图片预览


文档简介
2021-2022学年北师大版八年级数学上册《7.4平行线的性质》解答题专题训练(附答案)
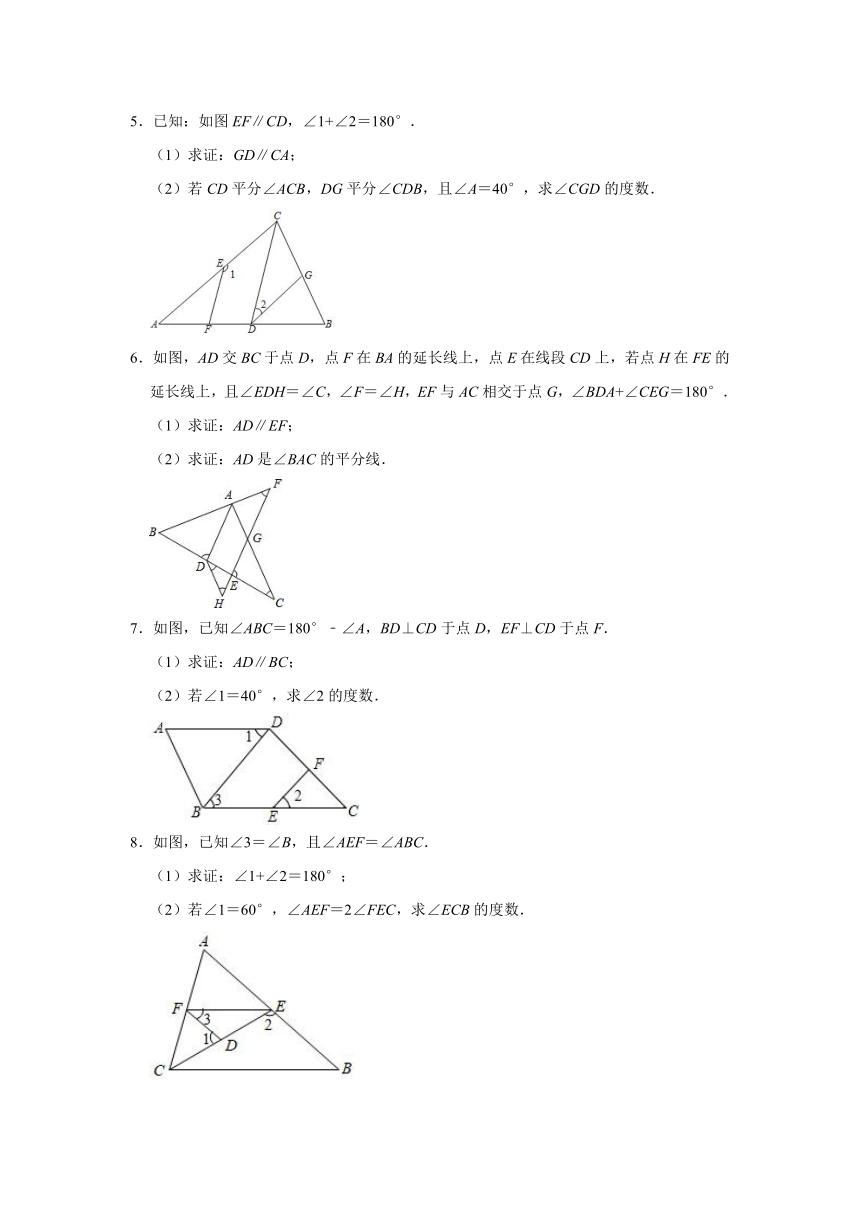
1.如图,已知∠A=∠FEC,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
2.如图,AD∥BC,∠1=∠B,∠2=∠3.
(1)求证:AB∥DE;
(2)AF与DC有什么位置关系?为什么?
(3)若∠B=68°,∠C=46°,求∠2的度数.
3.如图,已知AB∥CD,∠B=∠D,AE交BC的延长线于点E.
(1)求证:AD∥BE;
(2)若∠1=∠2=60°,∠BAC=2∠EAC,求∠DCE的度数.
4.如图,已知:AB∥CD,∠1+∠2=180°.
(1)请你判断AD与EC的位置关系,并说明理由.
(2)若CE⊥AE于点E,∠2=140°,试求∠FAB的度数.
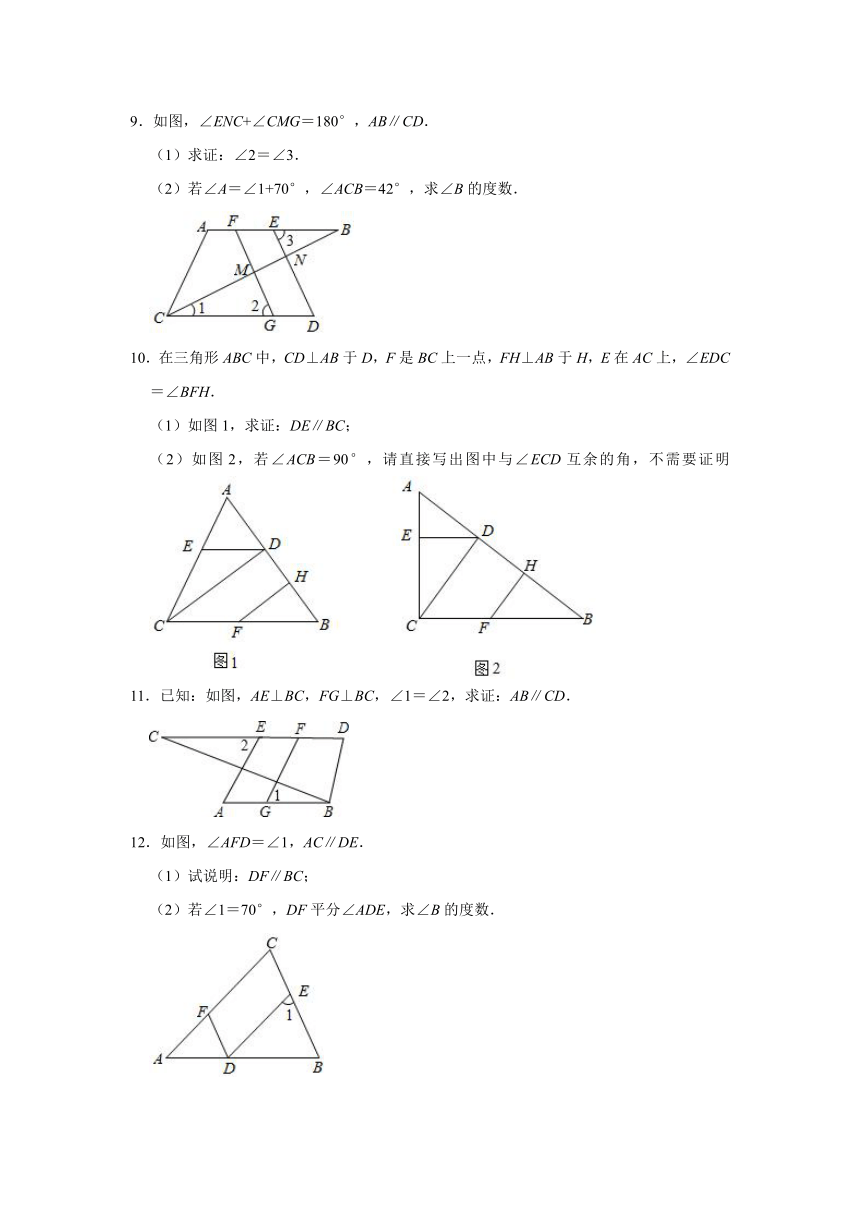
5.已知:如图EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠CGD的度数.
6.如图,AD交BC于点D,点F在BA的延长线上,点E在线段CD上,若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)求证:AD∥EF;
(2)求证:AD是∠BAC的平分线.
7.如图,已知∠ABC=180°﹣∠A,BD⊥CD于点D,EF⊥CD于点F.
(1)求证:AD∥BC;
(2)若∠1=40°,求∠2的度数.
8.如图,已知∠3=∠B,且∠AEF=∠ABC.
(1)求证:∠1+∠2=180°;
(2)若∠1=60°,∠AEF=2∠FEC,求∠ECB的度数.
9.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,求∠B的度数.
10.在三角形ABC中,CD⊥AB于D,F是BC上一点,FH⊥AB于H,E在AC上,∠EDC=∠BFH.
(1)如图1,求证:DE∥BC;
(2)如图2,若∠ACB=90°,请直接写出图中与∠ECD互余的角,不需要证明
11.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
12.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=70°,DF平分∠ADE,求∠B的度数.
13.如图,AC∥EF,∠1+∠3=180°.
(1)AF与CD是否平行?请说明理由;
(2)若AC平分∠FAB,AC⊥EB于点C,∠4=78°,求∠BCD的度数.
14.如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
15.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
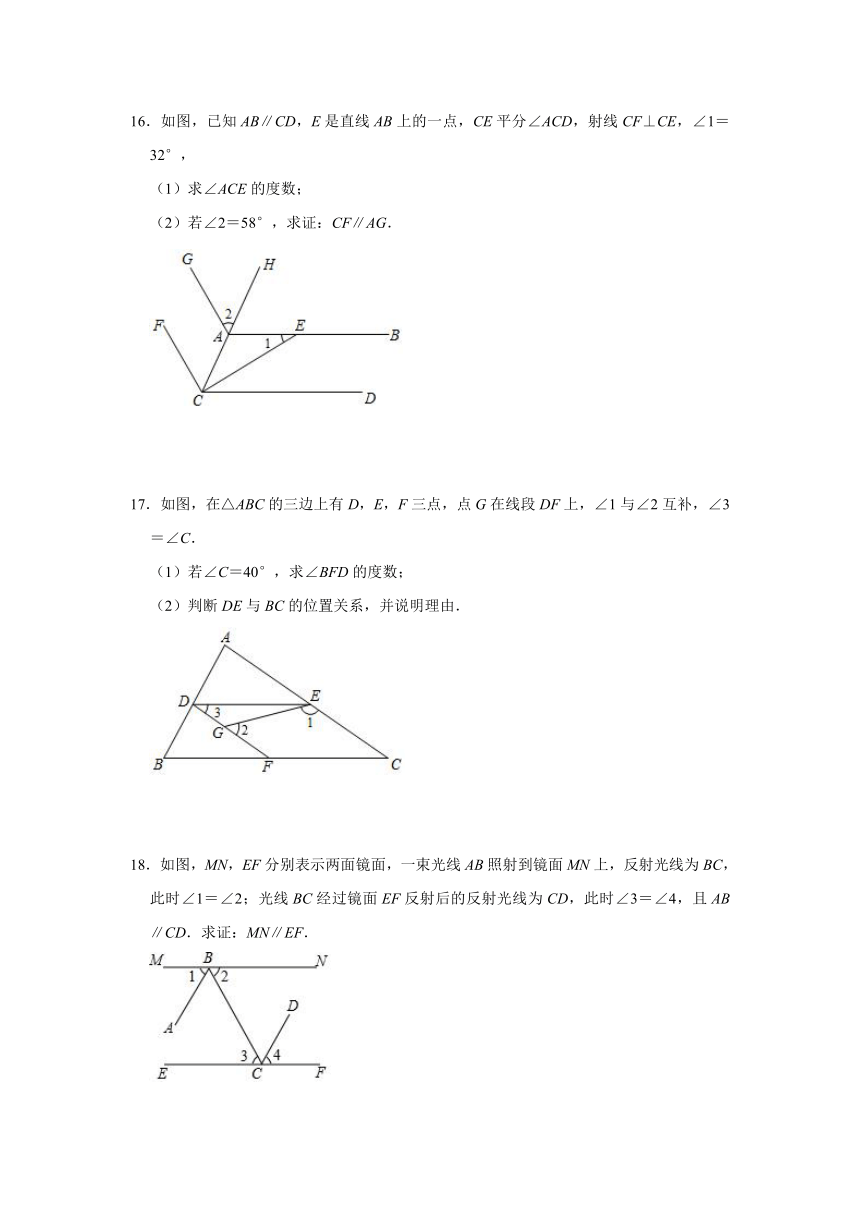
16.如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
17.如图,在△ABC的三边上有D,E,F三点,点G在线段DF上,∠1与∠2互补,∠3=∠C.
(1)若∠C=40°,求∠BFD的度数;
(2)判断DE与BC的位置关系,并说明理由.
18.如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
20.如图,已知AD∥EF,∠2=50°.
(1)求∠3的度数;
(2)若∠1=∠2,问:DG∥BA吗?请说明理由;
(3)若∠1=∠2,且∠DAG=20°,求∠AGD的度数.
21.如图,已知AD∥BC,AE平分∠BAD交BC延长线于点E,CD与AE相交于点F,∠CFE=∠E,求证:AB∥DC.
22.已知:AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证:∠BDE=∠C.
23.已知:∠BDG+∠EFG=180°,∠B=∠DEF.
(1)如图1,求证:DE∥BC.
(2)如图2,当∠A=∠EFG=90°时,请直接写出与∠C互余的角.
24.如图:AB∥CD,AE、DF分别是∠BAO、∠CDO的平分线,求证:AE∥DF.
参考答案
1.解:(1)DE∥BC,理由如下:
∵∠A=∠FEC,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(2)设∠B=x,则∠BDC=3∠B=3x,
∵DE∥BC,
∴∠ADE=∠B=x,
∵DE平分∠ADC,
∴∠ADC=2∠ADE=2x,
∴∠BDC+∠ADC=180°,
∴3x+2x=180°,
∴x=36°,
∴∠ADC=2x=72°,
∵AB∥EF,
∴∠EFC=∠ADC=72°.
2.(1)证明:∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
∵∠1=∠B(已知),
∴∠DEC=∠B(等量代换),
∴AB∥DE(同位角相等,两直线平行);
(2)解:AF∥DC,
理由如下:
∵AB∥DE(已证),
∴∠2=∠AGD(两直线平行,内错角相等),
∵∠2=∠3(已知),
∴∠AGD=∠3(等量代换),
∴AF∥DC(内错角相等,两直线平行);
(3)∵AF∥DC,∠C=46°,
∴∠AFB=∠C=46°(两直线平行,同位角相等),
∵∠B=68°,∠2+∠B+∠AFB=180°,
∴∠2=180°﹣∠B﹣∠AFB=180°﹣46°﹣68°=66°.
3.(1)证明:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)解:∵AB∥CD,∠2=60°,
∴∠BAE=∠2=60°,∠BAC=∠ACD,
∴∠EAC+∠BAC=60°,
∵∠BAC=2∠EAC,
∴∠EAC=20°,
∴∠BAC=∠ACD=40°,
∵∠1+∠ACD+∠DCE=180°,
∴∠DCE=180°﹣∠1﹣∠ACD=180°﹣60°﹣40°=80°.
4.解:(1)AD∥EC,
理由是:∵AB∥CD,
∴∠1=∠ADC,
∵∠1+∠2=180°,
∴∠2+∠ADC=180°,
∴AD∥EC;
(2)∵AD∥EC,CE⊥AE,
∴AD⊥AE,
∴∠FAD=90°,
∵∠1+∠2=180°,∠2=140°,
∴∠1=40°,
∴∠FAB=∠FAD﹣∠1=90°﹣40°=50°.
5.(1)证明:∵EF∥CD,
∴∠1+∠ECD=180°,
又∵∠1+∠2=180°,
∴∠2=∠ECD,
∴GD∥CA.
(2)解:由(1)得:GD∥CA,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠CDB,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°,
∵GD∥CA,
∴∠ACB+∠CGD=180°,
∴∠CGD=180°﹣∠ACB=180°﹣80°=100°.
6.证明:(1)∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
7.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)解:∵AD∥BC,∠1=40°,
∴∠3=∠1,
∵∠1=40°,
∴∠3=40°
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠2=∠3=40°.
8.(1)证明:∵∠3=∠B,∠AEF=∠ABC,
∴∠3=∠AEF,
∴AB∥FD,
∴∠2=∠FDE,
∵∠1+∠FDE=180°,
∴∠1+∠2=180°;
(2)解:∵∠1+∠2=180°,∠1=60°,
∴∠2=180°﹣60°=120°,
∵∠AEF=2∠FEC,∠AEF+∠FEC+∠2=180°,
∴3∠FEC+120°=180°,
∴∠FEC=20°,
∵∠AEF=∠ABC,
∴EF∥BC,
∴∠CEF=∠ECB,
∴∠ECB=20°.
9.(1)证明:∵∠ENC+∠CMG=180°,∠CMG=∠FMN,
∴∠ENC+∠FMN=180°,
∴FG∥ED,
∴∠2=∠D,
∵AB∥CD,
∴∠3=∠D,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠1+42°=180°,
∴∠1=34°,
∵AB∥CD,
∴∠B=∠1=34°.
10.(1)证明:∵FH⊥AB,CD⊥AB,
∴∠FHB=∠CDB=90°,
∴FH∥CD,
∴∠BFH=∠BCD,
又∵∠EDC=∠BFH,
∴∠BCD=∠EDC,
∴DE∥BC;
(2)解:图中与∠ECD互余的角为∠A,∠CDE,∠DCB,∠HFB.理由如下:
∵FH⊥AB,CD⊥AB,
∴∠B+∠BFH=∠B+∠BCD=90°,
∴∠BFH、∠BCD与∠B互余,
∵∠ACB=90°,
∴∠B+∠A=90°,
∴∠A与∠B互余,
∵DE∥BC,
∴∠CDE=∠BCD,
∴∠CDE与∠B互余.
∴∠BFH、∠BCD、∠A、∠CDE与∠B互余,
∵∠ECD=∠B,
∴与∠ECD互余的角有∠BFH、∠BCD、∠A、∠CDE.
11.证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
12.解:(1)∵AC∥DE,
∴∠C=∠1,
又∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=70°,DF∥BC,
∴∠EDF=∠1=70°,
又∵DF平分∠ADE,
∴∠ADF=∠EDF=70°,
∵DF∥BC,
∴∠B=∠ADF=70°.
故∠B的度数为70°.
13.解:(1)AF∥CD,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴∠3=∠4=×78°=39°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
14.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+3∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
15.证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
16.解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
17.解:(1)∵∠1与∠2互补,
∴AC∥DF,
∴∠BFD=∠C=40°;
(2)DE∥BC,理由如下:
由(1)可知:∠BFD=∠C,
∵∠C=∠3,
∴∠BFD=∠3,
∴DE∥BC.
18.证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
19.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
20.解:(1)∵AD∥EF,
∴∠3=∠2=50°;
(2)DG∥BA,理由如下:
∵∠1=∠2,∠3=∠2,
∴∠3=∠1,
∴DG∥BA;
(3)∵∠1=∠2=50°,∠GAD=20°,
∴∠AGD=180°﹣∠GAD﹣∠1=110°.
21.证明:∵AD∥BC,
∴∠2=∠E,
∵AE平分∠BAD,
∴∠1=∠2,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥DC.
22.证明:∵AD⊥BC,FG⊥BC,
∴∠ADG=∠FGC=90°,
∴AD∥FG,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴DE∥AC,
∴∠BDE=∠C.
23.(1)证明:∵∠EFD+∠EFG=180°,
∠BDG+∠EFG=180°,
∴∠BDG=∠EFD,
∴BD∥EF,
∴∠BDE+∠DEF=180°,
又∵∠DEF=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC;
(2)解:∵∠A=∠EFG=90°,
∴∠ADE+∠AED=90°,∠B+∠C=90°,
∵DE∥BC,
∴∠ADE=∠B,
∵∠B=∠DEF,
∴与∠C互余的角有∠B,∠ADE,∠DEF.
24.证明:∵AB∥CD,
∴∠BAO=∠CDO,
又∵AE、DF分别是∠BAO、∠CDO的平分线,
∴∠EAO=∠BAO=∠CDO=∠FDO,
∴AE∥DF.
1.如图,已知∠A=∠FEC,∠DEF=∠B.
(1)试判断DE与BC的位置关系,并说明理由.
(2)若DE平分∠ADC,∠BDC=3∠B,求∠EFC的度数.
2.如图,AD∥BC,∠1=∠B,∠2=∠3.
(1)求证:AB∥DE;
(2)AF与DC有什么位置关系?为什么?
(3)若∠B=68°,∠C=46°,求∠2的度数.
3.如图,已知AB∥CD,∠B=∠D,AE交BC的延长线于点E.
(1)求证:AD∥BE;
(2)若∠1=∠2=60°,∠BAC=2∠EAC,求∠DCE的度数.
4.如图,已知:AB∥CD,∠1+∠2=180°.
(1)请你判断AD与EC的位置关系,并说明理由.
(2)若CE⊥AE于点E,∠2=140°,试求∠FAB的度数.
5.已知:如图EF∥CD,∠1+∠2=180°.
(1)求证:GD∥CA;
(2)若CD平分∠ACB,DG平分∠CDB,且∠A=40°,求∠CGD的度数.
6.如图,AD交BC于点D,点F在BA的延长线上,点E在线段CD上,若点H在FE的延长线上,且∠EDH=∠C,∠F=∠H,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)求证:AD∥EF;
(2)求证:AD是∠BAC的平分线.
7.如图,已知∠ABC=180°﹣∠A,BD⊥CD于点D,EF⊥CD于点F.
(1)求证:AD∥BC;
(2)若∠1=40°,求∠2的度数.
8.如图,已知∠3=∠B,且∠AEF=∠ABC.
(1)求证:∠1+∠2=180°;
(2)若∠1=60°,∠AEF=2∠FEC,求∠ECB的度数.
9.如图,∠ENC+∠CMG=180°,AB∥CD.
(1)求证:∠2=∠3.
(2)若∠A=∠1+70°,∠ACB=42°,求∠B的度数.
10.在三角形ABC中,CD⊥AB于D,F是BC上一点,FH⊥AB于H,E在AC上,∠EDC=∠BFH.
(1)如图1,求证:DE∥BC;
(2)如图2,若∠ACB=90°,请直接写出图中与∠ECD互余的角,不需要证明
11.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
12.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=70°,DF平分∠ADE,求∠B的度数.
13.如图,AC∥EF,∠1+∠3=180°.
(1)AF与CD是否平行?请说明理由;
(2)若AC平分∠FAB,AC⊥EB于点C,∠4=78°,求∠BCD的度数.
14.如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
15.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
16.如图,已知AB∥CD,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠1=32°,
(1)求∠ACE的度数;
(2)若∠2=58°,求证:CF∥AG.
17.如图,在△ABC的三边上有D,E,F三点,点G在线段DF上,∠1与∠2互补,∠3=∠C.
(1)若∠C=40°,求∠BFD的度数;
(2)判断DE与BC的位置关系,并说明理由.
18.如图,MN,EF分别表示两面镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4,且AB∥CD.求证:MN∥EF.
已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
20.如图,已知AD∥EF,∠2=50°.
(1)求∠3的度数;
(2)若∠1=∠2,问:DG∥BA吗?请说明理由;
(3)若∠1=∠2,且∠DAG=20°,求∠AGD的度数.
21.如图,已知AD∥BC,AE平分∠BAD交BC延长线于点E,CD与AE相交于点F,∠CFE=∠E,求证:AB∥DC.
22.已知:AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,求证:∠BDE=∠C.
23.已知:∠BDG+∠EFG=180°,∠B=∠DEF.
(1)如图1,求证:DE∥BC.
(2)如图2,当∠A=∠EFG=90°时,请直接写出与∠C互余的角.
24.如图:AB∥CD,AE、DF分别是∠BAO、∠CDO的平分线,求证:AE∥DF.
参考答案
1.解:(1)DE∥BC,理由如下:
∵∠A=∠FEC,
∴AB∥EF,
∴∠DEF=∠ADE,
∵∠DEF=∠B,
∴∠ADE=∠B,
∴DE∥BC;
(2)设∠B=x,则∠BDC=3∠B=3x,
∵DE∥BC,
∴∠ADE=∠B=x,
∵DE平分∠ADC,
∴∠ADC=2∠ADE=2x,
∴∠BDC+∠ADC=180°,
∴3x+2x=180°,
∴x=36°,
∴∠ADC=2x=72°,
∵AB∥EF,
∴∠EFC=∠ADC=72°.
2.(1)证明:∵AD∥BC(已知),
∴∠1=∠DEC(两直线平行,内错角相等),
∵∠1=∠B(已知),
∴∠DEC=∠B(等量代换),
∴AB∥DE(同位角相等,两直线平行);
(2)解:AF∥DC,
理由如下:
∵AB∥DE(已证),
∴∠2=∠AGD(两直线平行,内错角相等),
∵∠2=∠3(已知),
∴∠AGD=∠3(等量代换),
∴AF∥DC(内错角相等,两直线平行);
(3)∵AF∥DC,∠C=46°,
∴∠AFB=∠C=46°(两直线平行,同位角相等),
∵∠B=68°,∠2+∠B+∠AFB=180°,
∴∠2=180°﹣∠B﹣∠AFB=180°﹣46°﹣68°=66°.
3.(1)证明:∵AB∥CD,
∴∠B=∠DCE,
∵∠B=∠D,
∴∠DCE=∠D,
∴AD∥BE;
(2)解:∵AB∥CD,∠2=60°,
∴∠BAE=∠2=60°,∠BAC=∠ACD,
∴∠EAC+∠BAC=60°,
∵∠BAC=2∠EAC,
∴∠EAC=20°,
∴∠BAC=∠ACD=40°,
∵∠1+∠ACD+∠DCE=180°,
∴∠DCE=180°﹣∠1﹣∠ACD=180°﹣60°﹣40°=80°.
4.解:(1)AD∥EC,
理由是:∵AB∥CD,
∴∠1=∠ADC,
∵∠1+∠2=180°,
∴∠2+∠ADC=180°,
∴AD∥EC;
(2)∵AD∥EC,CE⊥AE,
∴AD⊥AE,
∴∠FAD=90°,
∵∠1+∠2=180°,∠2=140°,
∴∠1=40°,
∴∠FAB=∠FAD﹣∠1=90°﹣40°=50°.
5.(1)证明:∵EF∥CD,
∴∠1+∠ECD=180°,
又∵∠1+∠2=180°,
∴∠2=∠ECD,
∴GD∥CA.
(2)解:由(1)得:GD∥CA,
∴∠BDG=∠A=40°,∠ACD=∠2,
∵DG平分∠CDB,
∴∠2=∠BDG=40°,
∴∠ACD=∠2=40°,
∵CD平分∠ACB,
∴∠ACB=2∠ACD=80°,
∵GD∥CA,
∴∠ACB+∠CGD=180°,
∴∠CGD=180°﹣∠ACB=180°﹣80°=100°.
6.证明:(1)∵∠BDA+∠CEG=180°,∠BDA+∠CDA=180°,
∴∠CEG=∠CDA,
∴AD∥EF;
(2)∵∠EDH=∠C,
∴DH∥AC,
∴∠H=∠EGC,
∵∠F=∠H,
∴∠F=∠EGC,
∵AD∥EF,
∴∠BAD=∠F,∠CAD=∠EGC,
∴∠BAD=∠CAD,
∴AD平分∠BAC.
7.(1)证明:∵∠ABC=180°﹣∠A,
∴∠ABC+∠A=180°,
∴AD∥BC;
(2)解:∵AD∥BC,∠1=40°,
∴∠3=∠1,
∵∠1=40°,
∴∠3=40°
∵BD⊥CD,EF⊥CD,
∴BD∥EF,
∴∠2=∠3=40°.
8.(1)证明:∵∠3=∠B,∠AEF=∠ABC,
∴∠3=∠AEF,
∴AB∥FD,
∴∠2=∠FDE,
∵∠1+∠FDE=180°,
∴∠1+∠2=180°;
(2)解:∵∠1+∠2=180°,∠1=60°,
∴∠2=180°﹣60°=120°,
∵∠AEF=2∠FEC,∠AEF+∠FEC+∠2=180°,
∴3∠FEC+120°=180°,
∴∠FEC=20°,
∵∠AEF=∠ABC,
∴EF∥BC,
∴∠CEF=∠ECB,
∴∠ECB=20°.
9.(1)证明:∵∠ENC+∠CMG=180°,∠CMG=∠FMN,
∴∠ENC+∠FMN=180°,
∴FG∥ED,
∴∠2=∠D,
∵AB∥CD,
∴∠3=∠D,
∴∠2=∠3;
(2)解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=∠1+70°,∠ACB=42°,
∴∠1+70°+∠1+42°=180°,
∴∠1=34°,
∵AB∥CD,
∴∠B=∠1=34°.
10.(1)证明:∵FH⊥AB,CD⊥AB,
∴∠FHB=∠CDB=90°,
∴FH∥CD,
∴∠BFH=∠BCD,
又∵∠EDC=∠BFH,
∴∠BCD=∠EDC,
∴DE∥BC;
(2)解:图中与∠ECD互余的角为∠A,∠CDE,∠DCB,∠HFB.理由如下:
∵FH⊥AB,CD⊥AB,
∴∠B+∠BFH=∠B+∠BCD=90°,
∴∠BFH、∠BCD与∠B互余,
∵∠ACB=90°,
∴∠B+∠A=90°,
∴∠A与∠B互余,
∵DE∥BC,
∴∠CDE=∠BCD,
∴∠CDE与∠B互余.
∴∠BFH、∠BCD、∠A、∠CDE与∠B互余,
∵∠ECD=∠B,
∴与∠ECD互余的角有∠BFH、∠BCD、∠A、∠CDE.
11.证明:∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNM=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
12.解:(1)∵AC∥DE,
∴∠C=∠1,
又∵∠AFD=∠1,
∴∠C=∠AFD,
∴DF∥BC.
(2)∵∠1=70°,DF∥BC,
∴∠EDF=∠1=70°,
又∵DF平分∠ADE,
∴∠ADF=∠EDF=70°,
∵DF∥BC,
∴∠B=∠ADF=70°.
故∠B的度数为70°.
13.解:(1)AF∥CD,
理由如下:
∵AC∥EF,
∴∠1+∠2=180°,
又∵∠1+∠3=180°,
∴∠2=∠3,
∴FA∥CD;
(2)∵AC平分∠FAB,
∴∠2=∠CAD,
∵∠2=∠3,
∴∠CAD=∠3,
∵∠4=∠3+∠CAD,
∴∠3=∠4=×78°=39°,
∵EF⊥BE,AC∥EF,
∴AC⊥BE,
∴∠ACB=90°,
∴∠BCD=90°﹣∠3=51°.
14.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+3∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
15.证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
16.解:(1)∵AB∥CD,
∴∠1=∠DCE=32°,
∵CE平分∠ACD,
∴∠ACE=∠DCE=32°;
(2)∵CF⊥CE,
∴∠FCE=90°,
∴∠FCH=90°﹣32°=58°,
∵∠2=58°,
∴∠FCH=∠2,
∴CF∥AG.
17.解:(1)∵∠1与∠2互补,
∴AC∥DF,
∴∠BFD=∠C=40°;
(2)DE∥BC,理由如下:
由(1)可知:∠BFD=∠C,
∵∠C=∠3,
∴∠BFD=∠3,
∴DE∥BC.
18.证明:∵AB∥CD,
∴∠ABC=∠BCD,
∵∠1+∠ABC+∠2=∠3+∠BCD+∠4=180°,
∴∠1+∠2=∠3+∠4,
又∵∠1=∠2,∠3=∠4,
∴∠2=∠3,
∴MN∥EF.
19.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
20.解:(1)∵AD∥EF,
∴∠3=∠2=50°;
(2)DG∥BA,理由如下:
∵∠1=∠2,∠3=∠2,
∴∠3=∠1,
∴DG∥BA;
(3)∵∠1=∠2=50°,∠GAD=20°,
∴∠AGD=180°﹣∠GAD﹣∠1=110°.
21.证明:∵AD∥BC,
∴∠2=∠E,
∵AE平分∠BAD,
∴∠1=∠2,
∴∠1=∠E,
∵∠CFE=∠E,
∴∠1=∠CFE,
∴AB∥DC.
22.证明:∵AD⊥BC,FG⊥BC,
∴∠ADG=∠FGC=90°,
∴AD∥FG,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴DE∥AC,
∴∠BDE=∠C.
23.(1)证明:∵∠EFD+∠EFG=180°,
∠BDG+∠EFG=180°,
∴∠BDG=∠EFD,
∴BD∥EF,
∴∠BDE+∠DEF=180°,
又∵∠DEF=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC;
(2)解:∵∠A=∠EFG=90°,
∴∠ADE+∠AED=90°,∠B+∠C=90°,
∵DE∥BC,
∴∠ADE=∠B,
∵∠B=∠DEF,
∴与∠C互余的角有∠B,∠ADE,∠DEF.
24.证明:∵AB∥CD,
∴∠BAO=∠CDO,
又∵AE、DF分别是∠BAO、∠CDO的平分线,
∴∠EAO=∠BAO=∠CDO=∠FDO,
∴AE∥DF.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
