2021-2022学年北师大版八年级数学上册7.5三角形的内角和 选择专项练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册7.5三角形的内角和 选择专项练习(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 206.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览


文档简介
2021-2022学年北师大版八年级数学上册《7.5三角形的内角和》选择专项练习(附答案)
1.若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
2.如图,在△ABC中,AD为高,AE平分∠BAC,∠B=50°,∠C=80°,则∠DAE的度数为( )
A.15° B.20° C.25° D.30°
3.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )
A.125° B.130° C.135° D.140°
4.下列条件中,能构成钝角△ABC的是( )
A.∠A=∠B=∠C B.∠A+∠C=∠B
C.∠B=∠C=∠A D.∠A=∠B=∠C
5.如果一个三角形有两个角分别为80°,50°,则这个三角形是( )三角形.
A.等腰 B.等边 C.不等边 D.直角
6.在△ABC中,若∠A=40°,∠B=100°,则∠C=( )
A.70° B.60° C.50° D.40°
7.如图,在△ABC中,∠B=38°,∠C=54°,AE是BC边上的高,AD是∠BAC的平分线,则∠DAE的度数为( )
A.8° B.10° C.12° D.14°
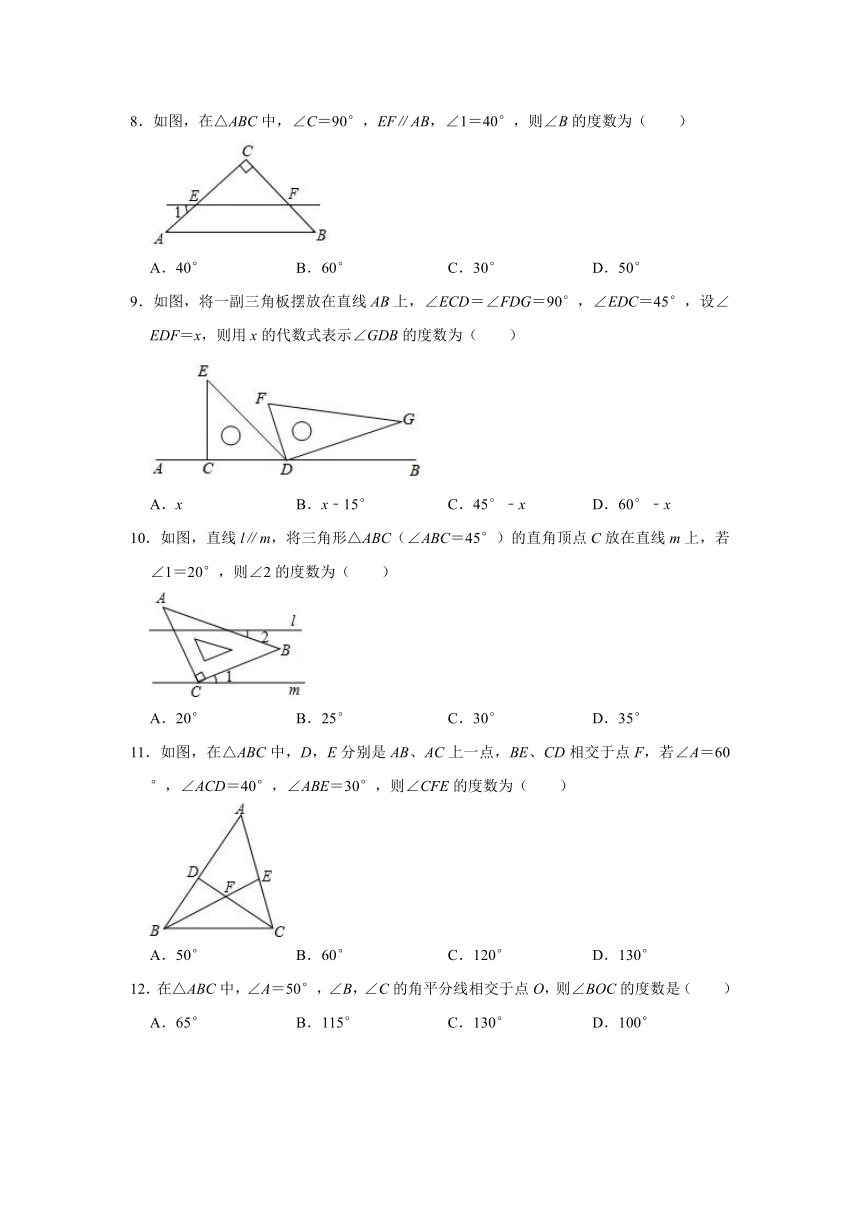
8.如图,在△ABC中,∠C=90°,EF∥AB,∠1=40°,则∠B的度数为( )
A.40° B.60° C.30° D.50°
9.如图,将一副三角板摆放在直线AB上,∠ECD=∠FDG=90°,∠EDC=45°,设∠EDF=x,则用x的代数式表示∠GDB的度数为( )
A.x B.x﹣15° C.45°﹣x D.60°﹣x
10.如图,直线l∥m,将三角形△ABC(∠ABC=45°)的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
11.如图,在△ABC中,D,E分别是AB、AC上一点,BE、CD相交于点F,若∠A=60°,∠ACD=40°,∠ABE=30°,则∠CFE的度数为( )
A.50° B.60° C.120° D.130°
12.在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC的度数是( )
A.65° B.115° C.130° D.100°
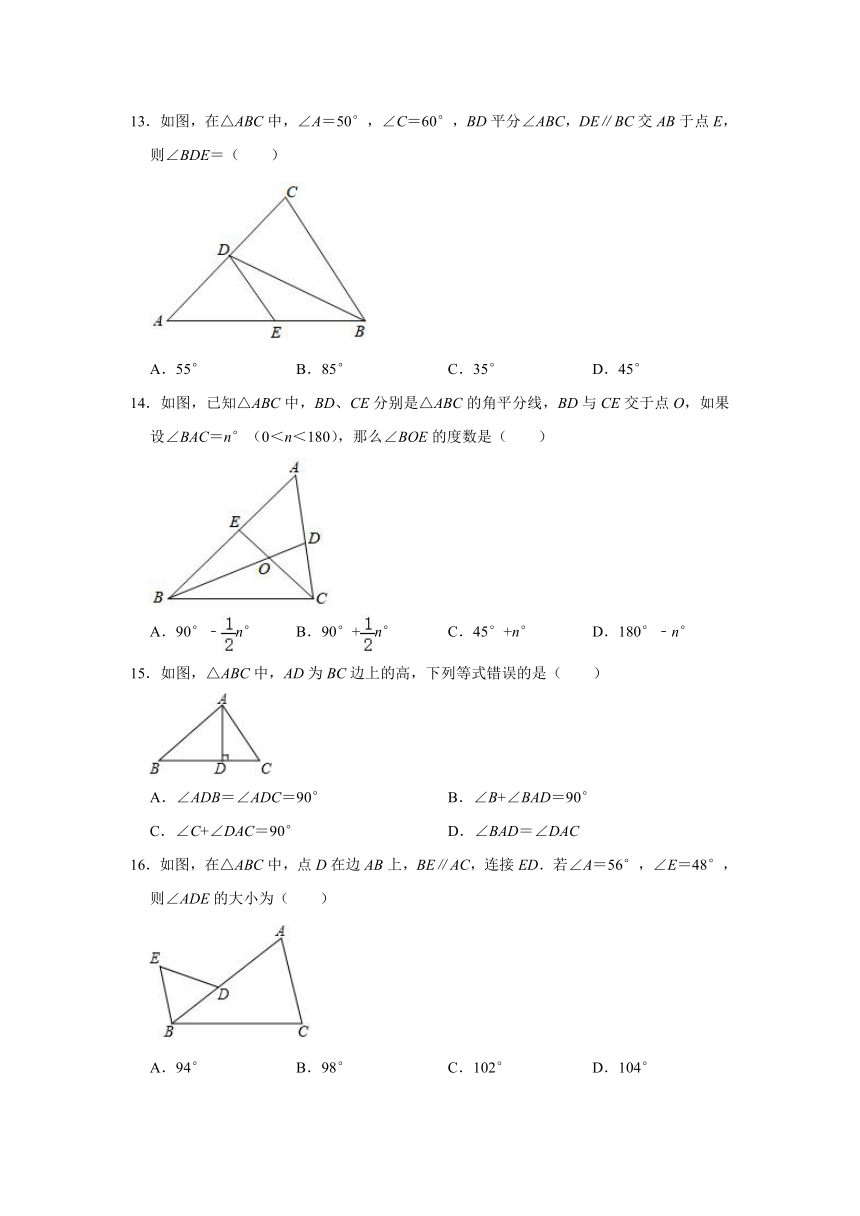
13.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,DE∥BC交AB于点E,则∠BDE=( )
A.55° B.85° C.35° D.45°
14.如图,已知△ABC中,BD、CE分别是△ABC的角平分线,BD与CE交于点O,如果设∠BAC=n°(0<n<180),那么∠BOE的度数是( )
A.90°﹣n° B.90°+n° C.45°+n° D.180°﹣n°
15.如图,△ABC中,AD为BC边上的高,下列等式错误的是( )
A.∠ADB=∠ADC=90° B.∠B+∠BAD=90°
C.∠C+∠DAC=90° D.∠BAD=∠DAC
16.如图,在△ABC中,点D在边AB上,BE∥AC,连接ED.若∠A=56°,∠E=48°,则∠ADE的大小为( )
A.94° B.98° C.102° D.104°
17.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10° B.30° C.65° D.85°
18.如图,在△ABC中,DF∥AB交AC于点E,交BC于点F,连接DC,∠A=70°,∠D=38°,则∠DCA的度数是( )
A.42° B.38° C.40° D.32°
19.已知△ABC的三个内角的大小关系为∠A﹣∠B=∠C,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
20.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
21.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10° B.12° C.14° D.16°
22.在△ABC中,∠A:∠B:∠C=1:1:4,则∠A=( )
A.30° B.45° C.90° D.120°
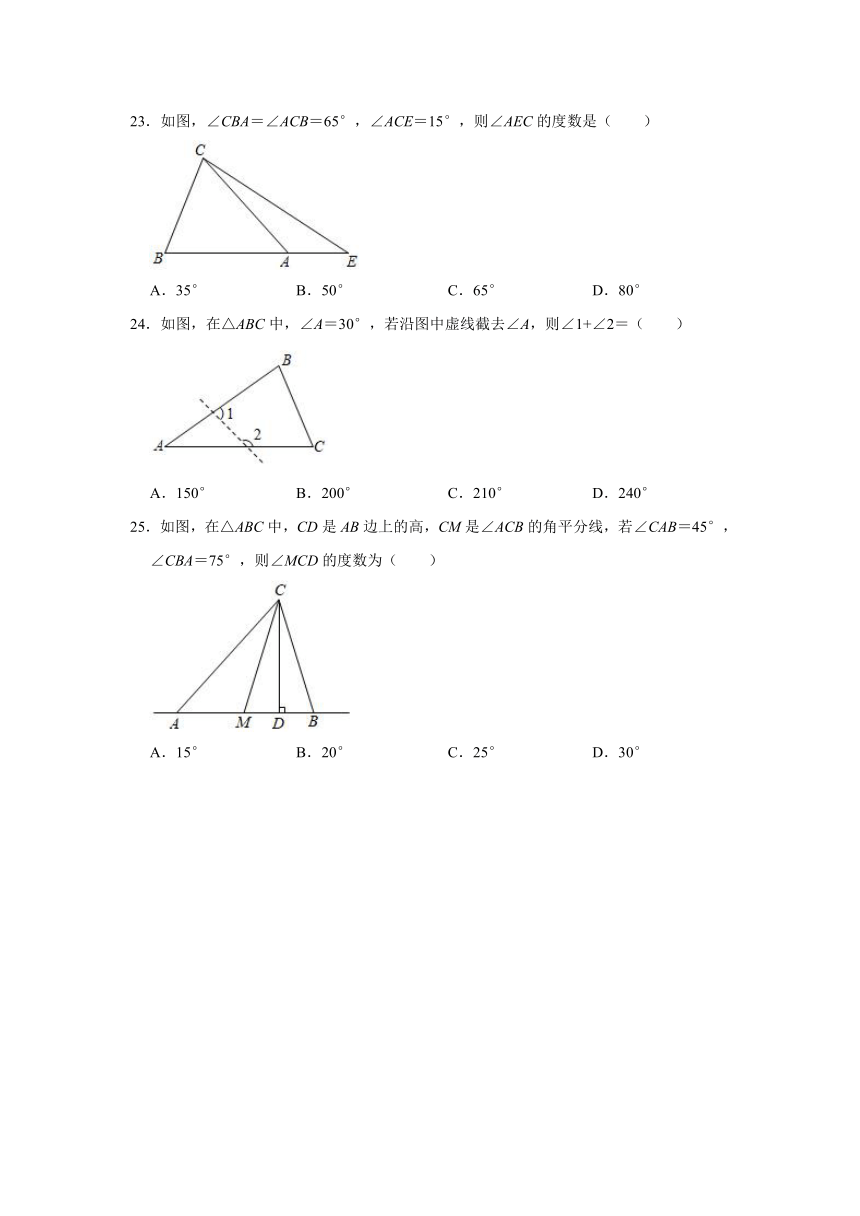
23.如图,∠CBA=∠ACB=65°,∠ACE=15°,则∠AEC的度数是( )
A.35° B.50° C.65° D.80°
24.如图,在△ABC中,∠A=30°,若沿图中虚线截去∠A,则∠1+∠2=( )
A.150° B.200° C.210° D.240°
25.如图,在△ABC中,CD是AB边上的高,CM是∠ACB的角平分线,若∠CAB=45°,∠CBA=75°,则∠MCD的度数为( )
A.15° B.20° C.25° D.30°
参考答案
1.解:设三角形三个内角度数分别为3份,4份,5份,
180°÷(3+4+5)
=180°÷12
=15°,
15°×5=75°,
这个三角形最大的角是75°,是锐角,所以这个三角形是锐角三角形.
故选:A.
2.解:∵在△ABC中,AD是高,∠B=50°,∠C=80°,
∴∠ADC=90°,∠BAC=180°﹣∠B﹣∠C=50°,
∴∠CAD=10°,
∵AE平分∠BAC,
∴∠CAE=25°,
∴∠DAE=∠CAE﹣∠CAD=15°,
故选:A.
3.解:∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:A.
4.解:A.根据三角形内角和定理,由∠A=∠B=∠C,得∠A=∠B=∠C=60°,故△ABC是锐角三角形,那么A不符合题意.
B.根据三角形内角和定理,由∠A+∠B+∠C=180°,得2∠B=180°,故∠B=90°,即△ABC是直角三角形,那么B不符合题意.
C.根据三角形内角和定理,由∠A+∠B+∠C=180°,∠B=∠C=∠A,得∠A+=180°,故∠A=120°,此时△ABC是钝角三角形,那么C符合题意.
D.根据三角形内角和定理,由∠A+∠B+∠C=180°,∠A=∠B=∠C,得∠A=30°,∠B=60°,∠C=90°,此时△ABC是直角三角形,那么D不符合题意.
故选:C.
5.解:第三个角=180°﹣80°﹣50°=50°,
故这个三角形是等腰三角形.
故选:A.
6.解:在△ABC中,∵∠A=40°,∠B=100°,
∴∠C=180°﹣∠A﹣∠B=40°,
故选:D.
7.解:在△ABC中,∵∠B=38°,∠C=54°,
∴∠BAC=180°﹣∠B﹣∠C=88°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=44°,
∵AE是BC边上的高,
∴∠AEC=90°,
在△AEC中,∠AEC=90°,∠C=54°,
∴∠EAC=180°﹣∠AEC﹣∠C=36°,
∴∠DAE=∠DAC﹣∠EAC=8°.
故选:A.
8.解:∵∠2+∠3=90°,∠2=∠1=40°,
∴∠3=50°.
∵EF∥AB,
∠B=∠3=50°.
故选:D.
9.解:∵∠FDG=90°,∠EDC=45°,∠EDF=x,
∴∠GDB=180°﹣∠CDE﹣∠EDF﹣∠FDG
=180°﹣45°﹣x﹣90°
=45°﹣x,
故选:C.
10.解:过点B作直线n∥l.
∵l∥m,
∴m∥n∥l.
∴∠3=∠2,∠1=∠4.
∵∠ABC=45°,∠1=20°,
∴∠3=∠ABC﹣∠4
=45°﹣20°
=25°.
∴∠2=25°.
故选:B.
11.解:∵∠A=60°,∠ABE=30°,∠BEC为△ABE的外角,
∴∠BEC=∠A+∠ABE=90°,
∵∠ACD=40°,
根据三角形内角和定理可得,
∠CFE=180°﹣∠ACD﹣∠BEC=50°.
故选:A.
12.解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠B,∠C的角平分线相交于点O,
∴∠EBC=,,
∴∠EBC+∠DCB=65°,
∴∠BOC=115°,
故选:B.
13.解:在△ABC中,∠A=50°,∠C=60°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣50°﹣60°=70°,
∵BD平分∠ABC,
∴∠CBD=35°,
∵DE∥BC,
∴∠BDE=∠CBD=35°.
故选:C.
14.解:∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵BD、CE分别是△ABC的角平分线,
∴∠OBC+∠OCB==90°﹣n°,
∴∠BOE=∠OBC+∠OCB=90°﹣n°,
故选:A.
15.解:∵AD为BC边上的高
∴∠ADB=∠ADC=90°
∴∠B+∠BAD=90°,∠C+∠DAC=90°,
∴A,B,C选项正确,
∵∠BAD与∠DAC不一定相等,
∴D选项错误,
故选:D.
16.解:∵BE∥AC,∠A=56°,
∴∠ABE=∠A=56°,
∵∠E=48°,
∴∠ADE=∠ABE+∠E=56°+48°=104°.
故选:D.
17.解:∵折叠后点A落在边CB上A′处,∠ACB=90°
∴折痕CD是角平分线,
∴∠A′CD=∠ACD=45°
又∵∠A=50°,
∴∠A′DC=∠ADC=180°﹣∠A﹣∠ACD=180°﹣50°﹣45°=85°.
故选:D.
18.解:∵DF∥AB,∠A=70°
∴∠A=∠FEC=70°.
∵∠FEC=∠D+∠DCA,∠D=38°,
∴∠DCA=∠FEC﹣∠D
=70°﹣38°
=32°.
故选:D.
19.解:∵∠A﹣∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=∠B+∠C,
即2∠A=180°,∠A=90°.
∴△ABC为直角三角形,
故选:B.
20.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
21.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
22.解:∵∠A:∠B:∠C=1:1:4且∠A+∠B+∠C=180°,
∴∠A==30°.
故选:A.
23.解:∵∠CBA=∠ACB=65°,
∴∠BAC=180°﹣∠CBA﹣∠ACB=180°﹣65°﹣65°=50°,
∴∠EAC=130°,
∵∠ACE=15°,
∴∠AEC=35°,
故选:A.
24.解:如图:∠1+∠3=180°,∠2+∠4=180°,
∴∠1+∠2+∠3+∠4=360°,
∵∠A+∠3+∠4=180°,∠A=30°,
∴∠3+∠4=150°,
∴∠1+∠2=210°.
故选:C.
25.解:∵∠CAB=45°,∠CBA=75°,
∴∠ACB=180°﹣∠CAB﹣∠CBA=60°.
∵CM是∠ACB的角平分线,
∴∠ACM=∠ACB=30°.
∴∠CMB=∠CAB+∠ACM=75°.
∵CD是AB边上的高,
∴∠CDA=∠CDB=90°.
∵∠CDB=∠MCD+∠CMB.
∴∠MCD=∠CDB﹣∠CMB
=90°﹣75°
=15°.
故选:A.
1.若一个三角形三个内角度数的比为3:4:5,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.等边三角形 D.钝角三角形
2.如图,在△ABC中,AD为高,AE平分∠BAC,∠B=50°,∠C=80°,则∠DAE的度数为( )
A.15° B.20° C.25° D.30°
3.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠A=70°,则∠BOC的度数为( )
A.125° B.130° C.135° D.140°
4.下列条件中,能构成钝角△ABC的是( )
A.∠A=∠B=∠C B.∠A+∠C=∠B
C.∠B=∠C=∠A D.∠A=∠B=∠C
5.如果一个三角形有两个角分别为80°,50°,则这个三角形是( )三角形.
A.等腰 B.等边 C.不等边 D.直角
6.在△ABC中,若∠A=40°,∠B=100°,则∠C=( )
A.70° B.60° C.50° D.40°
7.如图,在△ABC中,∠B=38°,∠C=54°,AE是BC边上的高,AD是∠BAC的平分线,则∠DAE的度数为( )
A.8° B.10° C.12° D.14°
8.如图,在△ABC中,∠C=90°,EF∥AB,∠1=40°,则∠B的度数为( )
A.40° B.60° C.30° D.50°
9.如图,将一副三角板摆放在直线AB上,∠ECD=∠FDG=90°,∠EDC=45°,设∠EDF=x,则用x的代数式表示∠GDB的度数为( )
A.x B.x﹣15° C.45°﹣x D.60°﹣x
10.如图,直线l∥m,将三角形△ABC(∠ABC=45°)的直角顶点C放在直线m上,若∠1=20°,则∠2的度数为( )
A.20° B.25° C.30° D.35°
11.如图,在△ABC中,D,E分别是AB、AC上一点,BE、CD相交于点F,若∠A=60°,∠ACD=40°,∠ABE=30°,则∠CFE的度数为( )
A.50° B.60° C.120° D.130°
12.在△ABC中,∠A=50°,∠B,∠C的角平分线相交于点O,则∠BOC的度数是( )
A.65° B.115° C.130° D.100°
13.如图,在△ABC中,∠A=50°,∠C=60°,BD平分∠ABC,DE∥BC交AB于点E,则∠BDE=( )
A.55° B.85° C.35° D.45°
14.如图,已知△ABC中,BD、CE分别是△ABC的角平分线,BD与CE交于点O,如果设∠BAC=n°(0<n<180),那么∠BOE的度数是( )
A.90°﹣n° B.90°+n° C.45°+n° D.180°﹣n°
15.如图,△ABC中,AD为BC边上的高,下列等式错误的是( )
A.∠ADB=∠ADC=90° B.∠B+∠BAD=90°
C.∠C+∠DAC=90° D.∠BAD=∠DAC
16.如图,在△ABC中,点D在边AB上,BE∥AC,连接ED.若∠A=56°,∠E=48°,则∠ADE的大小为( )
A.94° B.98° C.102° D.104°
17.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠使点A落在BC边上的点A′处,折痕为CD,则∠A′DC=( )
A.10° B.30° C.65° D.85°
18.如图,在△ABC中,DF∥AB交AC于点E,交BC于点F,连接DC,∠A=70°,∠D=38°,则∠DCA的度数是( )
A.42° B.38° C.40° D.32°
19.已知△ABC的三个内角的大小关系为∠A﹣∠B=∠C,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
20.已知△ABC中,∠A:∠B:∠C=3:4:7,则△ABC一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
21.如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=48°,∠C=68°,则∠DAE的度数是( )
A.10° B.12° C.14° D.16°
22.在△ABC中,∠A:∠B:∠C=1:1:4,则∠A=( )
A.30° B.45° C.90° D.120°
23.如图,∠CBA=∠ACB=65°,∠ACE=15°,则∠AEC的度数是( )
A.35° B.50° C.65° D.80°
24.如图,在△ABC中,∠A=30°,若沿图中虚线截去∠A,则∠1+∠2=( )
A.150° B.200° C.210° D.240°
25.如图,在△ABC中,CD是AB边上的高,CM是∠ACB的角平分线,若∠CAB=45°,∠CBA=75°,则∠MCD的度数为( )
A.15° B.20° C.25° D.30°
参考答案
1.解:设三角形三个内角度数分别为3份,4份,5份,
180°÷(3+4+5)
=180°÷12
=15°,
15°×5=75°,
这个三角形最大的角是75°,是锐角,所以这个三角形是锐角三角形.
故选:A.
2.解:∵在△ABC中,AD是高,∠B=50°,∠C=80°,
∴∠ADC=90°,∠BAC=180°﹣∠B﹣∠C=50°,
∴∠CAD=10°,
∵AE平分∠BAC,
∴∠CAE=25°,
∴∠DAE=∠CAE﹣∠CAD=15°,
故选:A.
3.解:∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∵BO、CO分别是∠ABC、∠ACB的平分线,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°.
故选:A.
4.解:A.根据三角形内角和定理,由∠A=∠B=∠C,得∠A=∠B=∠C=60°,故△ABC是锐角三角形,那么A不符合题意.
B.根据三角形内角和定理,由∠A+∠B+∠C=180°,得2∠B=180°,故∠B=90°,即△ABC是直角三角形,那么B不符合题意.
C.根据三角形内角和定理,由∠A+∠B+∠C=180°,∠B=∠C=∠A,得∠A+=180°,故∠A=120°,此时△ABC是钝角三角形,那么C符合题意.
D.根据三角形内角和定理,由∠A+∠B+∠C=180°,∠A=∠B=∠C,得∠A=30°,∠B=60°,∠C=90°,此时△ABC是直角三角形,那么D不符合题意.
故选:C.
5.解:第三个角=180°﹣80°﹣50°=50°,
故这个三角形是等腰三角形.
故选:A.
6.解:在△ABC中,∵∠A=40°,∠B=100°,
∴∠C=180°﹣∠A﹣∠B=40°,
故选:D.
7.解:在△ABC中,∵∠B=38°,∠C=54°,
∴∠BAC=180°﹣∠B﹣∠C=88°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=44°,
∵AE是BC边上的高,
∴∠AEC=90°,
在△AEC中,∠AEC=90°,∠C=54°,
∴∠EAC=180°﹣∠AEC﹣∠C=36°,
∴∠DAE=∠DAC﹣∠EAC=8°.
故选:A.
8.解:∵∠2+∠3=90°,∠2=∠1=40°,
∴∠3=50°.
∵EF∥AB,
∠B=∠3=50°.
故选:D.
9.解:∵∠FDG=90°,∠EDC=45°,∠EDF=x,
∴∠GDB=180°﹣∠CDE﹣∠EDF﹣∠FDG
=180°﹣45°﹣x﹣90°
=45°﹣x,
故选:C.
10.解:过点B作直线n∥l.
∵l∥m,
∴m∥n∥l.
∴∠3=∠2,∠1=∠4.
∵∠ABC=45°,∠1=20°,
∴∠3=∠ABC﹣∠4
=45°﹣20°
=25°.
∴∠2=25°.
故选:B.
11.解:∵∠A=60°,∠ABE=30°,∠BEC为△ABE的外角,
∴∠BEC=∠A+∠ABE=90°,
∵∠ACD=40°,
根据三角形内角和定理可得,
∠CFE=180°﹣∠ACD﹣∠BEC=50°.
故选:A.
12.解:∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵∠B,∠C的角平分线相交于点O,
∴∠EBC=,,
∴∠EBC+∠DCB=65°,
∴∠BOC=115°,
故选:B.
13.解:在△ABC中,∠A=50°,∠C=60°,
∴∠ABC=180°﹣∠A﹣∠C=180°﹣50°﹣60°=70°,
∵BD平分∠ABC,
∴∠CBD=35°,
∵DE∥BC,
∴∠BDE=∠CBD=35°.
故选:C.
14.解:∵∠BAC=n°,
∴∠ABC+∠ACB=(180﹣n)°,
∵BD、CE分别是△ABC的角平分线,
∴∠OBC+∠OCB==90°﹣n°,
∴∠BOE=∠OBC+∠OCB=90°﹣n°,
故选:A.
15.解:∵AD为BC边上的高
∴∠ADB=∠ADC=90°
∴∠B+∠BAD=90°,∠C+∠DAC=90°,
∴A,B,C选项正确,
∵∠BAD与∠DAC不一定相等,
∴D选项错误,
故选:D.
16.解:∵BE∥AC,∠A=56°,
∴∠ABE=∠A=56°,
∵∠E=48°,
∴∠ADE=∠ABE+∠E=56°+48°=104°.
故选:D.
17.解:∵折叠后点A落在边CB上A′处,∠ACB=90°
∴折痕CD是角平分线,
∴∠A′CD=∠ACD=45°
又∵∠A=50°,
∴∠A′DC=∠ADC=180°﹣∠A﹣∠ACD=180°﹣50°﹣45°=85°.
故选:D.
18.解:∵DF∥AB,∠A=70°
∴∠A=∠FEC=70°.
∵∠FEC=∠D+∠DCA,∠D=38°,
∴∠DCA=∠FEC﹣∠D
=70°﹣38°
=32°.
故选:D.
19.解:∵∠A﹣∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=∠B+∠C,
即2∠A=180°,∠A=90°.
∴△ABC为直角三角形,
故选:B.
20.解:由题意可设∠A=3x,∠B=4x,∠C=7x.
∵∠A+∠B+∠C=180°,
∴3x+4x+7x=180°.
∴x=()°.
∴7x=90°.
∴△ABC是直角三角形.
故选:B.
21.解:∵∠B=48°,∠C=68°,
∴∠BAC=180°﹣∠B﹣∠C=64°,
∵AE平分∠BAC,
∴∠EAC=BAC=32°,
∵AD是△ABC的BC边上的高,
∴∠ADC=90°,
∵∠C=68°,
∴∠DAC=90°﹣∠C=22°,
∴∠DAE=∠EAC﹣∠DAC=32°﹣22°=10°,
故选:A.
22.解:∵∠A:∠B:∠C=1:1:4且∠A+∠B+∠C=180°,
∴∠A==30°.
故选:A.
23.解:∵∠CBA=∠ACB=65°,
∴∠BAC=180°﹣∠CBA﹣∠ACB=180°﹣65°﹣65°=50°,
∴∠EAC=130°,
∵∠ACE=15°,
∴∠AEC=35°,
故选:A.
24.解:如图:∠1+∠3=180°,∠2+∠4=180°,
∴∠1+∠2+∠3+∠4=360°,
∵∠A+∠3+∠4=180°,∠A=30°,
∴∠3+∠4=150°,
∴∠1+∠2=210°.
故选:C.
25.解:∵∠CAB=45°,∠CBA=75°,
∴∠ACB=180°﹣∠CAB﹣∠CBA=60°.
∵CM是∠ACB的角平分线,
∴∠ACM=∠ACB=30°.
∴∠CMB=∠CAB+∠ACM=75°.
∵CD是AB边上的高,
∴∠CDA=∠CDB=90°.
∵∠CDB=∠MCD+∠CMB.
∴∠MCD=∠CDB﹣∠CMB
=90°﹣75°
=15°.
故选:A.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
