2021-2022学年冀教版九年级数学下册29.3切线的性质与判定同步练习题(word解析版)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册29.3切线的性质与判定同步练习题(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 12:03:15 | ||
图片预览


文档简介
2021-2022学年冀教版九年级数学下册《29.3切线的性质与判定》同步练习题(附答案)
1.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A. B. C.5 D.
2.如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
3.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
4.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
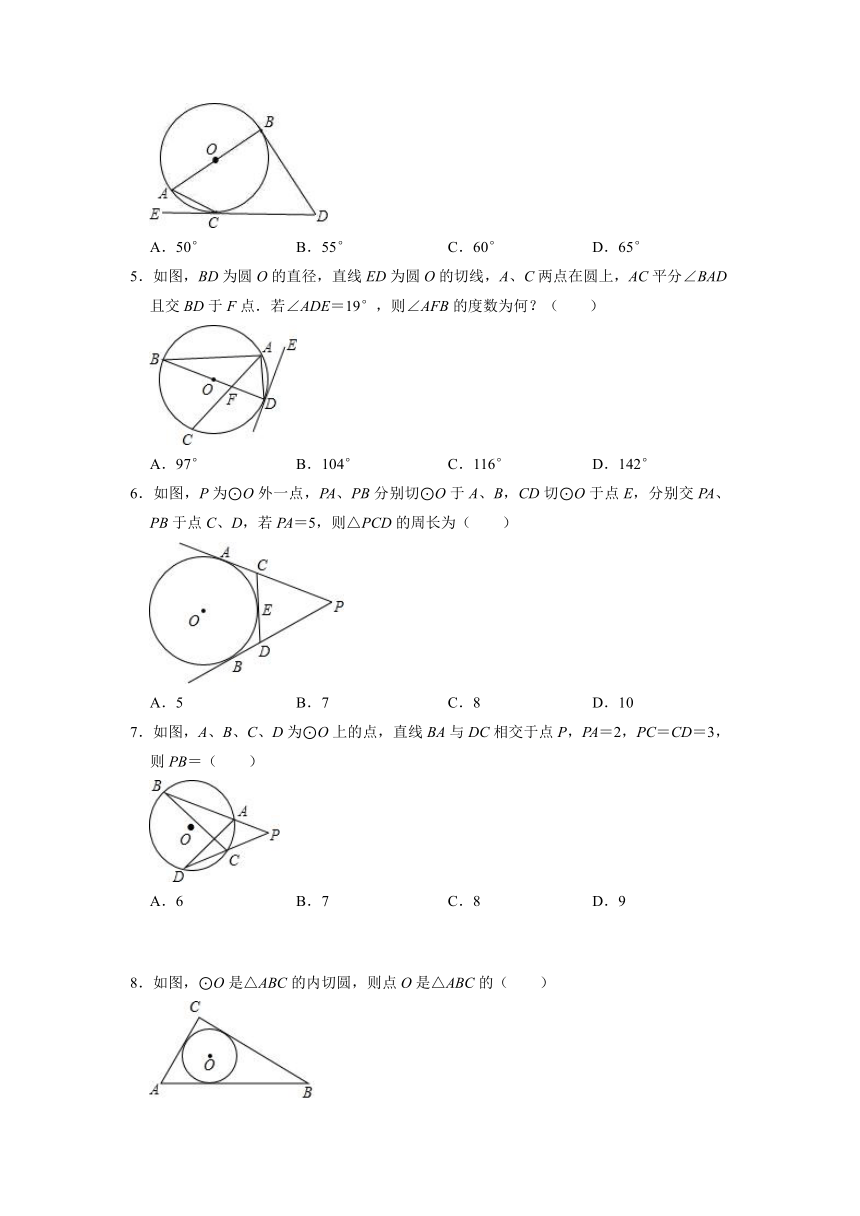
A.50° B.55° C.60° D.65°
5.如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?( )
A.97° B.104° C.116° D.142°
6.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5 B.7 C.8 D.10
7.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( )
A.6 B.7 C.8 D.9
8.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
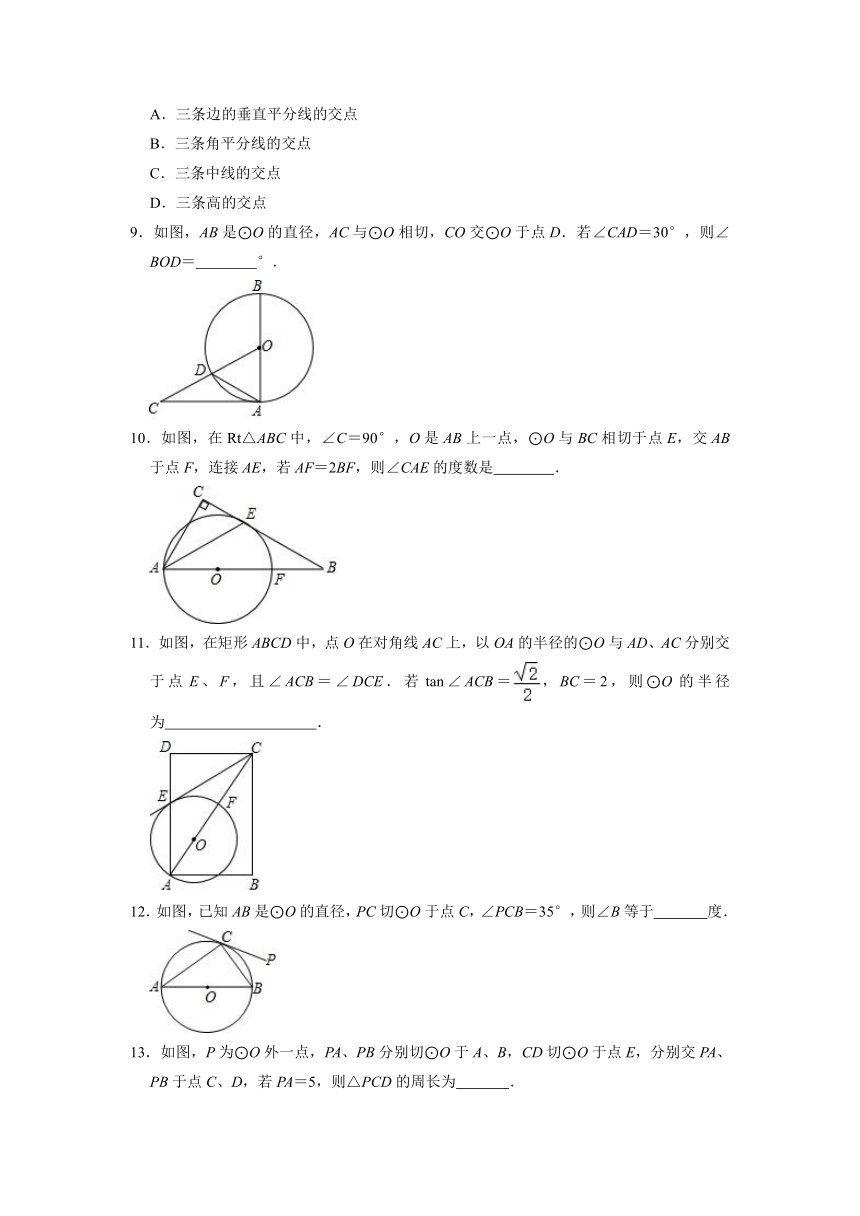
9.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD= °.
10.如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是 .
11.如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=,BC=2,则⊙O的半径为 .
12.如图,已知AB是⊙O的直径,PC切⊙O于点C,∠PCB=35°,则∠B等于 度.
13.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为 .
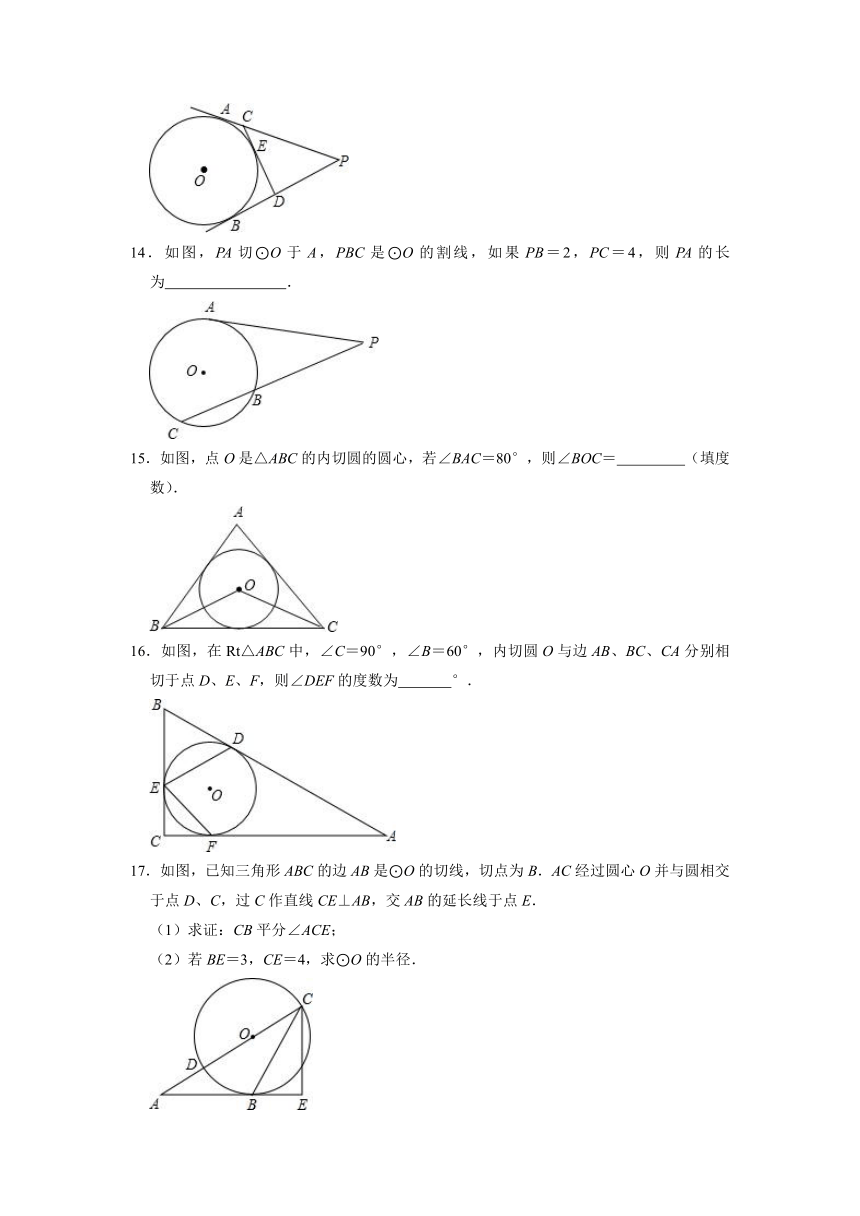
14.如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为 .
15.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC= (填度数).
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
17.如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
18.如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
19.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
20.(1)如图(1),△ABC内接于⊙O,AB为直径,∠CAE=∠B,试说明AE与⊙O相切于点A.
(2)在图(2)中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗?请说明理由.
21.如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
22.如图,PA为圆的切线,A为切点,PBC为割线,∠APC的平分线交AB于点D,交AC于点E.
求证:(1)AD=AE;(2)AB AE=AC DB.
23.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
24.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若,求BD的长.
25.如图,∠C=90°,⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,连接OE,OF.AO的延长线交BC于点D,AC=6,CD=2.
(1)求证:四边形OECF为正方形;
(2)求⊙O的半径;
(3)求AB的长.
26.如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O的半径和BF的长.
参考答案
1.解:方法1、过点O作OD⊥AC于点D,
∵AB是⊙O的直径,PA切⊙O于点A,
∴AB⊥AP,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠AOC=120°,
∵OA=OC,
∴∠OAD=30°,
∵AB=10,
∴OA=5,
∴OD=AO=2.5,
∴AD==,
∴AC=2AD=5,
故选A,
方法2、如图,
连接BC,∵AP是⊙O的切线,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠BOC=60°,
∴∠ACP=∠BAC=∠BOC=30°=∠P,
∴AP=AC,
∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ABC中,∠BAC=30°,AB=10,
∴AC=5,
故选:A.
2.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴与不能确定相等,所以③错误;
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为⊙O的切线,所以④正确.
故选:D.
3.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
4.
解:连接BC,
∵DB、DE分别切⊙O于点B、C,
∴BD=DC,
∵∠ACE=25°,
∴∠ABC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DBC=∠DCB=90°﹣25°=65°,
∴∠D=50°.
解法二:连接OC,BC.
∵DB,DC是⊙O的切线,B,C是切点,
∴∠OCE=∠OBD=90°,BD=DC,
∵OA=OC,
∴∠A=∠OCA,
∵AB是直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,∠OCA+∠ACE=90°,
∴∠ACE=∠ABC=25°,
∴∠BDC=∠DCB=90°﹣25°=65°,
∴∠D=180°﹣2×65°=50°,
故选:A.
5.解:∵BD是圆O的直径,
∴∠BAD=90°,
又∵AC平分∠BAD,
∴∠BAF=∠DAF=45°,
∵直线ED为圆O的切线,
∴∠ADE=∠ABD=19°,
∴∠AFB=180°﹣∠BAF﹣∠ABD=180°﹣45°﹣19°=116°.
故选:C.
6.解:∵PA、PB为圆的两条相交切线,
∴PA=PB,
同理可得:CA=CE,DE=DB.
∵△PCD的周长=PC+CE+ED+PD,
∴△PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
∴△PCD的周长=10,
故选:D.
7.解:∵PB,PD是⊙O的割线,
∴PA PB=PC PD,
∵PA=2,PC=CD=3,
∴2PB=3×6
解得:PB=9.
故选:D.
8.解:∵⊙O是△ABC的内切圆,
则点O到三边的距离相等,
∴点O是△ABC的三条角平分线的交点;
故选:B.
9.解:∵AC与⊙O相切,
∴∠BAC=90°,
∵∠CAD=30°,
∴∠OAD=60°,
∴∠BOD=2∠BAD=120°,
故答案为:120.
10.解:连接OE、EF,
∵⊙O与BC相切于点E,
∴OE⊥BC,
∵AF是直径,
∴∠AEF=90°,
∵OA=OF=AF,AF=2BF,
∴OF=BF,
∴OE=OF=EF,
∴∠OEF=60°,
∴∠AEO=90°﹣60°=30°,
∵AC⊥BC,OE⊥BC,
∴OE∥AC,
∴∠CAE=∠AEO=30°,
故答案为30°.
11.解:连接EF,
∵∠ACB=∠DCE,∠B=∠D=90°,
∴△ABC∽△EDC,
∴=,即=,
∵BC=2,
∴AB=CD=,
∴DE=1,
∴AE=DE,
∵AF为直径,
∴EF⊥AD,
∴EF∥CD,
∴AF=CF,
在Rt△ABC中,AB=,BC=2,
∴AC=,
∴⊙O的半径OA=AF=AC=.
故答案为:.
12.解:∵PC切⊙O于点C,∠PCB=35°,
∴∠A=∠PCB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∴35°+∠B=90°,
解得∠B=55°.
故答案为:55.
13.解:∵PA、PB切⊙O于A、B,
∴PA=PB=5;
同理,可得:EC=CA,DE=DB;
∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=PA+PB=2PA=10.
即△PCD的周长是10.
14.解:∵PA切⊙O于A,PBC是⊙O的割线,PB=2,PC=4,
∴PA2=PB×PC,
∴PA==2.
故答案为:2.
15.解:∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵点O是△ABC的内切圆的圆心,
∴BO,CO分别为∠ABC,∠BCA的角平分线,
∴∠OBC+∠OCB=50°,
∴∠BOC=130°.
故答案为:130°.
16.解:连接DO,FO,
∵在Rt△ABC中,∠C=90°,∠B=60°
∴∠A=30°,
∵内切圆O与边AB、BC、CA分别相切于点D、E、F,
∴∠ODA=∠OFA=90°,
∴∠DOF=150°,
∴∠DEF的度数为75°.
故答案为:75.
17.(1)证明:如图1,连接OB,
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE⊥AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图2,连接BD,
∵CE⊥AB,
∴∠E=90°,
∴BC===5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴,
∴BC2=CD CE,
∴CD==,
∴OC==,
∴⊙O的半径=.
18.(1)证明:连接OD.
∵AB与⊙O相切于点D,又AC与⊙O相切于点C,
∴AC=AD,OC⊥CA.
∴CF是⊙O的直径,
∵OC=OD,
∴OA⊥CD,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC==8,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵AB是切线,
∴OD⊥AB,
∴∠ODB=90°,
∵CF是直径,
∴∠CDF=90°,
∵∠BDF+∠ODF=90°,∠CDO+∠ODF=90°,
∴∠BDF=∠CDO,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠BDF=∠BCD,
∴△BDF∽△BCD,可得BD2=BF BC,
∴BF=2,
∴CF=BC﹣BF=6.OC=CF=3,
∴OA==3,
∵OC2=OE OA,
∴OE=,
∵EM∥AC,
∴===,
∴OM=,EM=,FM=OF+OM=,
∴===,
∴CG=EM=2.
19.(1)证明:连接OB,如图所示:
∵E是弦BD的中点,
∴BE=DE,OE⊥BD,=,
∴∠BOE=∠A,∠OBE+∠BOE=90°,
∵∠DBC=∠A,
∴∠BOE=∠DBC,
∴∠OBE+∠DBC=90°,
∴∠OBC=90°,
即BC⊥OB,
∴BC是⊙O的切线;
(2)解:∵OB=6,BC=8,BC⊥OB,
∴OC==10,
∵△OBC的面积=OC BE=OB BC,
∴BE===4.8,
∴BD=2BE=9.6,
即弦BD的长为9.6.
20.证明:(1)∵AB为直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
而∠CAE=∠B,
∴∠CAE+∠BAC=90°,即∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A;
(2)AE还与⊙O相切于点A.理由如下:
作直径AD,如图2,
∴∠D+∠DAC=90°,
∵∠B=∠D,
而∠CAE=∠B,
∴∠CAE+∠DAC=90°,即∠DAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
21.解:(1)证明:连接DO.
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中
∵OD=OB,OC=OC,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO.
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,
又∵点D在⊙O上,
∴CD是⊙O的切线;
(2)设⊙O的半径为R,则OD=R,OE=R+1,
∵CD是⊙O的切线,
∴∠EDO=90°,
∴ED2+OD2=OE2,
∴32+R2=(R+1)2,
解得R=4,
∴⊙O的半径为4.
22.证明:(1)∵∠ADE=∠APD+∠PAD,∠AED=∠CPE+∠C,
又∠APD=∠CPE,∠PAD=∠C.
∴∠ADE=∠AED.
∴AD=AE.
(2)∵∠APB=∠CPA,∠PAB=∠C,
∴△APB∽△CPA,得.
∵∠APE=∠BPD,∠AED=∠ADE=∠PDB,
∴△PBD∽△PEA,得.
∴.
∴AB AE=AC DB.
23.解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°;
(2)由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴BE+CG=BC=10cm.
(3)∵OF⊥BC,
∴S△OBC=OF×BC=OB×OC,即OF×10=×6×8.
∴OF=4.8cm.
24.(1)证明:连接OE,
∵BE平分∠ABC交AC于点E,
∴∠1=∠EBC,
∵∠1=∠2,
∴∠2=∠CBE,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线,
∵⊙O是△BDE的外接圆,
∴AC是△BDE的外接圆的切线;
(2)解:∵AE是圆O的切线,AB是圆的割线,
根据切割线定理:AE2=AD×AB,
∵,
∴()2=2×(2+BD),
解得:BD=4.
∴BD的长是:4.
25.(1)证明:∵⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,
∴∠C=∠CFO=∠CEO=90°,
∴四边形CFOE是矩形,
∵OF=OE,
∴四边形OECF为正方形;
(2)解:由题意可得:EO∥AC,
∴△DEO∽△DCA,
∴=,
设⊙O的半径为x,
则=,
解得:x=1.5,
故⊙O的半径为1.5;
(3)解:∵⊙O的半径为1.5,AC=6,
∴CF=1.5,AF=4.5
∴AG=4.5,
设BG=BE=y,
∴在Rt△ACB中
AC2+BC2=AB2,
∴62+(y+1.5)2=(4.5+y)2,
解得:y=3,
∴AB=AG+BG=4.5+3=7.5.
26.解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG=x,
∴DG=OE=2x,
根据AC=AB得:4x=x+2x+2﹣,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
OF=2÷=,
∴BF=﹣2,⊙O的半径为2.
1.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A. B. C.5 D.
2.如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③=;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
A.①② B.①②③ C.①④ D.①②④
3.如图,直线AB、CD相交于点O,∠AOD=30°,半径为1cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.4 B.8 C.4或6 D.4或8
4.如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是( )
A.50° B.55° C.60° D.65°
5.如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?( )
A.97° B.104° C.116° D.142°
6.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5 B.7 C.8 D.10
7.如图,A、B、C、D为⊙O上的点,直线BA与DC相交于点P,PA=2,PC=CD=3,则PB=( )
A.6 B.7 C.8 D.9
8.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条高的交点
9.如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD= °.
10.如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是 .
11.如图,在矩形ABCD中,点O在对角线AC上,以OA的半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.若tan∠ACB=,BC=2,则⊙O的半径为 .
12.如图,已知AB是⊙O的直径,PC切⊙O于点C,∠PCB=35°,则∠B等于 度.
13.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为 .
14.如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为 .
15.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC= (填度数).
16.如图,在Rt△ABC中,∠C=90°,∠B=60°,内切圆O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为 °.
17.如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
18.如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
(1)求证:DF∥AO;
(2)若AC=6,AB=10,求CG的长.
19.如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
20.(1)如图(1),△ABC内接于⊙O,AB为直径,∠CAE=∠B,试说明AE与⊙O相切于点A.
(2)在图(2)中,若AB为非直径的弦,∠CAE=∠B,AE还与⊙O相切于点A吗?请说明理由.
21.如图,已知AB为⊙O的直径,AD、BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA、CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若AE=1,ED=3,求⊙O的半径.
22.如图,PA为圆的切线,A为切点,PBC为割线,∠APC的平分线交AB于点D,交AC于点E.
求证:(1)AD=AE;(2)AB AE=AC DB.
23.如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
24.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
(1)求证:AC是△BDE的外接圆的切线;
(2)若,求BD的长.
25.如图,∠C=90°,⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,连接OE,OF.AO的延长线交BC于点D,AC=6,CD=2.
(1)求证:四边形OECF为正方形;
(2)求⊙O的半径;
(3)求AB的长.
26.如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O的半径和BF的长.
参考答案
1.解:方法1、过点O作OD⊥AC于点D,
∵AB是⊙O的直径,PA切⊙O于点A,
∴AB⊥AP,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠AOC=120°,
∵OA=OC,
∴∠OAD=30°,
∵AB=10,
∴OA=5,
∴OD=AO=2.5,
∴AD==,
∴AC=2AD=5,
故选A,
方法2、如图,
连接BC,∵AP是⊙O的切线,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠BOC=60°,
∴∠ACP=∠BAC=∠BOC=30°=∠P,
∴AP=AC,
∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ABC中,∠BAC=30°,AB=10,
∴AC=5,
故选:A.
2.解:∵AB为直径,
∴∠ADB=90°,
∴BD⊥AC,
而AB=CB,
∴AD=DC,所以①正确;
∵AB=CB,
∴∠1=∠2,
而CD=ED,
∴∠3=∠4,
∵CF∥AB,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4,
∴△CBA∽△CDE,所以②正确;
∵△ABC不能确定为直角三角形,
∴∠1不能确定等于45°,
∴与不能确定相等,所以③错误;
∵DA=DC=DE,
∴点E在以AC为直径的圆上,
∴∠AEC=90°,
∴CE⊥AE,
而CF∥AB,
∴AB⊥AE,
∴AE为⊙O的切线,所以④正确.
故选:D.
3.解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.∴P1E⊥CD
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2cm
又∵OP=6cm
∴P1P=4cm
∴圆P到达圆P1需要时间为:4÷1=4(秒)
∴⊙P与直线CD相切时,时间为4秒,
当点P在点O的右侧时,同法可得t=8秒
故选:D.
4.
解:连接BC,
∵DB、DE分别切⊙O于点B、C,
∴BD=DC,
∵∠ACE=25°,
∴∠ABC=25°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠DBC=∠DCB=90°﹣25°=65°,
∴∠D=50°.
解法二:连接OC,BC.
∵DB,DC是⊙O的切线,B,C是切点,
∴∠OCE=∠OBD=90°,BD=DC,
∵OA=OC,
∴∠A=∠OCA,
∵AB是直径,
∴∠ACB=90°,
∴∠A+∠ABC=90°,∠OCA+∠ACE=90°,
∴∠ACE=∠ABC=25°,
∴∠BDC=∠DCB=90°﹣25°=65°,
∴∠D=180°﹣2×65°=50°,
故选:A.
5.解:∵BD是圆O的直径,
∴∠BAD=90°,
又∵AC平分∠BAD,
∴∠BAF=∠DAF=45°,
∵直线ED为圆O的切线,
∴∠ADE=∠ABD=19°,
∴∠AFB=180°﹣∠BAF﹣∠ABD=180°﹣45°﹣19°=116°.
故选:C.
6.解:∵PA、PB为圆的两条相交切线,
∴PA=PB,
同理可得:CA=CE,DE=DB.
∵△PCD的周长=PC+CE+ED+PD,
∴△PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
∴△PCD的周长=10,
故选:D.
7.解:∵PB,PD是⊙O的割线,
∴PA PB=PC PD,
∵PA=2,PC=CD=3,
∴2PB=3×6
解得:PB=9.
故选:D.
8.解:∵⊙O是△ABC的内切圆,
则点O到三边的距离相等,
∴点O是△ABC的三条角平分线的交点;
故选:B.
9.解:∵AC与⊙O相切,
∴∠BAC=90°,
∵∠CAD=30°,
∴∠OAD=60°,
∴∠BOD=2∠BAD=120°,
故答案为:120.
10.解:连接OE、EF,
∵⊙O与BC相切于点E,
∴OE⊥BC,
∵AF是直径,
∴∠AEF=90°,
∵OA=OF=AF,AF=2BF,
∴OF=BF,
∴OE=OF=EF,
∴∠OEF=60°,
∴∠AEO=90°﹣60°=30°,
∵AC⊥BC,OE⊥BC,
∴OE∥AC,
∴∠CAE=∠AEO=30°,
故答案为30°.
11.解:连接EF,
∵∠ACB=∠DCE,∠B=∠D=90°,
∴△ABC∽△EDC,
∴=,即=,
∵BC=2,
∴AB=CD=,
∴DE=1,
∴AE=DE,
∵AF为直径,
∴EF⊥AD,
∴EF∥CD,
∴AF=CF,
在Rt△ABC中,AB=,BC=2,
∴AC=,
∴⊙O的半径OA=AF=AC=.
故答案为:.
12.解:∵PC切⊙O于点C,∠PCB=35°,
∴∠A=∠PCB=35°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∴35°+∠B=90°,
解得∠B=55°.
故答案为:55.
13.解:∵PA、PB切⊙O于A、B,
∴PA=PB=5;
同理,可得:EC=CA,DE=DB;
∴△PDC的周长=PC+CE+DE+DP=PC+AC+PD+DB=PA+PB=2PA=10.
即△PCD的周长是10.
14.解:∵PA切⊙O于A,PBC是⊙O的割线,PB=2,PC=4,
∴PA2=PB×PC,
∴PA==2.
故答案为:2.
15.解:∵∠BAC=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵点O是△ABC的内切圆的圆心,
∴BO,CO分别为∠ABC,∠BCA的角平分线,
∴∠OBC+∠OCB=50°,
∴∠BOC=130°.
故答案为:130°.
16.解:连接DO,FO,
∵在Rt△ABC中,∠C=90°,∠B=60°
∴∠A=30°,
∵内切圆O与边AB、BC、CA分别相切于点D、E、F,
∴∠ODA=∠OFA=90°,
∴∠DOF=150°,
∴∠DEF的度数为75°.
故答案为:75.
17.(1)证明:如图1,连接OB,
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE⊥AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图2,连接BD,
∵CE⊥AB,
∴∠E=90°,
∴BC===5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴,
∴BC2=CD CE,
∴CD==,
∴OC==,
∴⊙O的半径=.
18.(1)证明:连接OD.
∵AB与⊙O相切于点D,又AC与⊙O相切于点C,
∴AC=AD,OC⊥CA.
∴CF是⊙O的直径,
∵OC=OD,
∴OA⊥CD,
∵CF是直径,
∴∠CDF=90°,
∴DF⊥CD,
∴DF∥AO.
(2)过点作EM⊥OC于M,
∵AC=6,AB=10,
∴BC==8,
∴AD=AC=6,
∴BD=AB﹣AD=4,
∵AB是切线,
∴OD⊥AB,
∴∠ODB=90°,
∵CF是直径,
∴∠CDF=90°,
∵∠BDF+∠ODF=90°,∠CDO+∠ODF=90°,
∴∠BDF=∠CDO,
∵OC=OD,
∴∠ODC=∠OCD,
∴∠BDF=∠BCD,
∴△BDF∽△BCD,可得BD2=BF BC,
∴BF=2,
∴CF=BC﹣BF=6.OC=CF=3,
∴OA==3,
∵OC2=OE OA,
∴OE=,
∵EM∥AC,
∴===,
∴OM=,EM=,FM=OF+OM=,
∴===,
∴CG=EM=2.
19.(1)证明:连接OB,如图所示:
∵E是弦BD的中点,
∴BE=DE,OE⊥BD,=,
∴∠BOE=∠A,∠OBE+∠BOE=90°,
∵∠DBC=∠A,
∴∠BOE=∠DBC,
∴∠OBE+∠DBC=90°,
∴∠OBC=90°,
即BC⊥OB,
∴BC是⊙O的切线;
(2)解:∵OB=6,BC=8,BC⊥OB,
∴OC==10,
∵△OBC的面积=OC BE=OB BC,
∴BE===4.8,
∴BD=2BE=9.6,
即弦BD的长为9.6.
20.证明:(1)∵AB为直径,
∴∠ACB=90°,
∴∠B+∠BAC=90°,
而∠CAE=∠B,
∴∠CAE+∠BAC=90°,即∠BAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A;
(2)AE还与⊙O相切于点A.理由如下:
作直径AD,如图2,
∴∠D+∠DAC=90°,
∵∠B=∠D,
而∠CAE=∠B,
∴∠CAE+∠DAC=90°,即∠DAE=90°,
∴OA⊥AE,
∴AE与⊙O相切于点A.
21.解:(1)证明:连接DO.
∵AD∥OC,
∴∠DAO=∠COB,∠ADO=∠COD.
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠COD=∠COB.
在△COD和△COB中
∵OD=OB,OC=OC,
∴△COD≌△COB(SAS),
∴∠CDO=∠CBO.
∵BC是⊙O的切线,
∴∠CBO=90°,
∴∠CDO=90°,
又∵点D在⊙O上,
∴CD是⊙O的切线;
(2)设⊙O的半径为R,则OD=R,OE=R+1,
∵CD是⊙O的切线,
∴∠EDO=90°,
∴ED2+OD2=OE2,
∴32+R2=(R+1)2,
解得R=4,
∴⊙O的半径为4.
22.证明:(1)∵∠ADE=∠APD+∠PAD,∠AED=∠CPE+∠C,
又∠APD=∠CPE,∠PAD=∠C.
∴∠ADE=∠AED.
∴AD=AE.
(2)∵∠APB=∠CPA,∠PAB=∠C,
∴△APB∽△CPA,得.
∵∠APE=∠BPD,∠AED=∠ADE=∠PDB,
∴△PBD∽△PEA,得.
∴.
∴AB AE=AC DB.
23.解:(1)连接OF;根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG;
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°;
(2)由(1)知,∠BOC=90°.
∵OB=6cm,OC=8cm,
∴由勾股定理得到:BC==10cm,
∴BE+CG=BC=10cm.
(3)∵OF⊥BC,
∴S△OBC=OF×BC=OB×OC,即OF×10=×6×8.
∴OF=4.8cm.
24.(1)证明:连接OE,
∵BE平分∠ABC交AC于点E,
∴∠1=∠EBC,
∵∠1=∠2,
∴∠2=∠CBE,
∴∠AEO=∠C=90°,
∴AC是⊙O的切线,
∵⊙O是△BDE的外接圆,
∴AC是△BDE的外接圆的切线;
(2)解:∵AE是圆O的切线,AB是圆的割线,
根据切割线定理:AE2=AD×AB,
∵,
∴()2=2×(2+BD),
解得:BD=4.
∴BD的长是:4.
25.(1)证明:∵⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,
∴∠C=∠CFO=∠CEO=90°,
∴四边形CFOE是矩形,
∵OF=OE,
∴四边形OECF为正方形;
(2)解:由题意可得:EO∥AC,
∴△DEO∽△DCA,
∴=,
设⊙O的半径为x,
则=,
解得:x=1.5,
故⊙O的半径为1.5;
(3)解:∵⊙O的半径为1.5,AC=6,
∴CF=1.5,AF=4.5
∴AG=4.5,
设BG=BE=y,
∴在Rt△ACB中
AC2+BC2=AB2,
∴62+(y+1.5)2=(4.5+y)2,
解得:y=3,
∴AB=AG+BG=4.5+3=7.5.
26.解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG=x,
∴DG=OE=2x,
根据AC=AB得:4x=x+2x+2﹣,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
OF=2÷=,
∴BF=﹣2,⊙O的半径为2.
