2021-2022学年北师大版八年级数学下册3.2 图形的旋转(第1课时)同步测试卷(word版含简单答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册3.2 图形的旋转(第1课时)同步测试卷(word版含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 263.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 12:07:13 | ||
图片预览

文档简介
3.2 图形的旋转(第1课时)同步测试卷 2021-2022学年北师大版八年级数学下册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分)
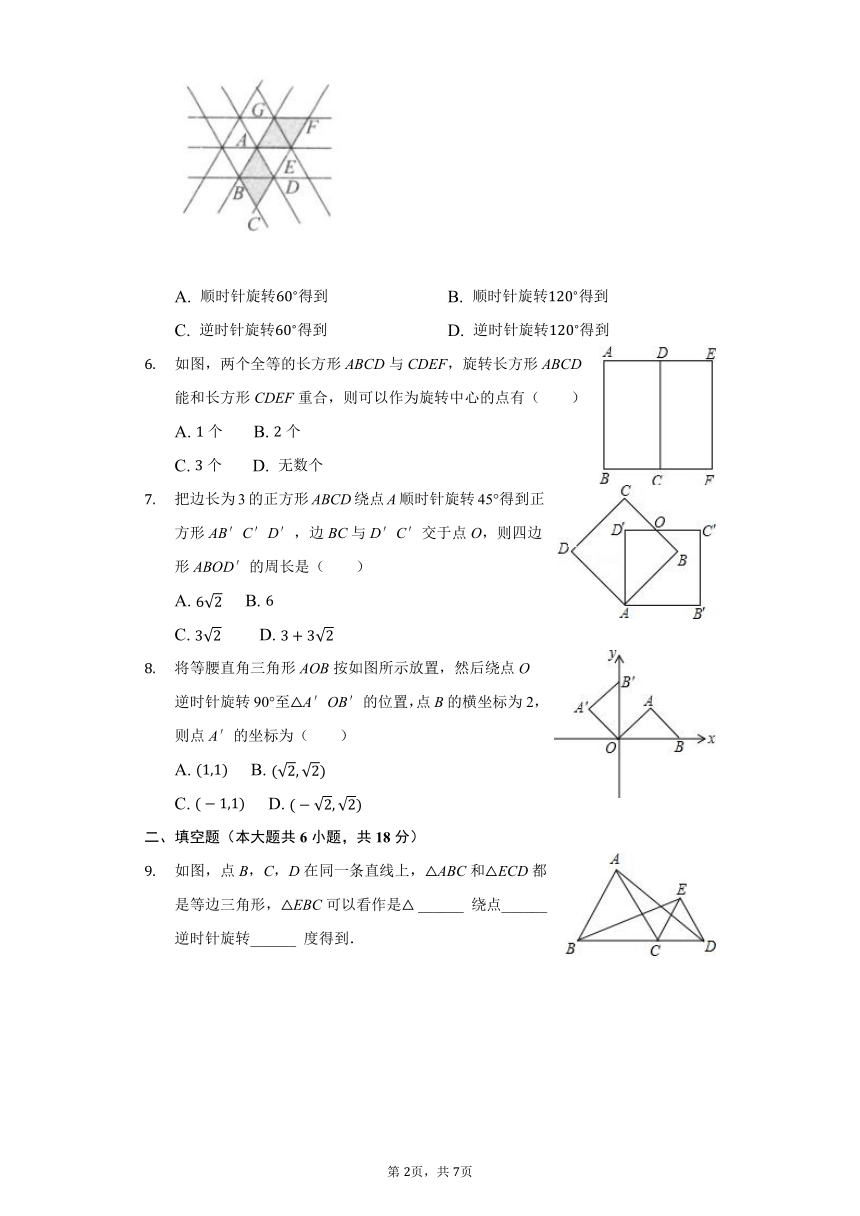
如图,将△ABC绕点P顺时针旋转90°得到△A’B’C’,则点P的坐标是(▲)
A. B.
C. D.
如图,在下面的四个三角形中,不能由ABC经过旋转或平移得到的是( )
A. B.
C. D.
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
如图,△ABD 经过旋转后到达△ ACE 的位置,下列说法不正确的是().
A. 点是旋转中心 B. 是一个旋转角
C. D. ≌
同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图看到的是万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的平行四边形AEFG可以看成是把平行四边形ABCD以A为中心( )
A. 顺时针旋转得到 B. 顺时针旋转得到
C. 逆时针旋转得到 D. 逆时针旋转得到
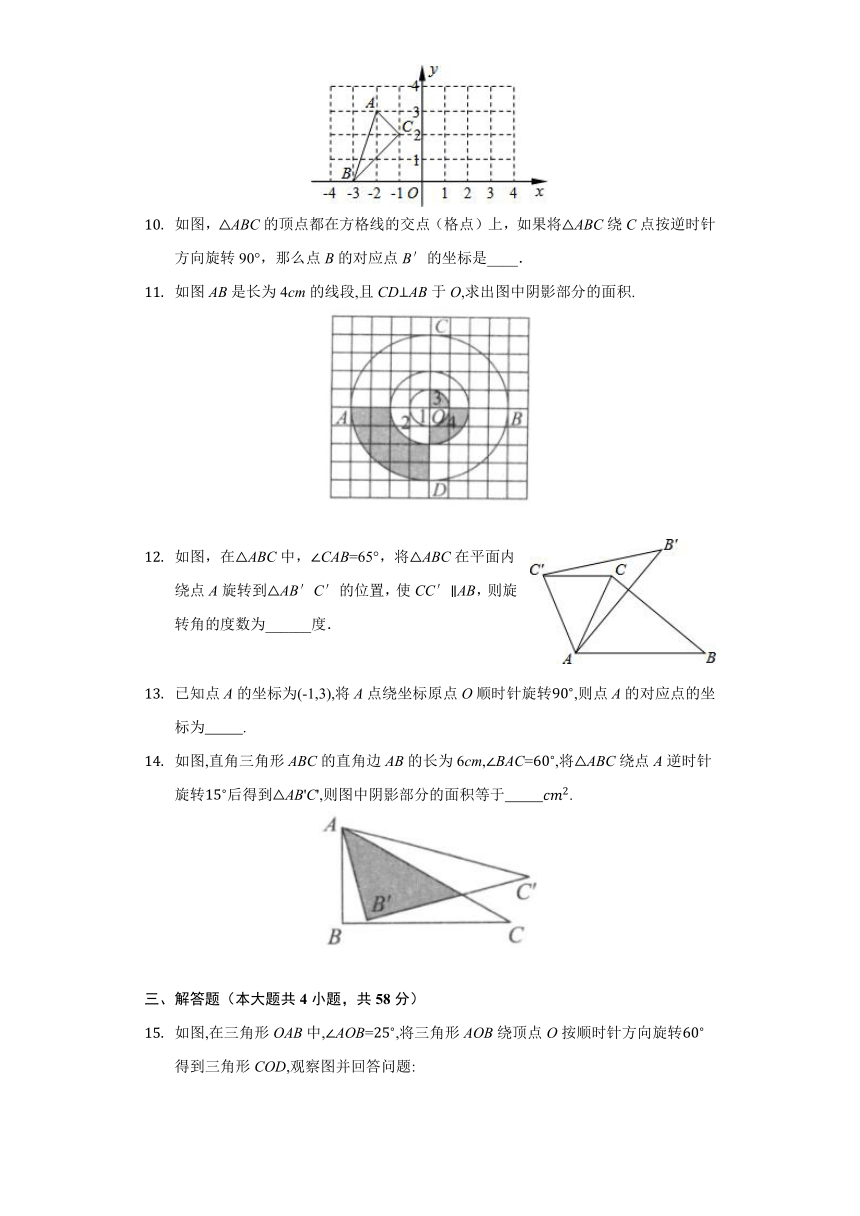
如图,两个全等的长方形ABCD与CDEF,旋转长方形ABCD能和长方形CDEF重合,则可以作为旋转中心的点有( )
A. 个 B. 个
C. 个 D. 无数个
把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
A. B.
C. D.
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图,点B,C,D在同一条直线上,△ABC和△ECD都是等边三角形,△EBC可以看作是△ ______ 绕点______ 逆时针旋转______ 度得到.
如图,△ABC的顶点都在方格线的交点(格点)上,如果将△ABC绕C点按逆时针方向旋转90°,那么点B的对应点B′的坐标是____.
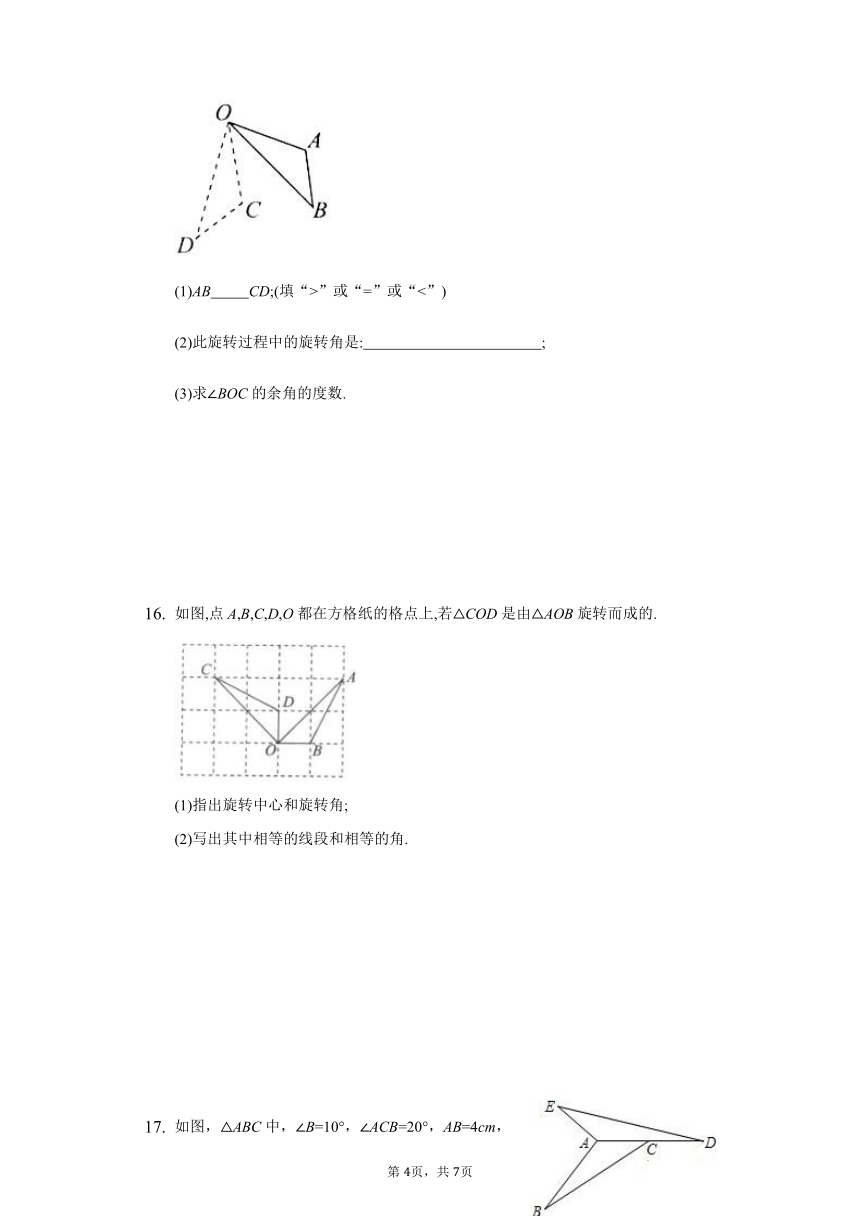
如图AB是长为4cm的线段,且CDAB于O,求出图中阴影部分的面积.
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为______度.
已知点A的坐标为(-1,3),将A点绕坐标原点O顺时针旋转,则点A的对应点的坐标为 .
如图,直角三角形ABC的直角边AB的长为6cm,BAC=,将ABC绕点A逆时针旋转后得到AB'C',则图中阴影部分的面积等于 .
三、解答题(本大题共4小题,共58分)
如图,在三角形OAB中,AOB=,将三角形AOB绕顶点O按顺时针方向旋转得到三角形COD,观察图并回答问题:
(1)AB CD;(填“>”或“=”或“<”)
(2)此旋转过程中的旋转角是: ;
(3)求BOC的余角的度数.
如图,点A,B,C,D,O都在方格纸的格点上,若COD是由AOB旋转而成的.
(1)指出旋转中心和旋转角;
(2)写出其中相等的线段和相等的角.
如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,三角形ABC按逆时针方向旋转一定角度后与三角形ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
如图,将一个钝角三角形ABC(其中ABC=)点B顺时针旋转得到,使得点C落在AB的延长线上的点处,连接.
(1)写出旋转角的度数;
(2)求证:=C.
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】DAC;C;60
10.【答案】(1,0)
11.【答案】 解;由题意可知阴影部分的面积为=().
12.【答案】50
13.【答案】(3,1)
14.【答案】18
15.【答案】解:(1)=;
(2)∠AOC和∠BOD;
(3)∵∠BOD=60°,∠DOC=∠BOA=25°,
∴∠BOC=∠BOD-∠COD=35°,
∴∠BOC的余角=90°-35°=55°.
16.【答案】(1)旋转中心是点O,旋转角是COA或DOB.
(2)相等的线段:AB=CD,AO=CO,BO=DO.
相等的角:COA=DOB,OCD=OAB,CDO=ABO,COD=AOB.
17.【答案】解:(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,
∴旋转中心是点A;
根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=150°,
∴旋转角度是150°;
(2)由(1)可知:∠BAE=360°-150°×2=60°,
由旋转可知:△ABC≌△ADE,
∴AB=AD,AC=AE,又C为AD中点,
∴AC=AE=AB=×4=2cm.
18.【答案】(1)解:∵∠ABC=120°,
∴∠CBC1=180°-∠ABC=180°-120°=60°,
∴旋转角为60°;
(2)证明:由题意可知:△ABC≌△A1BC1,
∴A1B=AB,∠C=∠C1,
由(1)知,∠ABA1=60°,
∴△A1AB是等边三角形,
∴∠BAA1=60°,
∴∠BAA1=∠CBC1,
∴AA1∥BC(同位角相等,两直线平行),
∴∠A1AC=∠C(两直线平行,内错角相等).
第6页,共7页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共24分)
如图,将△ABC绕点P顺时针旋转90°得到△A’B’C’,则点P的坐标是(▲)
A. B.
C. D.
如图,在下面的四个三角形中,不能由ABC经过旋转或平移得到的是( )
A. B.
C. D.
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
如图,△ABD 经过旋转后到达△ ACE 的位置,下列说法不正确的是().
A. 点是旋转中心 B. 是一个旋转角
C. D. ≌
同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图看到的是万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的平行四边形AEFG可以看成是把平行四边形ABCD以A为中心( )
A. 顺时针旋转得到 B. 顺时针旋转得到
C. 逆时针旋转得到 D. 逆时针旋转得到
如图,两个全等的长方形ABCD与CDEF,旋转长方形ABCD能和长方形CDEF重合,则可以作为旋转中心的点有( )
A. 个 B. 个
C. 个 D. 无数个
把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
A. B.
C. D.
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
A. B.
C. D.
二、填空题(本大题共6小题,共18分)
如图,点B,C,D在同一条直线上,△ABC和△ECD都是等边三角形,△EBC可以看作是△ ______ 绕点______ 逆时针旋转______ 度得到.
如图,△ABC的顶点都在方格线的交点(格点)上,如果将△ABC绕C点按逆时针方向旋转90°,那么点B的对应点B′的坐标是____.
如图AB是长为4cm的线段,且CDAB于O,求出图中阴影部分的面积.
如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为______度.
已知点A的坐标为(-1,3),将A点绕坐标原点O顺时针旋转,则点A的对应点的坐标为 .
如图,直角三角形ABC的直角边AB的长为6cm,BAC=,将ABC绕点A逆时针旋转后得到AB'C',则图中阴影部分的面积等于 .
三、解答题(本大题共4小题,共58分)
如图,在三角形OAB中,AOB=,将三角形AOB绕顶点O按顺时针方向旋转得到三角形COD,观察图并回答问题:
(1)AB CD;(填“>”或“=”或“<”)
(2)此旋转过程中的旋转角是: ;
(3)求BOC的余角的度数.
如图,点A,B,C,D,O都在方格纸的格点上,若COD是由AOB旋转而成的.
(1)指出旋转中心和旋转角;
(2)写出其中相等的线段和相等的角.
如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,三角形ABC按逆时针方向旋转一定角度后与三角形ADE重合,且点C恰好成为AD的中点.
(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
如图,将一个钝角三角形ABC(其中ABC=)点B顺时针旋转得到,使得点C落在AB的延长线上的点处,连接.
(1)写出旋转角的度数;
(2)求证:=C.
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】DAC;C;60
10.【答案】(1,0)
11.【答案】 解;由题意可知阴影部分的面积为=().
12.【答案】50
13.【答案】(3,1)
14.【答案】18
15.【答案】解:(1)=;
(2)∠AOC和∠BOD;
(3)∵∠BOD=60°,∠DOC=∠BOA=25°,
∴∠BOC=∠BOD-∠COD=35°,
∴∠BOC的余角=90°-35°=55°.
16.【答案】(1)旋转中心是点O,旋转角是COA或DOB.
(2)相等的线段:AB=CD,AO=CO,BO=DO.
相等的角:COA=DOB,OCD=OAB,CDO=ABO,COD=AOB.
17.【答案】解:(1)∵△ABC逆时针旋转一定角度后与△ADE重合,A为顶点,
∴旋转中心是点A;
根据旋转的性质可知:∠CAE=∠BAD=180°-∠B-∠ACB=150°,
∴旋转角度是150°;
(2)由(1)可知:∠BAE=360°-150°×2=60°,
由旋转可知:△ABC≌△ADE,
∴AB=AD,AC=AE,又C为AD中点,
∴AC=AE=AB=×4=2cm.
18.【答案】(1)解:∵∠ABC=120°,
∴∠CBC1=180°-∠ABC=180°-120°=60°,
∴旋转角为60°;
(2)证明:由题意可知:△ABC≌△A1BC1,
∴A1B=AB,∠C=∠C1,
由(1)知,∠ABA1=60°,
∴△A1AB是等边三角形,
∴∠BAA1=60°,
∴∠BAA1=∠CBC1,
∴AA1∥BC(同位角相等,两直线平行),
∴∠A1AC=∠C(两直线平行,内错角相等).
第6页,共7页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
