2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》优生辅导训练(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》优生辅导训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 306.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学上册《5.3三角形的中位线》优生辅导训练(附答案)
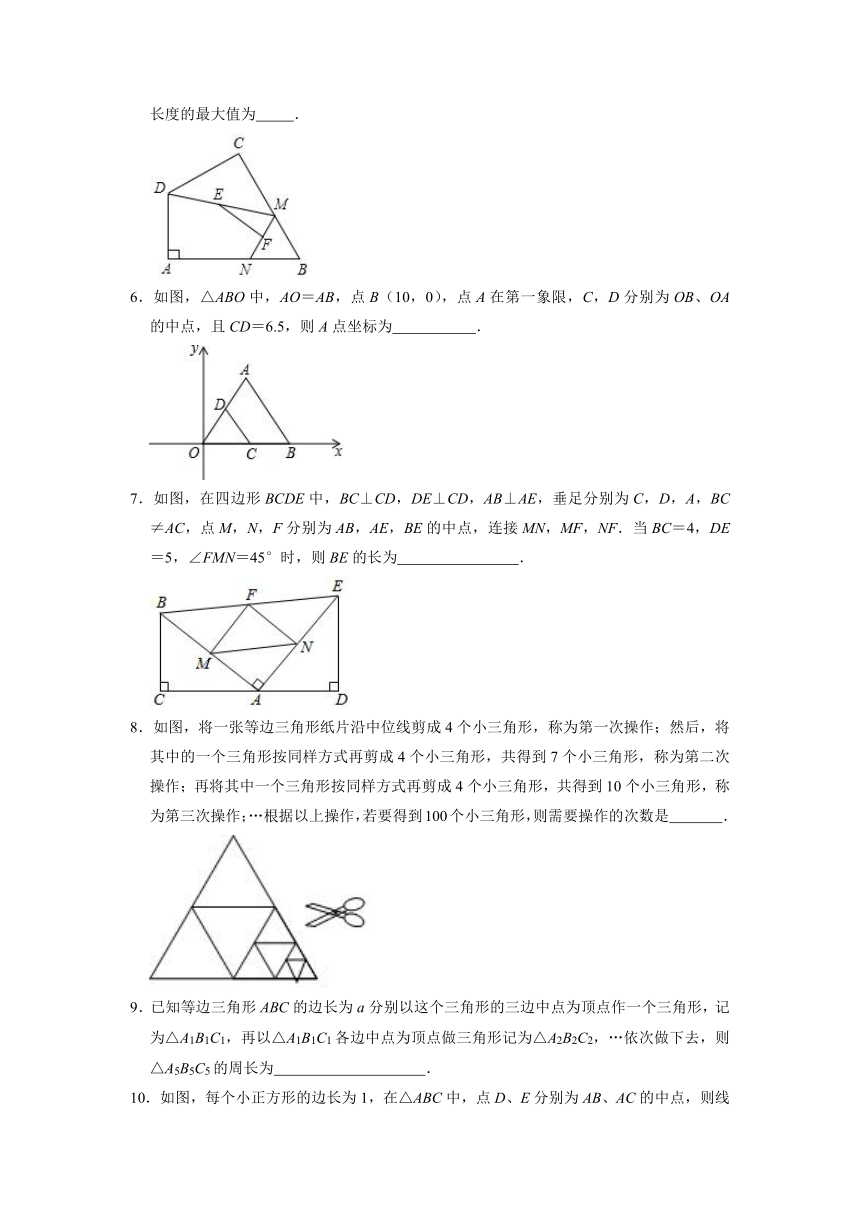
1.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
2.如图,在△ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.A,B两地被池塘隔开,小明先在AB外选一点C,然后分别步测出AC,BC的中点D,E,并测出DE的长为20m,则AB的长为( )
A.10m B.20m C.30m D.40m
4.如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长( )
A.只与AB、CD的长有关 B.只与AD、BC的长有关
C.只与AC、BD的长有关 D.与四边形ABCD各边的长都有关.
5.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
6.如图,△ABO中,AO=AB,点B(10,0),点A在第一象限,C,D分别为OB、OA的中点,且CD=6.5,则A点坐标为 .
7.如图,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,则BE的长为 .
8.如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是 .
9.已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A1B1C1,再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2,…依次做下去,则△A5B5C5的周长为 .
10.如图,每个小正方形的边长为1,在△ABC中,点D、E分别为AB、AC的中点,则线段DE的长为 .
11.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为 .
12.如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是 .
13.“数缺形时少直观,形少数时难入微”.小明学习上爱动脑,在计算的值时构造了这样一个图形:如图,正△ABC面积为,分别取AC、BC两边的中点D、E,再分别取CD、CE的中点,依次取下去…,能直观地求出它的值.也请你根据这个图形计算:= .
14.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,DE=2,求FC的长度.
15.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,连接MN,如果AB=10,BC=15,MN=3,求△ABC的周长.
16.如图,已知四边形ABCD的对角线AC与BD相交于点O,且AC=BD,M、N分别是AB、CD的中点,MN分别交BD、AC于点E、F.你能说出OE与OF的大小关系并加以证明吗?
17.在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在△ABC中,D、E分别是边AB、AC的中点.
求证:
证明:如图,延长DE到点F,使EF=DE,连接CF,
……
(1)补全求证;
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若CE=3,DF=8,求边AB的取值范围.
18.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
19.已知:如图,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为AB的中点,N为DC的中点.求证:∠PMN=∠PNM.
20.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
参考答案
1.解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
故选:C.
2.解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∵BC=16,
∴DE=BC=8.
∵∠AFB=90°,D是AB的中点,AB=10,
∴DF=AB=5,
∴EF=DE﹣DF=8﹣5=3.
故选:B.
3.解:∵点D,E是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=40m,
故选:D.
4.解:∵点E、F、G、H分别是线段AB、CD、AC、BD的中点,
∴四边形EGFH的周长=FG+GE+EH+FH=,
故选:B.
5.解:连接DN、DB,如图所示:
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD===4,
∵点E,F分别为DM,MN的中点,
∴EF是△DMN的中位线,
∴EF=DN,
由题意得,当点N与点B重合时DN最大,最大值为4,
∴EF长度的最大值为2,
故答案为:2.
6.解:如图,连接AC,
∵AO=AB,点C是OB的中点,
∴AC⊥BC,OC=OB=×10=5,
∵点D是AO的中点,
∴AO=2CD=2×6.5=13,
由勾股定理得,AC===12,
所以,点A(5,12).
故答案为:(5,12).
7.解:∵点M,N,F分别为AB,AE,BE的中点,
∴MF,MN都是△ABE的中位线,
∴MF∥AE,MN∥BE,
∴四边形EFMN是平行四边形,
∴∠AEB=∠NMF=45°,
又∵AB⊥AE,
∴∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AB=AE,
∵BC⊥CD,DE⊥CD,
又∵∠ABC+∠BAC=90°,∠EAD+∠BAC=90°,
∴∠ABC=∠EAD,
∵∠C=∠D=90°,
∴△ABC≌△EAD(AAS),
∴BC=AD=4,CA=DE=5,
∴Rt△ABC中,AB==,
∴等腰Rt△ABE中,BE==,
故答案为:.
8.解:∵第一次操作后,三角形共有4个;
第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n﹣1)=3n+1个;
当3n+1=100时,解得:n=33,
故答案为:33.
9.解:等边△ABC的边长为a,
∴等边△ABC的周长为3a.
∵A2、B2分别是边A1B1、B1C1的中点,
∴A2B2是△A1B1C1的中位线,
∴A2B2=A1B1.
同理,A2C2=A1C1,C2B2=C1B1.
∴△A2B2C2的周长=等边△A1B1C1的周长=.
同理,△A3B3C3的周长=△A2B2C2的周长=等边△A1B1C1的周长.
…,
∴△AnBn n的周长=△A1B1C1的周长=.
∴△A5B5C5的周长===.
故答案为:.
10.解:由勾股定理可知:BC==.
∵点D、E分别为AB、AC的中点,
∴DE=BC=.
故答案为:.
11.解:∵△ABC的周长是26,BC=10,
∴AB+AC=26﹣10=16,
∵∠ABC的平分线垂直于AE,
∴在△ABQ和△EBQ中,
,
∴△ABQ≌△EBQ,
∴AQ=EQ,AB=BE,
同理,AP=DP,AC=CD,
∴DE=BE+CD﹣BC=AB+AC﹣BC=16﹣10=6,
∵AQ=DP,AP=DP,
∴PQ是△ADE的中位线,
∴PQ=DE=3.
故答案是:3.
12.解:如图,延长AD、AE分别角BC与BC的延长线于M、N,
∵BD平分∠ABC,AD⊥BD于D,
∴AD=MD,AB=MB=7,
∵CE平分∠ACB的外角,AE⊥CE于E,
∴AE=EN,AC=CN=6,
∴DE是△AMN的中位线,
∵BC=9,
∴MN=CN+BC﹣BM=6+9﹣7=8,
∴DE=MN=×8=4.
故答案为:4.
13.解:设第n个小三角形的面积为sn,则sn=
根据中位线定理,得出小三角形的面积是对应梯形面积的
即sn= =
那么,s1+s2+s3+…+sn=(1﹣4﹣1+4﹣1﹣4﹣2+…+4﹣n﹣2﹣4﹣n﹣1+4﹣n﹣1﹣4﹣n)=
同时,s1+s2+s3+…+sn=
以上两式联立解得:=
14.解:∵AF⊥BC,点D是边AB的中点,DF=3,
∴AB=2DF=6.
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,
∴∠B=∠ADE=30°,
∴AF=AB=3,
由勾股定理得,BF===3,
∴FC=BC﹣BF=.
15.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=10,BN=ND,
∵BM=MC,
∴DC=2MN=6,
∴AC=AD+DC=16,
∴△ABC的周长=AB+BC+AC=10+15+16=41,
即△ABC的周长是41.
16.解:相等.理由如下:
取AD的中点G,连接MG,NG,
∵G、N分别为AD、CD的中点,
∴GN是△ACD的中位线,
∴GN=AC,
同理可得,GM=BD,
∵AC=BD,
∴GN=GM=AC=BD.
∴∠GMN=∠GNM,
又∵MG∥OE,NG∥OF,
∴∠OEF=∠GMN=∠GNM=∠OFE,
∴OE=OF.
17.解:(1)DE∥BC,且;
(2)∵点E是AC的中点,
∴AE=CE,
又∵EF=ED,∠AED=∠CEF,
∴△ADE≌△CFE(SAS),
∴AD=CF,∠A=∠ECF,
∴AD∥CF,
∴AB∥CF,
∵点D是AB的中点,
∴AD=BD,
∴BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC,
∵DE=FE,
∴;
(3)∵DF=8,
∴BC=8,
∵CE=3,
∴AC=6,
∴BC﹣AC<AB<BC+AC,
即2<AB<14.
18.解:(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=FC,
∵DE∥FC,
∴四边形DCFE是平行四边形,
∴CD=EF;
(2)猜想:△ABC的面积=四边形BDEF的面积,理由如下:
∵DE为△ABC的中位线,
∴DE∥BC,DE=BC
∴△ADE的面积=△DEC的面积,
∴四边形DCFE是平行四边形,
∴△DEC的面积=△ECF的面积,
∴△ADE的面积=△ECF的面积,
∴△ABC的面积=四边形BDEF的面积.
19.解:∵在四边形ABCD中,P是对角线BD的中点,M,N分别是AB,CD的中点,
∴NP,PM分别是△CDB与△DAB的中位线,
∴PN=BC,PM=AD,PN∥BC,PM∥AD,
∴∠NPD=∠DBC,∠MPB=∠ADB,
∵AD=BC,
∴PN=PM,
故△NMP是等腰三角形.
∴∠PMN=∠PNM.
20.证明:如图,连接BD,作BD的中点M,连接EM、FM.
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P
同理可证:FM∥CD,FM=CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
1.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
2.如图,在△ABC中,AB=10,BC=16,点D、E分别是边AB、AC的中点,点F是线段DE上的一点,连接AF、BF,若∠AFB=90°,则线段EF的长为( )
A.2 B.3 C.4 D.5
3.A,B两地被池塘隔开,小明先在AB外选一点C,然后分别步测出AC,BC的中点D,E,并测出DE的长为20m,则AB的长为( )
A.10m B.20m C.30m D.40m
4.如图,四边形ABCD中,点E、F、G、H分别是线段AB、CD、AC、BD的中点,则四边形EGFH的周长( )
A.只与AB、CD的长有关 B.只与AD、BC的长有关
C.只与AC、BD的长有关 D.与四边形ABCD各边的长都有关.
5.如图,四边形ABCD中,∠A=90°,AB=2,AD=2,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
6.如图,△ABO中,AO=AB,点B(10,0),点A在第一象限,C,D分别为OB、OA的中点,且CD=6.5,则A点坐标为 .
7.如图,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF.当BC=4,DE=5,∠FMN=45°时,则BE的长为 .
8.如图,将一张等边三角形纸片沿中位线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作;…根据以上操作,若要得到100个小三角形,则需要操作的次数是 .
9.已知等边三角形ABC的边长为a分别以这个三角形的三边中点为顶点作一个三角形,记为△A1B1C1,再以△A1B1C1各边中点为顶点做三角形记为△A2B2C2,…依次做下去,则△A5B5C5的周长为 .
10.如图,每个小正方形的边长为1,在△ABC中,点D、E分别为AB、AC的中点,则线段DE的长为 .
11.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为 .
12.如图,BD平分∠ABC,AD⊥BD于D,CE平分∠ACB的外角,AE⊥CE于E,AC=6,BC=9,AB=7,则DE的长是 .
13.“数缺形时少直观,形少数时难入微”.小明学习上爱动脑,在计算的值时构造了这样一个图形:如图,正△ABC面积为,分别取AC、BC两边的中点D、E,再分别取CD、CE的中点,依次取下去…,能直观地求出它的值.也请你根据这个图形计算:= .
14.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,DE=2,求FC的长度.
15.如图已知,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,连接MN,如果AB=10,BC=15,MN=3,求△ABC的周长.
16.如图,已知四边形ABCD的对角线AC与BD相交于点O,且AC=BD,M、N分别是AB、CD的中点,MN分别交BD、AC于点E、F.你能说出OE与OF的大小关系并加以证明吗?
17.在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在△ABC中,D、E分别是边AB、AC的中点.
求证:
证明:如图,延长DE到点F,使EF=DE,连接CF,
……
(1)补全求证;
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若CE=3,DF=8,求边AB的取值范围.
18.如图,在等边△ABC中,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:CD=EF;
(2)猜想:△ABC的面积与四边形BDEF的面积的关系,并说明理由.
19.已知:如图,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为AB的中点,N为DC的中点.求证:∠PMN=∠PNM.
20.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
参考答案
1.解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
故选:C.
2.解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∵BC=16,
∴DE=BC=8.
∵∠AFB=90°,D是AB的中点,AB=10,
∴DF=AB=5,
∴EF=DE﹣DF=8﹣5=3.
故选:B.
3.解:∵点D,E是AC,BC的中点,
∴DE是△ABC的中位线,
∴AB=2DE=40m,
故选:D.
4.解:∵点E、F、G、H分别是线段AB、CD、AC、BD的中点,
∴四边形EGFH的周长=FG+GE+EH+FH=,
故选:B.
5.解:连接DN、DB,如图所示:
在Rt△DAB中,∠A=90°,AB=2,AD=2,
∴BD===4,
∵点E,F分别为DM,MN的中点,
∴EF是△DMN的中位线,
∴EF=DN,
由题意得,当点N与点B重合时DN最大,最大值为4,
∴EF长度的最大值为2,
故答案为:2.
6.解:如图,连接AC,
∵AO=AB,点C是OB的中点,
∴AC⊥BC,OC=OB=×10=5,
∵点D是AO的中点,
∴AO=2CD=2×6.5=13,
由勾股定理得,AC===12,
所以,点A(5,12).
故答案为:(5,12).
7.解:∵点M,N,F分别为AB,AE,BE的中点,
∴MF,MN都是△ABE的中位线,
∴MF∥AE,MN∥BE,
∴四边形EFMN是平行四边形,
∴∠AEB=∠NMF=45°,
又∵AB⊥AE,
∴∠ABE=45°,
∴△ABE是等腰直角三角形,
∴AB=AE,
∵BC⊥CD,DE⊥CD,
又∵∠ABC+∠BAC=90°,∠EAD+∠BAC=90°,
∴∠ABC=∠EAD,
∵∠C=∠D=90°,
∴△ABC≌△EAD(AAS),
∴BC=AD=4,CA=DE=5,
∴Rt△ABC中,AB==,
∴等腰Rt△ABE中,BE==,
故答案为:.
8.解:∵第一次操作后,三角形共有4个;
第二次操作后,三角形共有4+3=7个;
第三次操作后,三角形共有4+3+3=10个;
…
∴第n次操作后,三角形共有4+3(n﹣1)=3n+1个;
当3n+1=100时,解得:n=33,
故答案为:33.
9.解:等边△ABC的边长为a,
∴等边△ABC的周长为3a.
∵A2、B2分别是边A1B1、B1C1的中点,
∴A2B2是△A1B1C1的中位线,
∴A2B2=A1B1.
同理,A2C2=A1C1,C2B2=C1B1.
∴△A2B2C2的周长=等边△A1B1C1的周长=.
同理,△A3B3C3的周长=△A2B2C2的周长=等边△A1B1C1的周长.
…,
∴△AnBn n的周长=△A1B1C1的周长=.
∴△A5B5C5的周长===.
故答案为:.
10.解:由勾股定理可知:BC==.
∵点D、E分别为AB、AC的中点,
∴DE=BC=.
故答案为:.
11.解:∵△ABC的周长是26,BC=10,
∴AB+AC=26﹣10=16,
∵∠ABC的平分线垂直于AE,
∴在△ABQ和△EBQ中,
,
∴△ABQ≌△EBQ,
∴AQ=EQ,AB=BE,
同理,AP=DP,AC=CD,
∴DE=BE+CD﹣BC=AB+AC﹣BC=16﹣10=6,
∵AQ=DP,AP=DP,
∴PQ是△ADE的中位线,
∴PQ=DE=3.
故答案是:3.
12.解:如图,延长AD、AE分别角BC与BC的延长线于M、N,
∵BD平分∠ABC,AD⊥BD于D,
∴AD=MD,AB=MB=7,
∵CE平分∠ACB的外角,AE⊥CE于E,
∴AE=EN,AC=CN=6,
∴DE是△AMN的中位线,
∵BC=9,
∴MN=CN+BC﹣BM=6+9﹣7=8,
∴DE=MN=×8=4.
故答案为:4.
13.解:设第n个小三角形的面积为sn,则sn=
根据中位线定理,得出小三角形的面积是对应梯形面积的
即sn= =
那么,s1+s2+s3+…+sn=(1﹣4﹣1+4﹣1﹣4﹣2+…+4﹣n﹣2﹣4﹣n﹣1+4﹣n﹣1﹣4﹣n)=
同时,s1+s2+s3+…+sn=
以上两式联立解得:=
14.解:∵AF⊥BC,点D是边AB的中点,DF=3,
∴AB=2DF=6.
∵点D,E分别是边AB,AC的中点,
∴DE∥BC,
∴∠B=∠ADE=30°,
∴AF=AB=3,
由勾股定理得,BF===3,
∴FC=BC﹣BF=.
15.解:延长BN交AC于D,
在△ANB和△AND中,
,
∴△ANB≌△AND(ASA),
∴AD=AB=10,BN=ND,
∵BM=MC,
∴DC=2MN=6,
∴AC=AD+DC=16,
∴△ABC的周长=AB+BC+AC=10+15+16=41,
即△ABC的周长是41.
16.解:相等.理由如下:
取AD的中点G,连接MG,NG,
∵G、N分别为AD、CD的中点,
∴GN是△ACD的中位线,
∴GN=AC,
同理可得,GM=BD,
∵AC=BD,
∴GN=GM=AC=BD.
∴∠GMN=∠GNM,
又∵MG∥OE,NG∥OF,
∴∠OEF=∠GMN=∠GNM=∠OFE,
∴OE=OF.
17.解:(1)DE∥BC,且;
(2)∵点E是AC的中点,
∴AE=CE,
又∵EF=ED,∠AED=∠CEF,
∴△ADE≌△CFE(SAS),
∴AD=CF,∠A=∠ECF,
∴AD∥CF,
∴AB∥CF,
∵点D是AB的中点,
∴AD=BD,
∴BD=CF,
∴四边形BDFC是平行四边形,
∴DE∥BC,DF=BC,
∵DE=FE,
∴;
(3)∵DF=8,
∴BC=8,
∵CE=3,
∴AC=6,
∴BC﹣AC<AB<BC+AC,
即2<AB<14.
18.解:(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=BC,
∵CF=BC,
∴DE=FC,
∵DE∥FC,
∴四边形DCFE是平行四边形,
∴CD=EF;
(2)猜想:△ABC的面积=四边形BDEF的面积,理由如下:
∵DE为△ABC的中位线,
∴DE∥BC,DE=BC
∴△ADE的面积=△DEC的面积,
∴四边形DCFE是平行四边形,
∴△DEC的面积=△ECF的面积,
∴△ADE的面积=△ECF的面积,
∴△ABC的面积=四边形BDEF的面积.
19.解:∵在四边形ABCD中,P是对角线BD的中点,M,N分别是AB,CD的中点,
∴NP,PM分别是△CDB与△DAB的中位线,
∴PN=BC,PM=AD,PN∥BC,PM∥AD,
∴∠NPD=∠DBC,∠MPB=∠ADB,
∵AD=BC,
∴PN=PM,
故△NMP是等腰三角形.
∴∠PMN=∠PNM.
20.证明:如图,连接BD,作BD的中点M,连接EM、FM.
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P
同理可证:FM∥CD,FM=CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
