2021-2022学年北师大版九年级数学下册第3章圆 单元综合达标测试题 (Word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章圆 单元综合达标测试题 (Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 652.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 22:27:30 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《第3章圆》单元综合达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
2.如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为( )
A.120° B.125° C.135° D.140°
3.如图,△ABC是⊙O的内接三角形,将劣弧沿AC折叠后刚好经过弦BC的中点D.若AC=6,∠C=60°,则⊙O的半径长为( )
A. B. C. D.
4.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
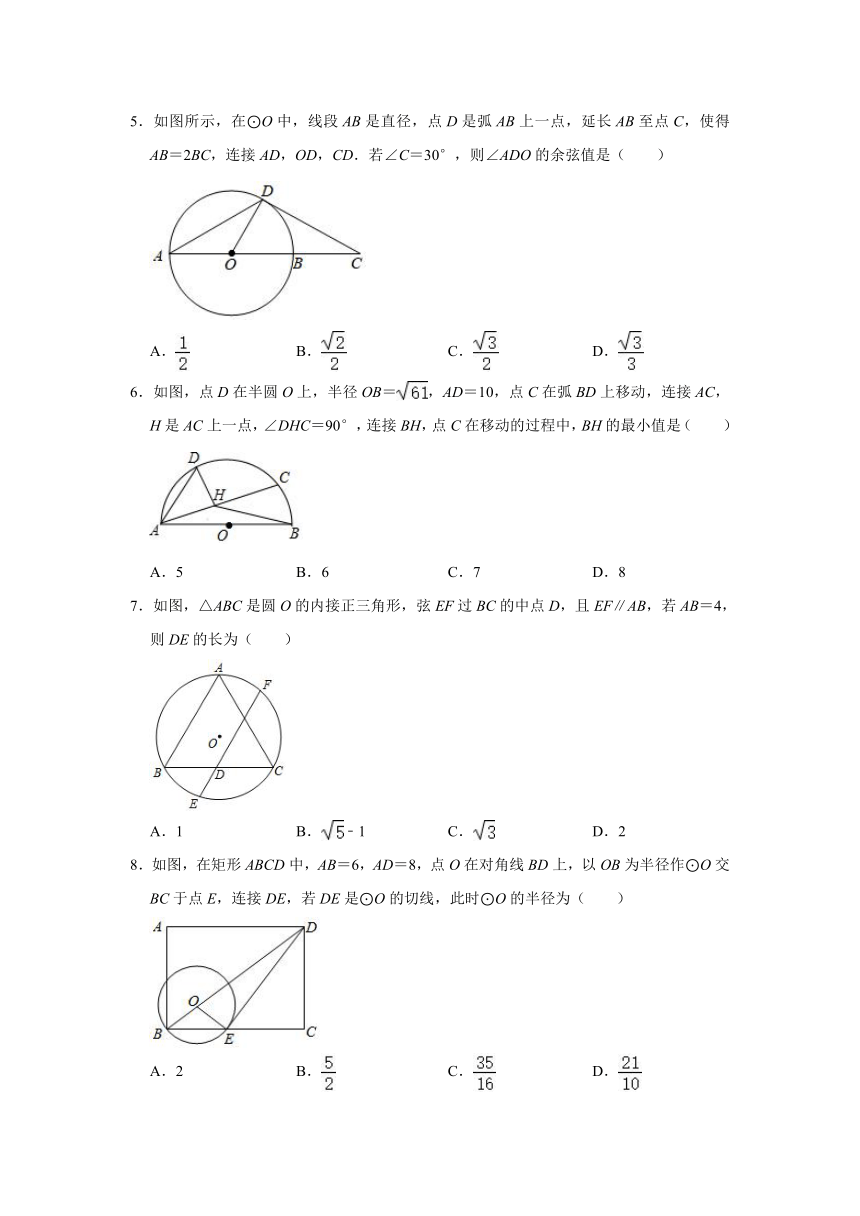
5.如图所示,在⊙O中,线段AB是直径,点D是弧AB上一点,延长AB至点C,使得AB=2BC,连接AD,OD,CD.若∠C=30°,则∠ADO的余弦值是( )
A. B. C. D.
6.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
7.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
8.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE,若DE是⊙O的切线,此时⊙O的半径为( )
A.2 B. C. D.
二.填空题(共8小题,满分40分)
9.如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
10.如图,平面直角坐标系xOy中,点A的坐标为(5,3),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
11.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆O上一动点,CF⊥AE于F,当点E在圆O的运动过程中,线段FG的长度的最小值为 .
12.已知直线l:y=﹣x+2,若⊙P的半径为1,圆心P在y轴上,当⊙P与直线l相切时,则点P的坐标是 .
13.如图,⊙O是锐角三角形ABC的外接圆,AB=8,∠ACB=60°,且BC>AC,点D是△ABC高线的交点,连接AD,BD,CD,则∠ADB的度数为 ,CD的长为 .
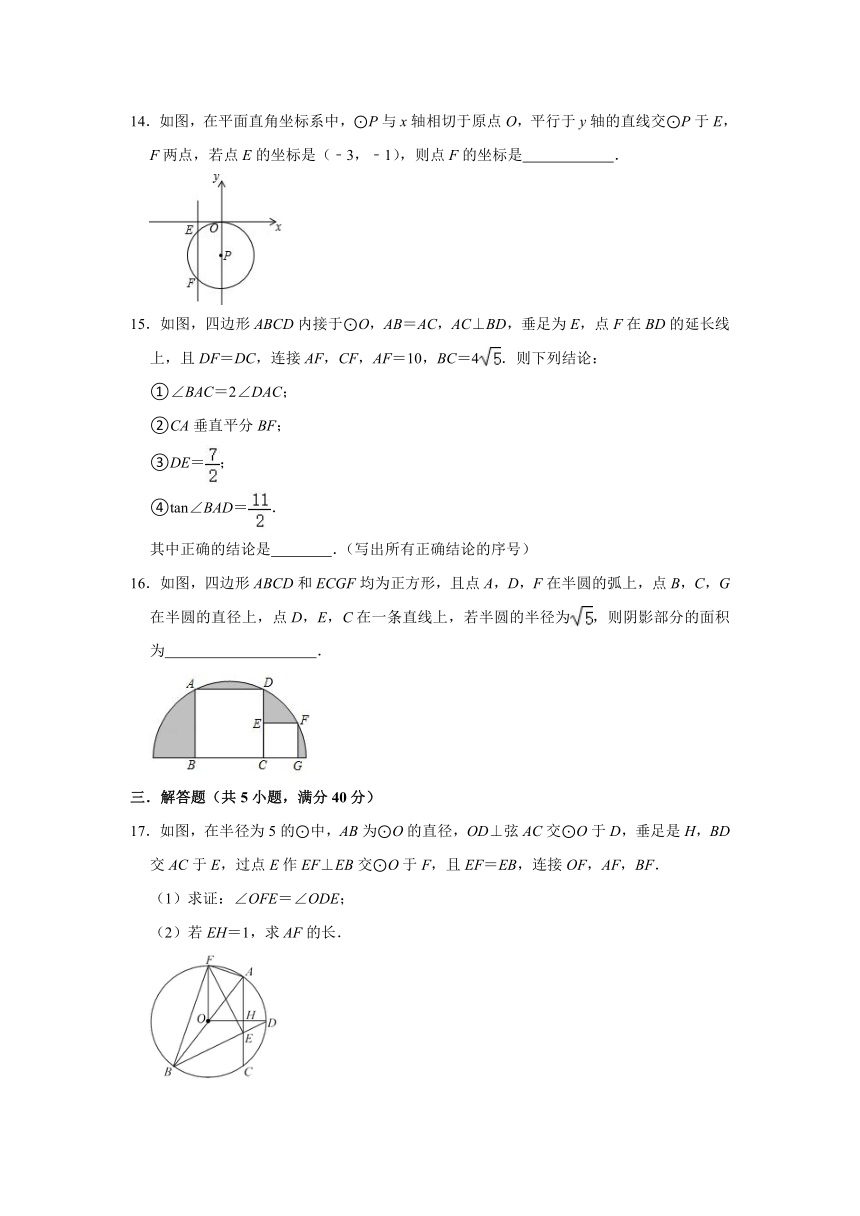
14.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(﹣3,﹣1),则点F的坐标是 .
15.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF,CF,AF=10,BC=4.则下列结论:
①∠BAC=2∠DAC;
②CA垂直平分BF;
③DE=;
④tan∠BAD=.
其中正确的结论是 .(写出所有正确结论的序号)
16.如图,四边形ABCD和ECGF均为正方形,且点A,D,F在半圆的弧上,点B,C,G在半圆的直径上,点D,E,C在一条直线上,若半圆的半径为,则阴影部分的面积为 .
三.解答题(共5小题,满分40分)
17.如图,在半径为5的⊙中,AB为⊙O的直径,OD⊥弦AC交⊙O于D,垂足是H,BD交AC于E,过点E作EF⊥EB交⊙O于F,且EF=EB,连接OF,AF,BF.
(1)求证:∠OFE=∠ODE;
(2)若EH=1,求AF的长.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
19.如图,△ABC内接于⊙O,BA=BC,直径AD交BC于E,延长CD交切线BF于F.
(1)求证:∠BFC=90°
(2)若tan∠BAD=,CD=2,求CE的长.
20.如图,O为平行四边形ABCD的边AD上一点,AO=AB,以OD为半径的⊙O交AD于点E,交CD于点F,OG⊥EF交BC于点G,⊙O和AG相切于点P.
(1)求证:四边形ABGO为菱形;
(2)若AB=6,cos∠ADC=,求⊙O的半径R.
21.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,过点C作CH⊥BO的延长线于点H,
∵点O为△ABC的内心,∠A=60°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=90°+A=120°,
∴∠COH=60°,
∵OB=2,OC=4,
∴OH=2
∴CH=2,
∴△OBC的面积=OB CH=2×2=2.
故选:B.
2.解:∵点O是△ABC的外心,
∴∠AOB=2∠C,
∴∠C=∠AOB,
∵点I是△ABC的内心,
∴∠IAB=∠CAB,∠IBA=∠CBA,
∴∠AIB=180°﹣(∠IAB+∠IBA)
=180°﹣(∠CAB+∠CBA),
=180°﹣(180°﹣∠C)
=90°+∠C,
∴2∠AIB=180°+∠C,
∵∠AOB=2∠C,
∴∠AIB=90°+∠AOB,
∴4∠AIB﹣∠AOB=360°.
∵∠AIB=125°,
∴∠AOB=140°.
故选:D.
3.解:如图1,设折叠后的所在圆的圆心为O′,连接O′A,O′D,
∴∠AO′D=2∠ACB=120°,
连接OA,OB,
同理,∠AOB=120°,
∴∠AOB=∠AO′D,
∵⊙O与⊙O′是等圆,
∴AB=AD,
设⊙O的半径为R,
过O作OG⊥AB于G,
∵OA=OB,∠AOB=120°,
∴∠OAB=∠OBA=30°,AB=2AG,
∴OG=,
∴,
∴,
如图2,过A作AM⊥BC于M,
∵AB=AD,
∴可设BM=DM=x,则BD=2x,
∵D为BC的中点,
∴CD=BD=2x,
∴MC=DM+CD=3x,
∵AM⊥BC,∠ACB=60°,
∴∠MAC=30°,
在Rt△AMC中,MC=,
∴3x=3,
∴x=1,
∴AM=,BM=x=1,
在Rt△ABM中,AB=,
∵,
∴,
故选:D.
4.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
5.解:过点O作OD′⊥CD于D′.
∵∠OD′C=90°,∠C=30°,
∴OC=2OD′,
∵AB=2BC,OA=OB,
∴OC=2OA=2OD,
∴D与D′重合,
∴∠DOC=90°﹣30°=60°,
∵OA=OD,
∴∠OAD=∠ODA=30°,
∴cos∠ADO=,
故选:C.
6.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
7.解:如图.过C作CN⊥AB于N,交EF于M,
∵EF∥AB,
∴CM⊥EF.
根据圆和等边三角形的性质知:CN必过点O.
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
∴DG=AB=2;
∵△CGD是等边三角形,CM⊥DG,
∴DM=MG;
∵OM⊥EF,由垂径定理得:EM=MF,
∴DE=GF.
∵弦BC、EF相交于点D,
∴BD DC=DE DF,即DE×(DE+2)=4;
解得DE=﹣1(负值舍去).
故选:B.
8.解:如图,过点O作OF⊥BE于点F,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,BC=AD=8,DC=AB=6,
在Rt△ADB中,∠C=90°,
∴BD==10,
∴tan∠DBC===,
设OF=3x,BF=4x,
则BO=5x,
∵OB=OE,
∴BF=EF=4x,
∴CE=CB﹣BE=8﹣8x,
∵DE是⊙O的切线,
∴OE⊥DE,
∴∠OEF+∠DEC=90°,
∵∠DEC+∠EDC=90°,
∴∠OEF=∠EDC,
∵∠OFE=∠DCE,
∴△OEF∽△EDC,
∴=,
∴=,
解得x=0(舍去),x=,
∴OB=5x=.
故选:C.
二.填空题(共8小题,满分40分)
9.解:如图,连接OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=,
∴OA=,OF=BF=,
∴DF=BD﹣BF=,
∴OG=,GD=,
在Rt△AGO中,AG==,
∴AD=AG+GD=.
故答案为:.
10.解:过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
当点P在点D是上方时,如图,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形,
∴AC=OD,OC=AD,
∵⊙A与x轴相切,
∴AC为⊙A的半径,
∵点A坐标为(5,3),
∴AC=OD=3,OC=AD=5,
∵PB是切线,
∴AB⊥PB,
∵∠APB=30°,
∴PA=2AB=6,
在Rt△PAD中,根据勾股定理得,
PD===,
∴OP=PD+DO=3+,
∵点P在y轴的正半轴上,
∴点P坐标为(0,3+),
故答案为:(0,3+).
11.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
12.解:当x=0时,y=2;当y=0时,x=4.
∴A(0,2),B(4,0).
∴OA=2,OB=4,
∴AB==2,
当⊙P在y轴上从下向上运动时⊙P与直线AB有两种相切情况.
第一种情况:如图,当⊙P在直线l:y=﹣x+2与y轴交点下方与直线l相切时,过P1作P1D1⊥l于D1,
在Rt△D1P1A中,D1P1=1.
∵Rt△D1P1A∽Rt△OBA,
∴=,
∴=,
∴AP1=,
∴OP1=OA﹣AP1=2﹣,
∴P1坐标为(0,2﹣);
第二种情况:如图,当⊙P在直线l:y=﹣x+2与y轴交点上方与直线AB相切时,过P2作P2D2⊥l轴于D2,
同上可得OP2=OA+AP2=2+,
∴P2点的坐标为(0,2+).
∴P点的坐标为(0,2﹣)或(0,2+).
故答案为:(0,2﹣)或(0,2+).
13.解:连结AO,并延长交⊙O于E,连结EC,延长BD交AC于F,
∵AE为直径,
∴∠ACE=∠ABE=90°,
∵点D是△ABC高线的交点,
∴BF⊥AC,AG⊥BC,CD⊥AB,
∴∠CFB=∠CGA=90°,
∴∠FDG=360°﹣90°﹣90°﹣60°=120°,
∴∠ADB=∠FDG=120°,
∵∠ACE=∠CFB=90°,CD⊥AB,EB⊥AB,
∴CE∥DB,CD∥EB,
∴四边形CDBE为平行四边形,
∴CD=BE,
∵=,
∴∠ACB=∠AEB=60°,
∴∠EAB=90°﹣∠AEB=90°﹣60°=30°,
在Rt△ABE中,
BE=AB×tan30°=8×=,
∴CD=BE=.
故答案为:120°;.
14.解:过点P作AP⊥EF交EF于点A,连接PE,设OP=x,
∵⊙P与x轴相切于原点O,
∴OP⊥OB,
∵平行于y轴的直线交⊙P于E,F两点,
∴四边形APOB是矩形,
∴AB=OP=x,
∵点E的坐标是(﹣3,﹣1),
∴AP=OB=3,AE=AB﹣BE=x﹣1,
在Rt△ABE中,32+(x﹣1)2=x2,
解得x=5,
∴AE=4,
∵AF=AE,
∴EF=8,
∴BF=EF+BE=9,
∴点F的坐标是(﹣3,﹣9).
故答案为(﹣3,﹣9).
15.解:∵AB=AC,
∴=,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=(180°﹣∠BAC)=90°﹣∠BAC,
∵BD⊥AC,
∴∠ADB=90°﹣∠CAD,
∴∠BAC=∠CAD,
∴∠BAC=2∠CAD,故①正确,
∵DF=DC,
∴∠DFC=∠DCF,
∴∠BDC=2∠DFC,
∴∠BFC=∠BDC=∠BAC=∠FBC,
∴CB=CF,
又BD⊥AC,
∴AC是线段BF的中垂线,故②正确,
AB=AF=10,AC=10.
又BC=4,
设AE=x,CE=10﹣x,
由AB2﹣AE2=BC2﹣CE2,得100﹣x2=80﹣(10﹣x)2,
解得x=6,
∴AE=6,BE=8,CE=4,
∴DE===3,故③错误,
过点D作DH⊥AB于H.
∵∠DBH=∠ABE,∠BHD=∠AEB=90°,
∴△DBH∽△ABE,
∵==,
∴==,
∴BH=,DH=,
∴AH=AB﹣BH=10﹣=,
∴tan∠BAD===,故④正确.
故答案为:①②④.
16.解:连接OA,OF,设正方形ABCD的边长为a,正方形EFGD的边长为b,⊙O的半径为R.
则OB=,OG=,
而OC=BC﹣OB=OG﹣CG,
∴有:a﹣=﹣b得到:+=a+b,
两边平方得:R2﹣a2+2 +R2﹣b2=a2+2ab+b2
整理得: =a2+b2+ab﹣R2
两边再次平方得:R4﹣(a2+b2)R2+a2b2=(a2+b2+ab)2﹣2(a2+b2+ab)R2+R4,
整理得:a2+b2=R2=5,
∴阴影部分的面积=×π×5﹣5=π﹣5.
故答案为:π﹣5.
三.解答题(共5小题,满分40分)
17.(1)证明:连接OE.
在△OEF和△OEB中,
,
∴△OEF≌△OEB(SSS),
∴∠OFE=∠OBE,
∵OB=OD,
∴∠OBE=∠ODE,
∴∠OFE=∠ODE.
(2)∵AB是直径,
∴∠AFB=90°,
∵EF⊥BE,
∴∠BEF=90°,
∵EF=EB,
∴∠EFB=∠EFA=45°,
∵△OEF≌△OEB,
∴∠OEF=∠OEB=45°,
∴∠AFE=∠OEF=45°,
∴AF∥OE,
∵∠OFE=∠ODE,
∴∠FOH=∠DEF=90°,
∵OD⊥AC,
∴∠AOF=∠AHD=90°,
∴AO∥AE,
∴四边形AEOF是平行四边形,
∴OF=AE=5,AF=OE,
∵EH=1,
∴AH=AE﹣EH=4,
∴OH===3,
∴OE===,
∴AF=.
18.(1)证明:∵四边形ACDG是⊙O的内接四边形,
∴∠ACD+∠AGD=180°,
∵∠AGD+∠DGF=180°,
∴∠ACD=∠DGF,
∵CD⊥AB,AB为直径,
∴=,
∴∠AGC=∠ACD,
∴∠DGF=∠AGC.
(2)∵∠DGF=∠ACD,∠F=∠F,
∴△FDG∽△FAC,
∴=,
∴FD FC=FG FA,
∵CD⊥AB,
∴tanF==,
∵ED=DF,
∴EF=2DE,
∵==,
∴==,
∴∠ACD=60°,
∴∠CAE=30°,
∴AC=2CE,
设CE=DE=DF=x,则AE=x,AC=2x,FC=3x,
在Rt△AEF中,由勾股定理得AF==x,
∵FD FC=FA FG,
∴x 3x=6x,
解得x=0(舍)或x=2,
∴AC=2x=4.
19.(1)证明:延长BO交AC于H,连接OC,如图,
∵AD为直径,
∴∠ACD=90°,
∵BA=BC,OA=OC,
∴BH垂直平分AC,
∵BF为⊙O的切线,
∴BH⊥BF,
∴BF∥AC,
∴∠ACD+∠BFC=180°,
∴∠BFC=90°;
(2)解:∵BH⊥AC,∠ACD=90°,
∴BH∥CF,
∴∠BCD=∠HBC,
∵∠BCD=∠BAD,
∴∠HBC=∠BAD,
∴tan∠HBC=tan∠BAD=,
∵OA=OD,AH=CH,
∴OH=CD=1,
在Rt△BCH中,设⊙O的半径为r,
∵tan∠HBC==,
∴CH=(r+1),
在Rt△OCH中,12+(r+1)2=r2,解得r1=,r2=﹣1(舍去),
∴BO=,BH=,CH=,
在Rt△BCH中,BC===,
∵OB∥CD,
∴===,
∴=,
∴CE=CB=×=.
20.解:(1)∵DE为⊙O的直径,
∴∠EFD=90°,
∴DF⊥EF,
∵OG⊥EF,
∴OG∥CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵AB∥OG,
∴四边形ABGO为平行四边形,
∵AO=AB,
∴四边形ABGO为菱形;
(2)如图,连接OB,过点O作OH⊥BC于点H,
∵四边形ABGO为菱形,
∴OB⊥AG,
∵⊙O和AG相切于点P.
∴OP⊥AG,
∴O,P,B三点共线,OP=OB,
∵∠D=∠OGH,AB=6,
∴BG=OG=6,
∴GH=OG cos∠OGH=6×=2,
由勾股定理,得OH==4,
∴OB==4.
∴⊙O的半径R为2.
21.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵,,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PCB=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
(3)∵CM∥BP,
∴四边形PBCM为梯形,
作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP,AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+AMB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=,
∴S四边形PBCM=(PB+CM)×PH=(2+3)×=;
(4)过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,
∵∠APC=∠BPC=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴PQ=PB=1,
在Rt△BPQ中,BQ=,
在Rt△AQB中,AB=,
∵△ABC为等边三角形,
∴AN经过圆心O,
∴BN=AB=,
∴AN=,
在Rt△BON中,设BO=x,则ON=,
∴,
解得:x=,
∵∠BOA=∠BCA=120°,
∴的长度为.
一.选择题(共8小题,满分40分)
1.如图,点O为△ABC的内心,∠A=60°,OB=2,OC=4,则△OBC的面积是( )
A. B. C.2 D.4
2.如图,点I和O分别是△ABC的内心和外心,若∠AIB=125°,则∠AOB的度数为( )
A.120° B.125° C.135° D.140°
3.如图,△ABC是⊙O的内接三角形,将劣弧沿AC折叠后刚好经过弦BC的中点D.若AC=6,∠C=60°,则⊙O的半径长为( )
A. B. C. D.
4.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3 B.4 C.5 D.6
5.如图所示,在⊙O中,线段AB是直径,点D是弧AB上一点,延长AB至点C,使得AB=2BC,连接AD,OD,CD.若∠C=30°,则∠ADO的余弦值是( )
A. B. C. D.
6.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
7.如图,△ABC是圆O的内接正三角形,弦EF过BC的中点D,且EF∥AB,若AB=4,则DE的长为( )
A.1 B.﹣1 C. D.2
8.如图,在矩形ABCD中,AB=6,AD=8,点O在对角线BD上,以OB为半径作⊙O交BC于点E,连接DE,若DE是⊙O的切线,此时⊙O的半径为( )
A.2 B. C. D.
二.填空题(共8小题,满分40分)
9.如图,⊙O是△ABC的外接圆,∠BAC==45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则AD的长是 .
10.如图,平面直角坐标系xOy中,点A的坐标为(5,3),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
11.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为圆O上一动点,CF⊥AE于F,当点E在圆O的运动过程中,线段FG的长度的最小值为 .
12.已知直线l:y=﹣x+2,若⊙P的半径为1,圆心P在y轴上,当⊙P与直线l相切时,则点P的坐标是 .
13.如图,⊙O是锐角三角形ABC的外接圆,AB=8,∠ACB=60°,且BC>AC,点D是△ABC高线的交点,连接AD,BD,CD,则∠ADB的度数为 ,CD的长为 .
14.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(﹣3,﹣1),则点F的坐标是 .
15.如图,四边形ABCD内接于⊙O,AB=AC,AC⊥BD,垂足为E,点F在BD的延长线上,且DF=DC,连接AF,CF,AF=10,BC=4.则下列结论:
①∠BAC=2∠DAC;
②CA垂直平分BF;
③DE=;
④tan∠BAD=.
其中正确的结论是 .(写出所有正确结论的序号)
16.如图,四边形ABCD和ECGF均为正方形,且点A,D,F在半圆的弧上,点B,C,G在半圆的直径上,点D,E,C在一条直线上,若半圆的半径为,则阴影部分的面积为 .
三.解答题(共5小题,满分40分)
17.如图,在半径为5的⊙中,AB为⊙O的直径,OD⊥弦AC交⊙O于D,垂足是H,BD交AC于E,过点E作EF⊥EB交⊙O于F,且EF=EB,连接OF,AF,BF.
(1)求证:∠OFE=∠ODE;
(2)若EH=1,求AF的长.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,CD的延长线交于点F,连接CG,DG.
(1)求证:∠DGF=∠AGC.
(2)当ED=DF,GF=6,tanF=时,求AC的长.
19.如图,△ABC内接于⊙O,BA=BC,直径AD交BC于E,延长CD交切线BF于F.
(1)求证:∠BFC=90°
(2)若tan∠BAD=,CD=2,求CE的长.
20.如图,O为平行四边形ABCD的边AD上一点,AO=AB,以OD为半径的⊙O交AD于点E,交CD于点F,OG⊥EF交BC于点G,⊙O和AG相切于点P.
(1)求证:四边形ABGO为菱形;
(2)若AB=6,cos∠ADC=,求⊙O的半径R.
21.如图,等边△ABC内接于⊙O,P是上任一点(点P与点A、B重合),连接AP、BP,过点C作CM∥BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数;
(2)求证:△ACM≌△BCP;
(3)若PA=1,PB=2,求四边形PBCM的面积;
(4)在(3)的条件下,求的长度.
参考答案
一.选择题(共8小题,满分40分)
1.解:如图,过点C作CH⊥BO的延长线于点H,
∵点O为△ABC的内心,∠A=60°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=90°+A=120°,
∴∠COH=60°,
∵OB=2,OC=4,
∴OH=2
∴CH=2,
∴△OBC的面积=OB CH=2×2=2.
故选:B.
2.解:∵点O是△ABC的外心,
∴∠AOB=2∠C,
∴∠C=∠AOB,
∵点I是△ABC的内心,
∴∠IAB=∠CAB,∠IBA=∠CBA,
∴∠AIB=180°﹣(∠IAB+∠IBA)
=180°﹣(∠CAB+∠CBA),
=180°﹣(180°﹣∠C)
=90°+∠C,
∴2∠AIB=180°+∠C,
∵∠AOB=2∠C,
∴∠AIB=90°+∠AOB,
∴4∠AIB﹣∠AOB=360°.
∵∠AIB=125°,
∴∠AOB=140°.
故选:D.
3.解:如图1,设折叠后的所在圆的圆心为O′,连接O′A,O′D,
∴∠AO′D=2∠ACB=120°,
连接OA,OB,
同理,∠AOB=120°,
∴∠AOB=∠AO′D,
∵⊙O与⊙O′是等圆,
∴AB=AD,
设⊙O的半径为R,
过O作OG⊥AB于G,
∵OA=OB,∠AOB=120°,
∴∠OAB=∠OBA=30°,AB=2AG,
∴OG=,
∴,
∴,
如图2,过A作AM⊥BC于M,
∵AB=AD,
∴可设BM=DM=x,则BD=2x,
∵D为BC的中点,
∴CD=BD=2x,
∴MC=DM+CD=3x,
∵AM⊥BC,∠ACB=60°,
∴∠MAC=30°,
在Rt△AMC中,MC=,
∴3x=3,
∴x=1,
∴AM=,BM=x=1,
在Rt△ABM中,AB=,
∵,
∴,
故选:D.
4.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
5.解:过点O作OD′⊥CD于D′.
∵∠OD′C=90°,∠C=30°,
∴OC=2OD′,
∵AB=2BC,OA=OB,
∴OC=2OA=2OD,
∴D与D′重合,
∴∠DOC=90°﹣30°=60°,
∵OA=OD,
∴∠OAD=∠ODA=30°,
∴cos∠ADO=,
故选:C.
6.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
7.解:如图.过C作CN⊥AB于N,交EF于M,
∵EF∥AB,
∴CM⊥EF.
根据圆和等边三角形的性质知:CN必过点O.
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
∴DG=AB=2;
∵△CGD是等边三角形,CM⊥DG,
∴DM=MG;
∵OM⊥EF,由垂径定理得:EM=MF,
∴DE=GF.
∵弦BC、EF相交于点D,
∴BD DC=DE DF,即DE×(DE+2)=4;
解得DE=﹣1(负值舍去).
故选:B.
8.解:如图,过点O作OF⊥BE于点F,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,BC=AD=8,DC=AB=6,
在Rt△ADB中,∠C=90°,
∴BD==10,
∴tan∠DBC===,
设OF=3x,BF=4x,
则BO=5x,
∵OB=OE,
∴BF=EF=4x,
∴CE=CB﹣BE=8﹣8x,
∵DE是⊙O的切线,
∴OE⊥DE,
∴∠OEF+∠DEC=90°,
∵∠DEC+∠EDC=90°,
∴∠OEF=∠EDC,
∵∠OFE=∠DCE,
∴△OEF∽△EDC,
∴=,
∴=,
解得x=0(舍去),x=,
∴OB=5x=.
故选:C.
二.填空题(共8小题,满分40分)
9.解:如图,连接OA,过O点作OF⊥BC于F,作OG⊥AE于G,
∵⊙O是△ABC的外接圆,∠BAC=45°,
∴∠BOC=90°,
∵BD=4,CD=1,
∴BC=4+1=5,
∴OB=OC=,
∴OA=,OF=BF=,
∴DF=BD﹣BF=,
∴OG=,GD=,
在Rt△AGO中,AG==,
∴AD=AG+GD=.
故答案为:.
10.解:过点A分别作AC⊥x轴于点C、AD⊥y轴于点D,连接AB,
当点P在点D是上方时,如图,
∵AD⊥y轴,AC⊥x轴,
∴四边形ADOC为矩形,
∴AC=OD,OC=AD,
∵⊙A与x轴相切,
∴AC为⊙A的半径,
∵点A坐标为(5,3),
∴AC=OD=3,OC=AD=5,
∵PB是切线,
∴AB⊥PB,
∵∠APB=30°,
∴PA=2AB=6,
在Rt△PAD中,根据勾股定理得,
PD===,
∴OP=PD+DO=3+,
∵点P在y轴的正半轴上,
∴点P坐标为(0,3+),
故答案为:(0,3+).
11.解:作GM⊥AC于M,连接AG.
∵GO⊥AB,
∴OA=OB,
在Rt△AGO中,AG=2,OG=1,
∴AG=2OG,OA===,
∴∠GAO=30°,AB=2AO=2,
∴∠AGO=60°,
∵GC=GA,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=2,MG=CG=1,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣GM=﹣1.
故答案为:﹣1.
12.解:当x=0时,y=2;当y=0时,x=4.
∴A(0,2),B(4,0).
∴OA=2,OB=4,
∴AB==2,
当⊙P在y轴上从下向上运动时⊙P与直线AB有两种相切情况.
第一种情况:如图,当⊙P在直线l:y=﹣x+2与y轴交点下方与直线l相切时,过P1作P1D1⊥l于D1,
在Rt△D1P1A中,D1P1=1.
∵Rt△D1P1A∽Rt△OBA,
∴=,
∴=,
∴AP1=,
∴OP1=OA﹣AP1=2﹣,
∴P1坐标为(0,2﹣);
第二种情况:如图,当⊙P在直线l:y=﹣x+2与y轴交点上方与直线AB相切时,过P2作P2D2⊥l轴于D2,
同上可得OP2=OA+AP2=2+,
∴P2点的坐标为(0,2+).
∴P点的坐标为(0,2﹣)或(0,2+).
故答案为:(0,2﹣)或(0,2+).
13.解:连结AO,并延长交⊙O于E,连结EC,延长BD交AC于F,
∵AE为直径,
∴∠ACE=∠ABE=90°,
∵点D是△ABC高线的交点,
∴BF⊥AC,AG⊥BC,CD⊥AB,
∴∠CFB=∠CGA=90°,
∴∠FDG=360°﹣90°﹣90°﹣60°=120°,
∴∠ADB=∠FDG=120°,
∵∠ACE=∠CFB=90°,CD⊥AB,EB⊥AB,
∴CE∥DB,CD∥EB,
∴四边形CDBE为平行四边形,
∴CD=BE,
∵=,
∴∠ACB=∠AEB=60°,
∴∠EAB=90°﹣∠AEB=90°﹣60°=30°,
在Rt△ABE中,
BE=AB×tan30°=8×=,
∴CD=BE=.
故答案为:120°;.
14.解:过点P作AP⊥EF交EF于点A,连接PE,设OP=x,
∵⊙P与x轴相切于原点O,
∴OP⊥OB,
∵平行于y轴的直线交⊙P于E,F两点,
∴四边形APOB是矩形,
∴AB=OP=x,
∵点E的坐标是(﹣3,﹣1),
∴AP=OB=3,AE=AB﹣BE=x﹣1,
在Rt△ABE中,32+(x﹣1)2=x2,
解得x=5,
∴AE=4,
∵AF=AE,
∴EF=8,
∴BF=EF+BE=9,
∴点F的坐标是(﹣3,﹣9).
故答案为(﹣3,﹣9).
15.解:∵AB=AC,
∴=,∠ABC=∠ACB,
∴∠ABC=∠ADB,∠ABC=(180°﹣∠BAC)=90°﹣∠BAC,
∵BD⊥AC,
∴∠ADB=90°﹣∠CAD,
∴∠BAC=∠CAD,
∴∠BAC=2∠CAD,故①正确,
∵DF=DC,
∴∠DFC=∠DCF,
∴∠BDC=2∠DFC,
∴∠BFC=∠BDC=∠BAC=∠FBC,
∴CB=CF,
又BD⊥AC,
∴AC是线段BF的中垂线,故②正确,
AB=AF=10,AC=10.
又BC=4,
设AE=x,CE=10﹣x,
由AB2﹣AE2=BC2﹣CE2,得100﹣x2=80﹣(10﹣x)2,
解得x=6,
∴AE=6,BE=8,CE=4,
∴DE===3,故③错误,
过点D作DH⊥AB于H.
∵∠DBH=∠ABE,∠BHD=∠AEB=90°,
∴△DBH∽△ABE,
∵==,
∴==,
∴BH=,DH=,
∴AH=AB﹣BH=10﹣=,
∴tan∠BAD===,故④正确.
故答案为:①②④.
16.解:连接OA,OF,设正方形ABCD的边长为a,正方形EFGD的边长为b,⊙O的半径为R.
则OB=,OG=,
而OC=BC﹣OB=OG﹣CG,
∴有:a﹣=﹣b得到:+=a+b,
两边平方得:R2﹣a2+2 +R2﹣b2=a2+2ab+b2
整理得: =a2+b2+ab﹣R2
两边再次平方得:R4﹣(a2+b2)R2+a2b2=(a2+b2+ab)2﹣2(a2+b2+ab)R2+R4,
整理得:a2+b2=R2=5,
∴阴影部分的面积=×π×5﹣5=π﹣5.
故答案为:π﹣5.
三.解答题(共5小题,满分40分)
17.(1)证明:连接OE.
在△OEF和△OEB中,
,
∴△OEF≌△OEB(SSS),
∴∠OFE=∠OBE,
∵OB=OD,
∴∠OBE=∠ODE,
∴∠OFE=∠ODE.
(2)∵AB是直径,
∴∠AFB=90°,
∵EF⊥BE,
∴∠BEF=90°,
∵EF=EB,
∴∠EFB=∠EFA=45°,
∵△OEF≌△OEB,
∴∠OEF=∠OEB=45°,
∴∠AFE=∠OEF=45°,
∴AF∥OE,
∵∠OFE=∠ODE,
∴∠FOH=∠DEF=90°,
∵OD⊥AC,
∴∠AOF=∠AHD=90°,
∴AO∥AE,
∴四边形AEOF是平行四边形,
∴OF=AE=5,AF=OE,
∵EH=1,
∴AH=AE﹣EH=4,
∴OH===3,
∴OE===,
∴AF=.
18.(1)证明:∵四边形ACDG是⊙O的内接四边形,
∴∠ACD+∠AGD=180°,
∵∠AGD+∠DGF=180°,
∴∠ACD=∠DGF,
∵CD⊥AB,AB为直径,
∴=,
∴∠AGC=∠ACD,
∴∠DGF=∠AGC.
(2)∵∠DGF=∠ACD,∠F=∠F,
∴△FDG∽△FAC,
∴=,
∴FD FC=FG FA,
∵CD⊥AB,
∴tanF==,
∵ED=DF,
∴EF=2DE,
∵==,
∴==,
∴∠ACD=60°,
∴∠CAE=30°,
∴AC=2CE,
设CE=DE=DF=x,则AE=x,AC=2x,FC=3x,
在Rt△AEF中,由勾股定理得AF==x,
∵FD FC=FA FG,
∴x 3x=6x,
解得x=0(舍)或x=2,
∴AC=2x=4.
19.(1)证明:延长BO交AC于H,连接OC,如图,
∵AD为直径,
∴∠ACD=90°,
∵BA=BC,OA=OC,
∴BH垂直平分AC,
∵BF为⊙O的切线,
∴BH⊥BF,
∴BF∥AC,
∴∠ACD+∠BFC=180°,
∴∠BFC=90°;
(2)解:∵BH⊥AC,∠ACD=90°,
∴BH∥CF,
∴∠BCD=∠HBC,
∵∠BCD=∠BAD,
∴∠HBC=∠BAD,
∴tan∠HBC=tan∠BAD=,
∵OA=OD,AH=CH,
∴OH=CD=1,
在Rt△BCH中,设⊙O的半径为r,
∵tan∠HBC==,
∴CH=(r+1),
在Rt△OCH中,12+(r+1)2=r2,解得r1=,r2=﹣1(舍去),
∴BO=,BH=,CH=,
在Rt△BCH中,BC===,
∵OB∥CD,
∴===,
∴=,
∴CE=CB=×=.
20.解:(1)∵DE为⊙O的直径,
∴∠EFD=90°,
∴DF⊥EF,
∵OG⊥EF,
∴OG∥CD,
∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∵AB∥OG,
∴四边形ABGO为平行四边形,
∵AO=AB,
∴四边形ABGO为菱形;
(2)如图,连接OB,过点O作OH⊥BC于点H,
∵四边形ABGO为菱形,
∴OB⊥AG,
∵⊙O和AG相切于点P.
∴OP⊥AG,
∴O,P,B三点共线,OP=OB,
∵∠D=∠OGH,AB=6,
∴BG=OG=6,
∴GH=OG cos∠OGH=6×=2,
由勾股定理,得OH==4,
∴OB==4.
∴⊙O的半径R为2.
21.解:(1)∵△ABC是等边三角形,
∴∠ABC=∠BAC=∠ACB=60°,
∵,,
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)证明:∵CM∥BP,
∴∠BPM+∠M=180°,
∠PCM=∠BPC,
∵∠BPC=∠BAC=60°,
∴∠PCM=∠BPC=60°,
∴∠M=180°﹣∠BPM=180°﹣(∠APC+∠BPC)=180°﹣120°=60°,
∴∠M=∠BPC=60°,
又∵A、P、B、C四点共圆,
∴∠PAC+∠PCB=180°,
∵∠MAC+∠PAC=180°
∴∠MAC=∠PBC
∵AC=BC,
在△ACM和△BCP中,
,
∴△ACM≌△BCP(AAS);
(3)∵CM∥BP,
∴四边形PBCM为梯形,
作PH⊥CM于H,
∵△ACM≌△BCP,
∴CM=CP,AM=BP,
又∠M=60°,
∴△PCM为等边三角形,
∴CM=CP=PM=PA+AM=PA+AMB=1+2=3,
在Rt△PMH中,∠MPH=30°,
∴PH=,
∴S四边形PBCM=(PB+CM)×PH=(2+3)×=;
(4)过点B作BQ⊥AP,交AP的延长线于点Q,过点A作AN⊥BC于点N,连接OB,
∵∠APC=∠BPC=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴PQ=PB=1,
在Rt△BPQ中,BQ=,
在Rt△AQB中,AB=,
∵△ABC为等边三角形,
∴AN经过圆心O,
∴BN=AB=,
∴AN=,
在Rt△BON中,设BO=x,则ON=,
∴,
解得:x=,
∵∠BOA=∠BCA=120°,
∴的长度为.
