2021-2022学年华东师大版八年级数学上册第14章 勾股定理 同步练习题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第14章 勾股定理 同步练习题 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-14 22:39:38 | ||
图片预览




文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》同步练习题(附答案)
1.已知三条线段的长是:①5k,12k,13k(k>0);②,,;③32,42,52;④11,60,61;⑤(m+1)2﹣1,2(m+1),(m+1)2+1.其中能够成直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
2.下列说法中不正确的是( )
A.三个内角度数之比为3:4:5的三角形是直角三角形
B.三边长之比为3:4:5的三角形是直角三角形
C.三个内角度数之比为1:2:3的三角形是直角三角形
D.三边长之比为1:2:的三角形是直角三角形
3.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
4.下列四组数中,不能构成直角三角形边长的一组是( )
A.0.3,0.4,0.5 B.6,8,10
C.52,122,132 D.1,,
5.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区.
A.10 B.7 C.6 D.12
6.如图,某公园内的一块草坪是长方形ABCD,已知AB=8m,BC=6m,公园管理处为了方便群众,沿AC修了一条近道,一个人从A到C走A﹣B﹣C比直接走AC多走了( )
A.2米 B.4米 C.6米 D.8米
7.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.6 B.8 C.9 D.15
8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
9.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
10.如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm的B处的食物,则蚂蚁经过的最短距离为( )
A.10cm B.12cm C.15cm D.8cm
11.美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
12.下列说法中,错误的是( )
A.在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形
B.在△ABC中,若∠A:∠B:∠C=3:4:5.则△ABC是直角三角形
C.在△ABC中,若∠A=∠B﹣∠C,则△ABC是直角三角形
D.在△ABC中,若三边长a,b,c满足a:b:c=1:2:,则△ABC是直角三角形
13.如图,由四个边长为2的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中AC边上的高是( )
A. B. C. D.
14.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是 .
15.如图,是一个3×3的魔方放在桌面上,该魔方上每一个小方格的边长都是2cm,其下底面点A处有一只蚂蚁,侧面点B处有一滴蜂蜜,若蚂蚁沿魔方的表面爬行从点A到点B去吃蜂蜜,则蚂蚁爬行的最短路径为 .
16.如图,所有的四边形都是正方形,所有的三角形都是直角三角形.则下列关于面积的等式:①SA=SB+SC;②SA=SF+SG+SB;③SB+SC=SD+SE+SF+SG,其中成立的有(写出序号即可) .
17.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 .
18.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.
19.如图是一个三级台阶,它的每一级的长、宽、高分别是3米、0.3米、0.2米,A,B是这个台阶上两个相对的端点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是 米.
20.如图,长方体的长为15cm,宽为10cm,高为20cm,BC=5cm,一只蚂蚁如果沿着长方体的表面从点A爬到点B,求蚂蚁需要爬行的最短距离.
21.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
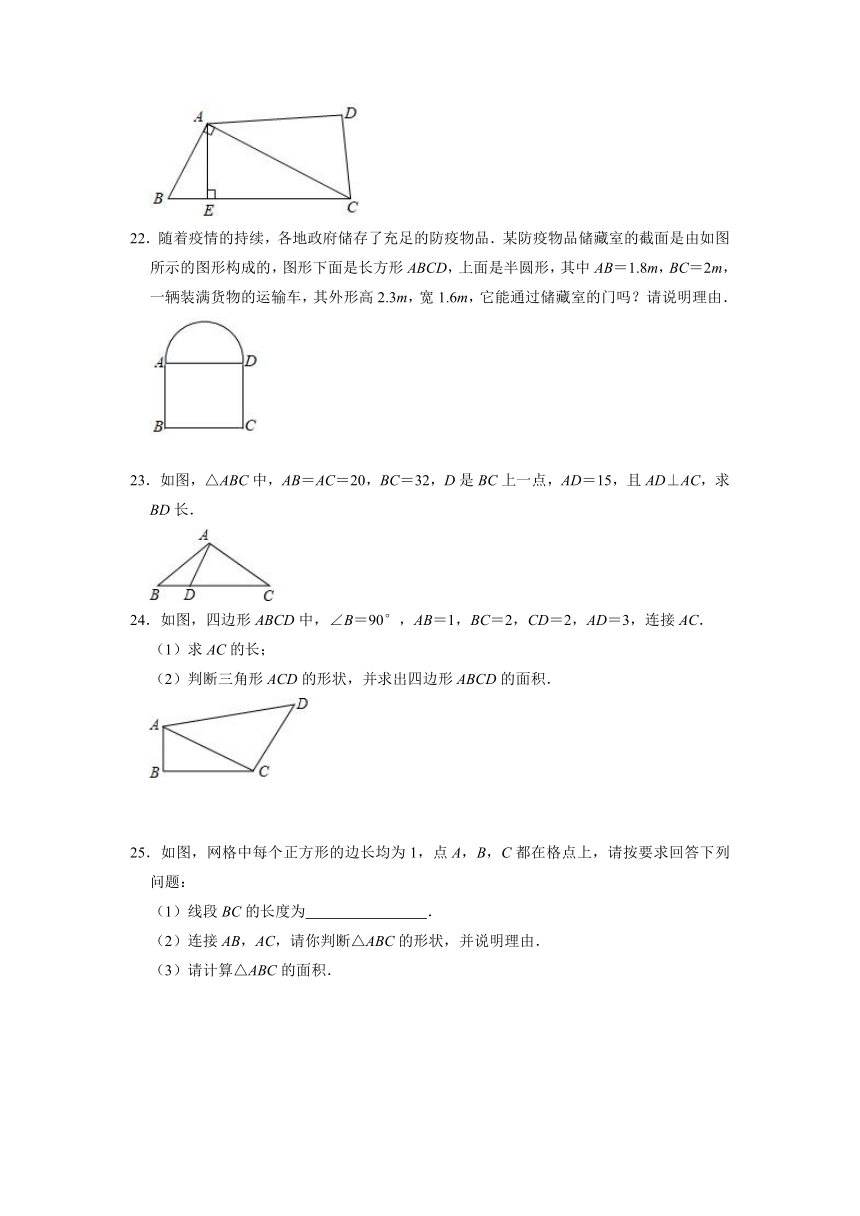
22.随着疫情的持续,各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的,图形下面是长方形ABCD,上面是半圆形,其中AB=1.8m,BC=2m,一辆装满货物的运输车,其外形高2.3m,宽1.6m,它能通过储藏室的门吗?请说明理由.
23.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
24.如图,四边形ABCD中,∠B=90°,AB=1,BC=2,CD=2,AD=3,连接AC.
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
25.如图,网格中每个正方形的边长均为1,点A,B,C都在格点上,请按要求回答下列问题:
(1)线段BC的长度为 .
(2)连接AB,AC,请你判断△ABC的形状,并说明理由.
(3)请计算△ABC的面积.
26.如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.求四边形ABDC的面积.
参考答案
1.解:①∵(5k)2+(12k)2=(13k)2,∴能够成直角三角形;
②∵()2+()2≠()2,∴不能够成直角三角形;
③∵(32)2+(42)2≠(52)2,∴不能够成直角三角形;
④∵112+602=612,∴能够成直角三角形;
⑤∵[(m+1)2﹣1]2+[2(m+1)]2=[(m+1)2+1]2,∴能够成直角三角形;
故选:B.
2.解:A、∵三角形三个内角度数之比为3:4:5,
∴设三角形的三个内角分别为3x,4x,5x,则3x+4x+5x=180°,
解得x=15°,
∴5x=75°,
∴该三角形不是直角三角形,故本选项错误;
B、∵三条边长之比为3:4:5,
设三角形的三边分别为:3k,4k,5k,
∵(3k)2+(4k)2=(5k)2,
∴该三角形是直角三角形,故B选项正确;
C、三角形的最大角=180°×=90°,
所以三角形是直角三角形,故本选项正确;
D、∵三边长之比为1:2:,
∴设三角形的三边分别为:k,2k,k,
∵k2+(k)2=(2k)2,
∴该三角形是直角三角形,故D选项正确.
故选:A.
3.解:化简(a+b)2=c2+2ab,得,a2+b2=c2所以三角形是直角三角形,
故选:C.
4.解:A.∵0.32+0.42=0.52,
∴以0.3,0.4,0.5为边能组成直角三角形,故本选项不符合题意;
B.∵62+82=102,
∴以6,8,10为边能组成直角三角形,故本选项不符合题意;
C.∵(52)2+(122)2≠(132)2,
∴以52,122,132为边不能组成直角三角形,故本选项符合题意;
D.∵12+()2=()2,
∴以1,,为边能组成直角三角形,故本选项不符合题意;
故选:C.
5.解:如图所示:设x小时后,就进入台风影响区,根据题意得出:
CE=40x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400(km),
∴AE=400﹣40x,AB′=300﹣20x,
∴AE2+AB′2=EB′2,
即(400﹣40x)2+(300﹣20x)2=2002,
解得:x1=15,x2=7,
∴轮船经7小时就进入台风影响区.
故选:B.
6.解:由勾股定理,得
捷径AC==10(m),
多走了8+6﹣10=4(m).
故选:B.
7.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
答:蚂蚁爬行的最短线路为15.
故选:D.
8.解:由题意,
①﹣②得2xy=45 ③,
∴2xy+4=49,
①+③得x2+2xy+y2=94,
∴(x+y)2=94,
∴①②③正确,④错误.
故选:B.
9.解:设小正方形的边长为1,
则AB2=22+22=8,CD2=22+42=20,
EF2=12+22=5,GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
10.解:如图,将圆柱的侧面展开,蚂蚁经过的最短距离为线段AB的长.
由勾股定理,AB2=AC2+BC2=82+(8﹣1﹣1)2=100,
AB=10cm.
故选:A.
11.解:根据勾股定理可得:S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选:B.
12.解:A、在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形,可得∠A=180°÷(1++)=90°,是直角三角形,不符合题意;
B、在△ABC中,若∠A:∠B:∠C=3:4:5,可得∠C=180°×=75°,不是直角三角形,符合题意;
C、在△ABC中,若∠A=∠B﹣∠C,则∠B=90°,则△ABC是直角三角形,不符合题意;
D、12+()2=22,是直角三角形,不符合题意.
故选:B.
13.解:作BD⊥AC于D,如图所示:
∵小正方形的边长为2,
∴AC==,
∵S△ABC=4×4﹣×2×2﹣×2×4﹣×2×4=6,
∴S△ABC=×AC×BD=×2×BD=6,
解得:BD=.
故选:D.
14.解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD===9,
在Rt△ACD中,
CD===5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD===9,
在Rt△ACD中,CD===5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故填:42或32.
15.解:如图1,把我们所看到的前面和上面组成一个平面,
AB==4(cm);
如图2,把我们所看到的前面和,右面组成一个平面,
AB==2(cm),
∵4>2,
∴蚂蚁爬行的最短路径为2(cm),
故答案为:2cm.
16.解:由勾股定理和正方形的性质可知:SA=SB+SC,SB=SD+SE,SC=SF+SG,
∴SA=SB+SC=SF+SG+SB,SB+SC=SD+SE+SF+SG,
故答案为:①②③.
17.解:S1=π()2=πAC2,S2=πBC2,
所以S1+S2=π(AC2+BC2)=πAB2=2π.
故答案为:2π.
18.解:①如图1,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠ACG=90°,AC=12+9=21,CG=5,
在Rt△ACG中,由勾股定理得:AG==(cm);
②如图2,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠ABG=90°,AB=12,BG=9+5=14,
在Rt△ACBG中,由勾股定理得:AG===2(cm);
③如图3,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠AFG=90°,AF=5+12=17,FG=9,
在Rt△AFG中,由勾股定理得:AG==(cm).
∴蚂蚁爬行的最短路程是2cm,
故答案为:2.
19.解:三级台阶平面展开图为长方形,长为3,宽为(0.2+0.3)×3,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到B点最短路程为x,
由勾股定理得:x2=32+[(0.2+0.3)×3]2=11.25,
解得x=(米),
答:蚂蚁沿台阶面爬行到B点最短路程是米,
故答案为:.
20.解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===25cm;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5cm;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB===5cm;
∵25<5<5,
∴蚂蚁爬行的最短距离是25cm.
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC===15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACD=AB×AC+AD×CD=×8×15+×12×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABC=BC×AE=AB AC,
∴17×AE=8×15,
解得:AE=(m),
即小路AE的长为m.
22.解:能通过;
理由:由题意得,运输车从中间过更容易通过储藏室,能通过的最大高度为EF的长度,
如图,设点O为半圆的圆心,点P为运输车的外边沿,
则OP=0.8m,OE=1m,∠OPE=90°,
在Rt△OPE中,由勾股定理得,EP2=OE2﹣OP2=1﹣0.82=0.36,
∴EP=0.6(m),
∴EF=0.6+1.8=2.4(m),
∵2.4>2.3,
∴运输车通过储藏室的门.
23.解:∵AD⊥AC,AC=20,AD=15,
∴CD==25
∴BD=BC﹣CD=32﹣25=7.
24.解:(1)∵∠B=90°,AB=2,BC=1,
∴AC2=AB2+BC2=4+1=5,
∴AC=;
(2)∵△ACD中,AC=,CD=2,AD=3,
∴AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴四边形ABCD的面积=1×2+2×=1+.
25.解:(1)BC=;
故答案为:5;
(2)△ABC是直角三角形,
∵AB2=12+32=10,AC2=22+62=40,
∴AB2+AC2=10+40=50=BC2,
∴△ABC是直角三角形;
(3)由(2)得,AB=,AC=2,∠BAC=90°,
∴△ABC的面积为:.
26.解:∵∠A=90°,AB=9,AC=12,
∴BC===15,
∵BC=15,BD=8,CD=17,
∴BC2+BD2=CD2,
∴△BCD是直角三角形,
∴S四边形ABCD=S△BCD+S△ABC=×15×8+×9×12=114.
1.已知三条线段的长是:①5k,12k,13k(k>0);②,,;③32,42,52;④11,60,61;⑤(m+1)2﹣1,2(m+1),(m+1)2+1.其中能够成直角三角形的有( )
A.2个 B.3个 C.4个 D.5个
2.下列说法中不正确的是( )
A.三个内角度数之比为3:4:5的三角形是直角三角形
B.三边长之比为3:4:5的三角形是直角三角形
C.三个内角度数之比为1:2:3的三角形是直角三角形
D.三边长之比为1:2:的三角形是直角三角形
3.三角形的三边长为a,b,c,且满足(a+b)2=c2+2ab,则这个三角形是( )
A.等边三角形 B.钝角三角形 C.直角三角形 D.锐角三角形
4.下列四组数中,不能构成直角三角形边长的一组是( )
A.0.3,0.4,0.5 B.6,8,10
C.52,122,132 D.1,,
5.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区.
A.10 B.7 C.6 D.12
6.如图,某公园内的一块草坪是长方形ABCD,已知AB=8m,BC=6m,公园管理处为了方便群众,沿AC修了一条近道,一个人从A到C走A﹣B﹣C比直接走AC多走了( )
A.2米 B.4米 C.6米 D.8米
7.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则这只蚂蚁沿着台阶面爬行的最短路程是( )
A.6 B.8 C.9 D.15
8.如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
9.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A.CD、EF、GH B.AB、EF、GH C.AB、CD、GH D.AB、CD、EF
10.如图,有一圆柱,其高为8cm,它的底面周长为16cm,在圆柱外侧距下底1cm的A处有一只蚂蚁,它想得到距上底1cm的B处的食物,则蚂蚁经过的最短距离为( )
A.10cm B.12cm C.15cm D.8cm
11.美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.S△EDA=S△CEB B.S△EDA+S△CDE+S△CEB=S四边形ABCD
C.S△EDA+S△CEB=S△CDE D.S四边形AECD=S四边形DEBC
12.下列说法中,错误的是( )
A.在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形
B.在△ABC中,若∠A:∠B:∠C=3:4:5.则△ABC是直角三角形
C.在△ABC中,若∠A=∠B﹣∠C,则△ABC是直角三角形
D.在△ABC中,若三边长a,b,c满足a:b:c=1:2:,则△ABC是直角三角形
13.如图,由四个边长为2的小正方形构成一个大正方形,连接小正方形的三个顶点,可得到△ABC,则△ABC中AC边上的高是( )
A. B. C. D.
14.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是 .
15.如图,是一个3×3的魔方放在桌面上,该魔方上每一个小方格的边长都是2cm,其下底面点A处有一只蚂蚁,侧面点B处有一滴蜂蜜,若蚂蚁沿魔方的表面爬行从点A到点B去吃蜂蜜,则蚂蚁爬行的最短路径为 .
16.如图,所有的四边形都是正方形,所有的三角形都是直角三角形.则下列关于面积的等式:①SA=SB+SC;②SA=SF+SG+SB;③SB+SC=SD+SE+SF+SG,其中成立的有(写出序号即可) .
17.如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 .
18.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.
19.如图是一个三级台阶,它的每一级的长、宽、高分别是3米、0.3米、0.2米,A,B是这个台阶上两个相对的端点,A点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是 米.
20.如图,长方体的长为15cm,宽为10cm,高为20cm,BC=5cm,一只蚂蚁如果沿着长方体的表面从点A爬到点B,求蚂蚁需要爬行的最短距离.
21.如图,学校操场边有一块四边形空地ABCD,其中AB⊥AC,AB=8m,BC=17m,CD=9m,AD=12m.为了美化校园环境,创建绿色校园,学校计划将这块四边形空地进行绿化整理.
(1)求需要绿化的空地ABCD的面积;
(2)为方便师生出入,设计了过点A的小路AE,且AE⊥BC于点E,试求小路AE的长.
22.随着疫情的持续,各地政府储存了充足的防疫物品.某防疫物品储藏室的截面是由如图所示的图形构成的,图形下面是长方形ABCD,上面是半圆形,其中AB=1.8m,BC=2m,一辆装满货物的运输车,其外形高2.3m,宽1.6m,它能通过储藏室的门吗?请说明理由.
23.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
24.如图,四边形ABCD中,∠B=90°,AB=1,BC=2,CD=2,AD=3,连接AC.
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
25.如图,网格中每个正方形的边长均为1,点A,B,C都在格点上,请按要求回答下列问题:
(1)线段BC的长度为 .
(2)连接AB,AC,请你判断△ABC的形状,并说明理由.
(3)请计算△ABC的面积.
26.如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.求四边形ABDC的面积.
参考答案
1.解:①∵(5k)2+(12k)2=(13k)2,∴能够成直角三角形;
②∵()2+()2≠()2,∴不能够成直角三角形;
③∵(32)2+(42)2≠(52)2,∴不能够成直角三角形;
④∵112+602=612,∴能够成直角三角形;
⑤∵[(m+1)2﹣1]2+[2(m+1)]2=[(m+1)2+1]2,∴能够成直角三角形;
故选:B.
2.解:A、∵三角形三个内角度数之比为3:4:5,
∴设三角形的三个内角分别为3x,4x,5x,则3x+4x+5x=180°,
解得x=15°,
∴5x=75°,
∴该三角形不是直角三角形,故本选项错误;
B、∵三条边长之比为3:4:5,
设三角形的三边分别为:3k,4k,5k,
∵(3k)2+(4k)2=(5k)2,
∴该三角形是直角三角形,故B选项正确;
C、三角形的最大角=180°×=90°,
所以三角形是直角三角形,故本选项正确;
D、∵三边长之比为1:2:,
∴设三角形的三边分别为:k,2k,k,
∵k2+(k)2=(2k)2,
∴该三角形是直角三角形,故D选项正确.
故选:A.
3.解:化简(a+b)2=c2+2ab,得,a2+b2=c2所以三角形是直角三角形,
故选:C.
4.解:A.∵0.32+0.42=0.52,
∴以0.3,0.4,0.5为边能组成直角三角形,故本选项不符合题意;
B.∵62+82=102,
∴以6,8,10为边能组成直角三角形,故本选项不符合题意;
C.∵(52)2+(122)2≠(132)2,
∴以52,122,132为边不能组成直角三角形,故本选项符合题意;
D.∵12+()2=()2,
∴以1,,为边能组成直角三角形,故本选项不符合题意;
故选:C.
5.解:如图所示:设x小时后,就进入台风影响区,根据题意得出:
CE=40x千米,BB′=20x千米,
∵BC=500km,AB=300km,
∴AC=400(km),
∴AE=400﹣40x,AB′=300﹣20x,
∴AE2+AB′2=EB′2,
即(400﹣40x)2+(300﹣20x)2=2002,
解得:x1=15,x2=7,
∴轮船经7小时就进入台风影响区.
故选:B.
6.解:由勾股定理,得
捷径AC==10(m),
多走了8+6﹣10=4(m).
故选:B.
7.解:将台阶展开,如图,
因为AC=3×3+1×3=12,BC=9,
所以AB2=AC2+BC2=225,
所以AB=15,
所以蚂蚁爬行的最短线路为15.
答:蚂蚁爬行的最短线路为15.
故选:D.
8.解:由题意,
①﹣②得2xy=45 ③,
∴2xy+4=49,
①+③得x2+2xy+y2=94,
∴(x+y)2=94,
∴①②③正确,④错误.
故选:B.
9.解:设小正方形的边长为1,
则AB2=22+22=8,CD2=22+42=20,
EF2=12+22=5,GH2=22+32=13.
因为AB2+EF2=GH2,
所以能构成一个直角三角形三边的线段是AB、EF、GH.
故选:B.
10.解:如图,将圆柱的侧面展开,蚂蚁经过的最短距离为线段AB的长.
由勾股定理,AB2=AC2+BC2=82+(8﹣1﹣1)2=100,
AB=10cm.
故选:A.
11.解:根据勾股定理可得:S△EDA+S△CDE+S△CEB=S四边形ABCD.
故选:B.
12.解:A、在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形,可得∠A=180°÷(1++)=90°,是直角三角形,不符合题意;
B、在△ABC中,若∠A:∠B:∠C=3:4:5,可得∠C=180°×=75°,不是直角三角形,符合题意;
C、在△ABC中,若∠A=∠B﹣∠C,则∠B=90°,则△ABC是直角三角形,不符合题意;
D、12+()2=22,是直角三角形,不符合题意.
故选:B.
13.解:作BD⊥AC于D,如图所示:
∵小正方形的边长为2,
∴AC==,
∵S△ABC=4×4﹣×2×2﹣×2×4﹣×2×4=6,
∴S△ABC=×AC×BD=×2×BD=6,
解得:BD=.
故选:D.
14.解:此题应分两种情况说明:
(1)当△ABC为锐角三角形时,在Rt△ABD中,
BD===9,
在Rt△ACD中,
CD===5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD===9,
在Rt△ACD中,CD===5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
综上所述,△ABC的周长是42或32.
故填:42或32.
15.解:如图1,把我们所看到的前面和上面组成一个平面,
AB==4(cm);
如图2,把我们所看到的前面和,右面组成一个平面,
AB==2(cm),
∵4>2,
∴蚂蚁爬行的最短路径为2(cm),
故答案为:2cm.
16.解:由勾股定理和正方形的性质可知:SA=SB+SC,SB=SD+SE,SC=SF+SG,
∴SA=SB+SC=SF+SG+SB,SB+SC=SD+SE+SF+SG,
故答案为:①②③.
17.解:S1=π()2=πAC2,S2=πBC2,
所以S1+S2=π(AC2+BC2)=πAB2=2π.
故答案为:2π.
18.解:①如图1,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠ACG=90°,AC=12+9=21,CG=5,
在Rt△ACG中,由勾股定理得:AG==(cm);
②如图2,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠ABG=90°,AB=12,BG=9+5=14,
在Rt△ACBG中,由勾股定理得:AG===2(cm);
③如图3,展开后连接AG,则AG就是在表面上A到G的最短距离,
∵∠AFG=90°,AF=5+12=17,FG=9,
在Rt△AFG中,由勾股定理得:AG==(cm).
∴蚂蚁爬行的最短路程是2cm,
故答案为:2.
19.解:三级台阶平面展开图为长方形,长为3,宽为(0.2+0.3)×3,
则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.
可设蚂蚁沿台阶面爬行到B点最短路程为x,
由勾股定理得:x2=32+[(0.2+0.3)×3]2=11.25,
解得x=(米),
答:蚂蚁沿台阶面爬行到B点最短路程是米,
故答案为:.
20.解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===25cm;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB===5cm;
只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB===5cm;
∵25<5<5,
∴蚂蚁爬行的最短距离是25cm.
21.解:(1)∵AB⊥AC,
∴∠BAC=90°,
∴AC===15(m),
∵CD=9m,AD=12m,
∴AD2+CD2=122+92=225=AC2,
∴△ACD是直角三角形,∠D=90°,
∴需要绿化的空地ABCD的面积=S△ABC+S△ACD=AB×AC+AD×CD=×8×15+×12×9=114(m2);
(2)∵∠BAC=90°,AE⊥BC,
∴S△ABC=BC×AE=AB AC,
∴17×AE=8×15,
解得:AE=(m),
即小路AE的长为m.
22.解:能通过;
理由:由题意得,运输车从中间过更容易通过储藏室,能通过的最大高度为EF的长度,
如图,设点O为半圆的圆心,点P为运输车的外边沿,
则OP=0.8m,OE=1m,∠OPE=90°,
在Rt△OPE中,由勾股定理得,EP2=OE2﹣OP2=1﹣0.82=0.36,
∴EP=0.6(m),
∴EF=0.6+1.8=2.4(m),
∵2.4>2.3,
∴运输车通过储藏室的门.
23.解:∵AD⊥AC,AC=20,AD=15,
∴CD==25
∴BD=BC﹣CD=32﹣25=7.
24.解:(1)∵∠B=90°,AB=2,BC=1,
∴AC2=AB2+BC2=4+1=5,
∴AC=;
(2)∵△ACD中,AC=,CD=2,AD=3,
∴AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴△ACD是直角三角形,
∴四边形ABCD的面积=1×2+2×=1+.
25.解:(1)BC=;
故答案为:5;
(2)△ABC是直角三角形,
∵AB2=12+32=10,AC2=22+62=40,
∴AB2+AC2=10+40=50=BC2,
∴△ABC是直角三角形;
(3)由(2)得,AB=,AC=2,∠BAC=90°,
∴△ABC的面积为:.
26.解:∵∠A=90°,AB=9,AC=12,
∴BC===15,
∵BC=15,BD=8,CD=17,
∴BC2+BD2=CD2,
∴△BCD是直角三角形,
∴S四边形ABCD=S△BCD+S△ABC=×15×8+×9×12=114.
