2021 2022学年人教版数学七年级上册专题09 1.4 有理数的乘除法 -期末考复习专题训练(word版 含答案)
文档属性
| 名称 | 2021 2022学年人教版数学七年级上册专题09 1.4 有理数的乘除法 -期末考复习专题训练(word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 272.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览


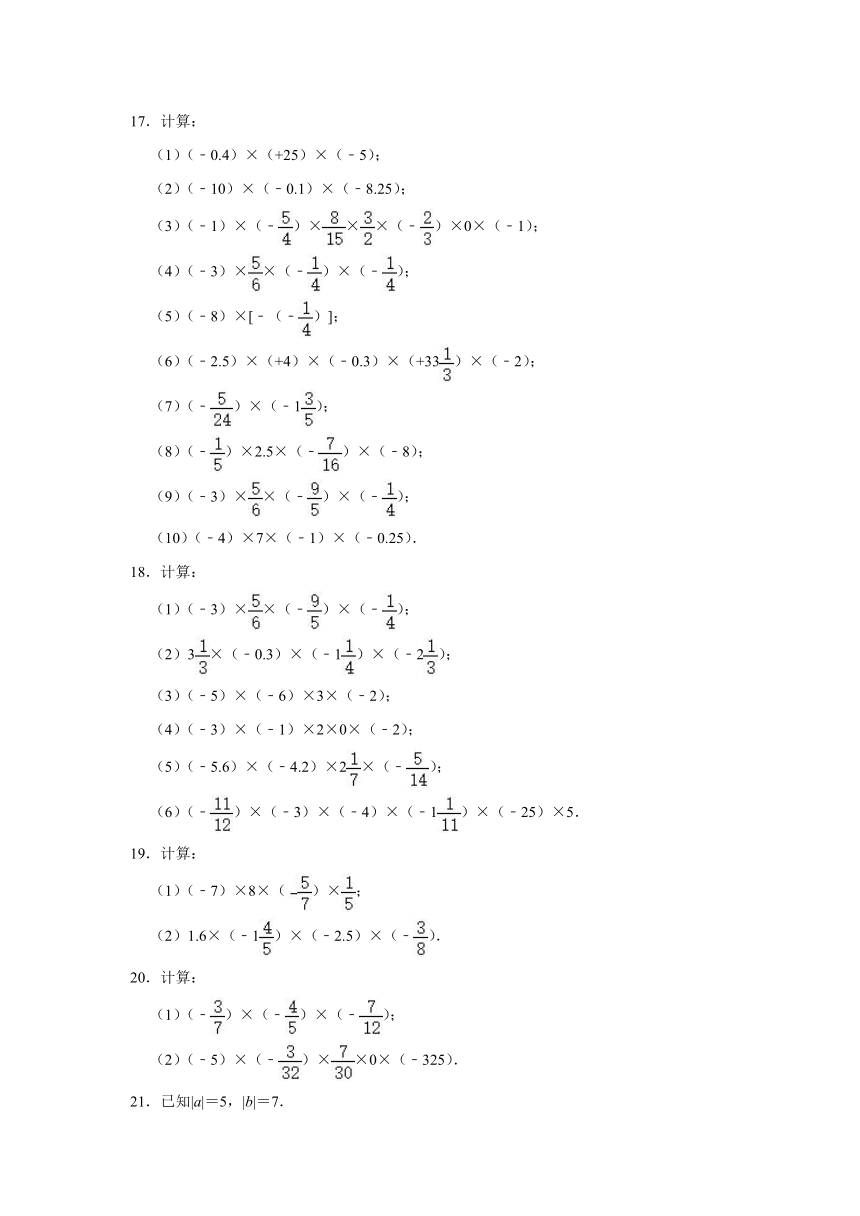


文档简介
专题09 : 2021年人教新版七年级(上册)1.4 有理数的乘除法 -期末考复习专题训练
一.选择题(共7小题)
1.计算(﹣9)×的结果是( )
A.3 B.27 C.﹣27 D.﹣3
2.若数a的相反数的倒数为1,则数a是( )
A. B. C. D.
3.下列计算正确的个数有( )
①(﹣6)×(﹣5)=﹣30;
②(﹣4)×3=﹣12;
③(﹣6)×0=﹣6;
④×=﹣1.
A.1个 B.2个 C.3个 D.4个
4.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0
B.a<0,b>0
C.a、b同号
D.a、b异号,且正数的绝对值较大
5.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则的值为( )
A. B.99! C.9900 D.2!
6.已知a=(﹣12)×(﹣23)×(﹣34)×(﹣45),b=(﹣123)×(﹣234)×(﹣345),判断下列叙述何者正确?( )
A.a,b皆为正数 B.a,b皆为负数
C.a为正数,b为负数 D.a为负数,b为正数
7.在下面五个说法中正确的有( )
①互为相反数的两个数的绝对值相等
②没有最大的整数,最大的负整数是﹣1,最小的正数是1
③一个数的相反数等于它本身,这个数是0
④任何有理数的绝对值都是正数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
8.已知|a|=4,|b|=2,那么ab= .
9.若a<c<0<b,则a×b×c 0.(用“>”“=”“<”填空)
10.已知4个不相等的整数a、b、c、d,它们的积abcd=25,则a+b+c+d= .
11.在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,所得的积最大为a,再取三个数所得的积最小为b,则a+b= .
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为5,则x2+(a+b)2018+(﹣cd)2017的值为 .
13.已知a是不等于﹣1的数,我们把称为a的和倒数.如:2的和倒数为=,已知a1=1,a2是a1的和倒数,a3是a2的和倒数.a4是a3的和倒数,…,依此类推,则a1 a2 a3…a10= .
14.若a、b、c是非零有理数,a+b+c=0,则++﹣的值为 .
三.解答题(共8小题)
15.计算:
(1)(﹣0.12)×(﹣0.25);
(2)×(﹣);
(3)(﹣1)×.
16.计算:
(1)(﹣2)×(﹣8)×(+5)×(﹣);
(2)(﹣0.25)×(﹣)×5×(﹣7);
(3)(﹣3)×(+)×(﹣1)×(﹣)×(+1);
(4)(﹣0.25)×(﹣7)×32×0.125×(﹣)×0.
17.计算:
(1)(﹣0.4)×(+25)×(﹣5);
(2)(﹣10)×(﹣0.1)×(﹣8.25);
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1);
(4)(﹣3)××(﹣)×(﹣);
(5)(﹣8)×[﹣(﹣)];
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2);
(7)(﹣)×(﹣1);
(8)(﹣)×2.5×(﹣)×(﹣8);
(9)(﹣3)××(﹣)×(﹣);
(10)(﹣4)×7×(﹣1)×(﹣0.25).
18.计算:
(1)(﹣3)××(﹣)×(﹣);
(2)3×(﹣0.3)×(﹣1)×(﹣2);
(3)(﹣5)×(﹣6)×3×(﹣2);
(4)(﹣3)×(﹣1)×2×0×(﹣2);
(5)(﹣5.6)×(﹣4.2)×2×(﹣);
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5.
19.计算:
(1)(﹣7)×8×()×;
(2)1.6×(﹣1)×(﹣2.5)×(﹣).
20.计算:
(1)(﹣)×(﹣)×(﹣);
(2)(﹣5)×(﹣)××0×(﹣325).
21.已知|a|=5,|b|=7.
(1)若ab<0,求|a﹣b|的值.
(2)若|a﹣b|=﹣(a﹣b),求a b的值.
22.设a、b、c为非零有理数|a|+a=0,|ab|=ab,|c|﹣c=0.化简:|b|﹣|a+b|﹣|c﹣b|+|a﹣c|.
专题09 : 2021年人教新版七年级(上册)1.4 有理数的乘除法 -期末考复习专题训练
参考答案与试题解析
一.选择题(共7小题)
1.计算(﹣9)×的结果是( )
A.3 B.27 C.﹣27 D.﹣3
【解答】解:原式=﹣(9×)=﹣3,
故选:D.
2.若数a的相反数的倒数为1,则数a是( )
A. B. C. D.
【解答】解:数a的相反数是﹣a,﹣a的倒数是﹣,
所以﹣=1,
所以a=﹣.
故选:C.
3.下列计算正确的个数有( )
①(﹣6)×(﹣5)=﹣30;
②(﹣4)×3=﹣12;
③(﹣6)×0=﹣6;
④×=﹣1.
A.1个 B.2个 C.3个 D.4个
【解答】解:①(﹣6)×(﹣5)=30;故①不合题意;
②(﹣4)×3=﹣12;故②符合题意;
③(﹣6)×0=0;,故③不合题意;
④×(﹣)=﹣1,故④合题意;
∴正确的有两个,
故选:B.
4.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0
B.a<0,b>0
C.a、b同号
D.a、b异号,且正数的绝对值较大
【解答】解:∵ab<0,
∴a,b异号,
∵a+b>0,
∴正数的绝对值较大,
故选:D.
5.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则的值为( )
A. B.99! C.9900 D.2!
【解答】解:原式=
=99×100
=9900.
故选:C.
6.已知a=(﹣12)×(﹣23)×(﹣34)×(﹣45),b=(﹣123)×(﹣234)×(﹣345),判断下列叙述何者正确?( )
A.a,b皆为正数 B.a,b皆为负数
C.a为正数,b为负数 D.a为负数,b为正数
【解答】解:∵a=(﹣12)×(﹣23)×(﹣34)×(﹣45)中共有4个负数相乘,
∴a为正数,
∵b=(﹣123)×(﹣234)×(﹣345)中共有3个负数相乘,
∴b为负数,
∴a为正数,b为负数,
故选:C.
7.在下面五个说法中正确的有( )
①互为相反数的两个数的绝对值相等
②没有最大的整数,最大的负整数是﹣1,最小的正数是1
③一个数的相反数等于它本身,这个数是0
④任何有理数的绝对值都是正数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
A.1个 B.2个 C.3个 D.4个
【解答】解:互为相反数的两个数的绝对值相等,故①正确,
没有最大的整数,最大的负整数是﹣1,最小的正数也没有,故②错误,
一个数的相反数等于它本身,这个数是0,故③正确,
任何有理数的绝对值都是非负数,故④错误,
几个不为零的有理数相乘,如果负因数有奇数个,则积为负数,故⑤错误,
故选:B.
二.填空题(共7小题)
8.已知|a|=4,|b|=2,那么ab= 8或﹣8 .
【解答】解:∵|a|=4,|b|=2,
∴a=±4,b=±2,
∴a=4,b=2时,ab=4×2=8;
当a=4,b=﹣2时,ab=4×(﹣2)=﹣8.
当a=﹣4,b=2时,ab=(﹣4)×2=﹣8.
当a=﹣4,b=﹣2时,ab=(﹣4)×(﹣2)=8.
∴ab的值为8或﹣8.
故答案为:8或﹣8.
9.若a<c<0<b,则a×b×c > 0.(用“>”“=”“<”填空)
【解答】解:∵a<c<0<b,
∴a,c为负数,b为正数,
∴a×c>0,
∴a×b×c>0.
故答案为>.
10.已知4个不相等的整数a、b、c、d,它们的积abcd=25,则a+b+c+d= 0 .
【解答】解:∵a、b、c、d是4个不相等的整数,
∴25=1×5×(﹣1)×(﹣5),
∴a+b+c+d=1+5+(﹣1)+(﹣5)=0;
故答案为0.
11.在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,所得的积最大为a,再取三个数所得的积最小为b,则a+b= ﹣24 .
【解答】解:在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,一共有四种情况:
①(﹣2)×3×4=﹣24,
②(﹣2)×3×(﹣6)=36,
③(﹣2)×4×(﹣6)=48,
④3×4×(﹣6)=﹣72,
∵所得的积最大为a,再取三个数所得的积最小为b,
∴a=48,b=﹣72,
∴a+b=﹣24,
故答案为:﹣24.
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为5,则x2+(a+b)2018+(﹣cd)2017的值为 24 .
【解答】解:根据题中的新定义化简得:a+b=0,cd=1,x=5或﹣5,
则原式=25+0﹣1=24.
故答案为:24.
13.已知a是不等于﹣1的数,我们把称为a的和倒数.如:2的和倒数为=,已知a1=1,a2是a1的和倒数,a3是a2的和倒数.a4是a3的和倒数,…,依此类推,则a1 a2 a3…a10= .
【解答】解:a1=1,a2=,a3==,,,,,,,,
则a1 a2 a3…a10=1×=.
故答案为:.
14.若a、b、c是非零有理数,a+b+c=0,则++﹣的值为 ﹣3或3 .
【解答】解:∵a、b、c是非零有理数,a+b+c=0,
∴当a、b、c中一正两负时,
不妨设a>0,b<0,c<0,则a=﹣(b+c),
故++﹣=1+(﹣1)+(﹣1)﹣2=﹣3;
当a、b、c中两正一负时,
不妨设a>0,b>0,c<0,则c=﹣(a+b),
故++﹣=1+1+(﹣1)+2=3;
故答案为:﹣3或3.
三.解答题(共8小题)
15.计算:
(1)(﹣0.12)×(﹣0.25);
(2)×(﹣);
(3)(﹣1)×.
【解答】解:(1)(﹣0.12)×(﹣0.25)
=
=0.03;
(2)
=
=;
(3)
=
=﹣1.
16.计算:
(1)(﹣2)×(﹣8)×(+5)×(﹣);
(2)(﹣0.25)×(﹣)×5×(﹣7);
(3)(﹣3)×(+)×(﹣1)×(﹣)×(+1);
(4)(﹣0.25)×(﹣7)×32×0.125×(﹣)×0.
【解答】解:(1)(﹣2)×(﹣8)×(+5)×(﹣),
=16×(﹣)
=;
(2)(﹣0.25)×()×5×(﹣7),
=(﹣0.25)×5×[(﹣)×(﹣7)],
=﹣×4,
=﹣5;
(3),
=,
=;
(4)
=0.
17.计算:
(1)(﹣0.4)×(+25)×(﹣5);
(2)(﹣10)×(﹣0.1)×(﹣8.25);
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1);
(4)(﹣3)××(﹣)×(﹣);
(5)(﹣8)×[﹣(﹣)];
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2);
(7)(﹣)×(﹣1);
(8)(﹣)×2.5×(﹣)×(﹣8);
(9)(﹣3)××(﹣)×(﹣);
(10)(﹣4)×7×(﹣1)×(﹣0.25).
【解答】解:(1)(﹣0.4)×(+25)×(﹣5)
=+(0.4×25×5)
=50;
(2)(﹣10)×(﹣0.1)×(﹣8.25)
=﹣(10×0.1×8.25)
=﹣8.25;
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1)
=0;
(4)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(5)(﹣8)×[﹣(﹣)]
=(﹣8)×
=﹣2;
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2)
=﹣(2.5×4)×(0.3×)×2
=﹣10×10×2
=﹣200;
(7)(﹣)×(﹣1)
=×
=;
(8)(﹣)×2.5×(﹣)×(﹣8)
=﹣(×2.5)×(×8)
=﹣×
=﹣;
(9)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(10)(﹣4)×7×(﹣1)×(﹣0.25)
=﹣(4×0.25×7×1)
=﹣7.
18.计算:
(1)(﹣3)××(﹣)×(﹣);
(2)3×(﹣0.3)×(﹣1)×(﹣2);
(3)(﹣5)×(﹣6)×3×(﹣2);
(4)(﹣3)×(﹣1)×2×0×(﹣2);
(5)(﹣5.6)×(﹣4.2)×2×(﹣);
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5.
【解答】解:(1)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(2)3×(﹣0.3)×(﹣1)×(﹣2)
=﹣×××
=﹣;
(3)(﹣5)×(﹣6)×3×(﹣2)
=﹣5×6×3×2
=﹣180;
(4)(﹣3)×(﹣1)×2×0×(﹣2)
=0;
(5)(﹣5.6)×(﹣4.2)×2×(﹣)
=﹣(5.6×4.2××)
=﹣18;
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5
=﹣××(4×25)×3×5
=﹣1×100×15
=﹣1500.
19.计算:
(1)(﹣7)×8×()×;
(2)1.6×(﹣1)×(﹣2.5)×(﹣).
【解答】(1)原式=.
(2)原式=.
20.计算:
(1)(﹣)×(﹣)×(﹣);
(2)(﹣5)×(﹣)××0×(﹣325).
【解答】解:(1)(﹣)×(﹣)×(﹣)
=﹣××
=﹣;
(2)(﹣5)×(﹣)××0×(﹣325)
=0.
21.已知|a|=5,|b|=7.
(1)若ab<0,求|a﹣b|的值.
(2)若|a﹣b|=﹣(a﹣b),求a b的值.
【解答】解:∵|a|=5,|b|=7,
∴a=±5,b=±7,
(1)若ab<0,所以a,b异号,
当a=5,b=﹣7时,|a﹣b|=|5﹣(﹣7)|=12,
当a=﹣5,b=7时,|a﹣b|=|﹣5﹣7|=12,
综上,|a﹣b|=12;
(2)若|a﹣b|=﹣(a﹣b),则a﹣b≤0,
当a=5,b=7时,a b=5×7=35,
当a=﹣5,b=7时,a b=﹣5×7=﹣35,
综上,ab=±35.
22.设a、b、c为非零有理数|a|+a=0,|ab|=ab,|c|﹣c=0.化简:|b|﹣|a+b|﹣|c﹣b|+|a﹣c|.
【解答】解:∵|a|+a=0,|ab|=ab,|c|﹣c=0,
∴a<0,b<0,c>0,
∴|b|﹣|a+b|﹣|c﹣b|+|a﹣c|
=﹣b﹣(﹣a﹣b)﹣(c﹣b)+c﹣a
=b
一.选择题(共7小题)
1.计算(﹣9)×的结果是( )
A.3 B.27 C.﹣27 D.﹣3
2.若数a的相反数的倒数为1,则数a是( )
A. B. C. D.
3.下列计算正确的个数有( )
①(﹣6)×(﹣5)=﹣30;
②(﹣4)×3=﹣12;
③(﹣6)×0=﹣6;
④×=﹣1.
A.1个 B.2个 C.3个 D.4个
4.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0
B.a<0,b>0
C.a、b同号
D.a、b异号,且正数的绝对值较大
5.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则的值为( )
A. B.99! C.9900 D.2!
6.已知a=(﹣12)×(﹣23)×(﹣34)×(﹣45),b=(﹣123)×(﹣234)×(﹣345),判断下列叙述何者正确?( )
A.a,b皆为正数 B.a,b皆为负数
C.a为正数,b为负数 D.a为负数,b为正数
7.在下面五个说法中正确的有( )
①互为相反数的两个数的绝对值相等
②没有最大的整数,最大的负整数是﹣1,最小的正数是1
③一个数的相反数等于它本身,这个数是0
④任何有理数的绝对值都是正数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题)
8.已知|a|=4,|b|=2,那么ab= .
9.若a<c<0<b,则a×b×c 0.(用“>”“=”“<”填空)
10.已知4个不相等的整数a、b、c、d,它们的积abcd=25,则a+b+c+d= .
11.在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,所得的积最大为a,再取三个数所得的积最小为b,则a+b= .
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为5,则x2+(a+b)2018+(﹣cd)2017的值为 .
13.已知a是不等于﹣1的数,我们把称为a的和倒数.如:2的和倒数为=,已知a1=1,a2是a1的和倒数,a3是a2的和倒数.a4是a3的和倒数,…,依此类推,则a1 a2 a3…a10= .
14.若a、b、c是非零有理数,a+b+c=0,则++﹣的值为 .
三.解答题(共8小题)
15.计算:
(1)(﹣0.12)×(﹣0.25);
(2)×(﹣);
(3)(﹣1)×.
16.计算:
(1)(﹣2)×(﹣8)×(+5)×(﹣);
(2)(﹣0.25)×(﹣)×5×(﹣7);
(3)(﹣3)×(+)×(﹣1)×(﹣)×(+1);
(4)(﹣0.25)×(﹣7)×32×0.125×(﹣)×0.
17.计算:
(1)(﹣0.4)×(+25)×(﹣5);
(2)(﹣10)×(﹣0.1)×(﹣8.25);
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1);
(4)(﹣3)××(﹣)×(﹣);
(5)(﹣8)×[﹣(﹣)];
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2);
(7)(﹣)×(﹣1);
(8)(﹣)×2.5×(﹣)×(﹣8);
(9)(﹣3)××(﹣)×(﹣);
(10)(﹣4)×7×(﹣1)×(﹣0.25).
18.计算:
(1)(﹣3)××(﹣)×(﹣);
(2)3×(﹣0.3)×(﹣1)×(﹣2);
(3)(﹣5)×(﹣6)×3×(﹣2);
(4)(﹣3)×(﹣1)×2×0×(﹣2);
(5)(﹣5.6)×(﹣4.2)×2×(﹣);
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5.
19.计算:
(1)(﹣7)×8×()×;
(2)1.6×(﹣1)×(﹣2.5)×(﹣).
20.计算:
(1)(﹣)×(﹣)×(﹣);
(2)(﹣5)×(﹣)××0×(﹣325).
21.已知|a|=5,|b|=7.
(1)若ab<0,求|a﹣b|的值.
(2)若|a﹣b|=﹣(a﹣b),求a b的值.
22.设a、b、c为非零有理数|a|+a=0,|ab|=ab,|c|﹣c=0.化简:|b|﹣|a+b|﹣|c﹣b|+|a﹣c|.
专题09 : 2021年人教新版七年级(上册)1.4 有理数的乘除法 -期末考复习专题训练
参考答案与试题解析
一.选择题(共7小题)
1.计算(﹣9)×的结果是( )
A.3 B.27 C.﹣27 D.﹣3
【解答】解:原式=﹣(9×)=﹣3,
故选:D.
2.若数a的相反数的倒数为1,则数a是( )
A. B. C. D.
【解答】解:数a的相反数是﹣a,﹣a的倒数是﹣,
所以﹣=1,
所以a=﹣.
故选:C.
3.下列计算正确的个数有( )
①(﹣6)×(﹣5)=﹣30;
②(﹣4)×3=﹣12;
③(﹣6)×0=﹣6;
④×=﹣1.
A.1个 B.2个 C.3个 D.4个
【解答】解:①(﹣6)×(﹣5)=30;故①不合题意;
②(﹣4)×3=﹣12;故②符合题意;
③(﹣6)×0=0;,故③不合题意;
④×(﹣)=﹣1,故④合题意;
∴正确的有两个,
故选:B.
4.已知两个有理数a,b,如果ab<0且a+b>0,那么( )
A.a>0,b>0
B.a<0,b>0
C.a、b同号
D.a、b异号,且正数的绝对值较大
【解答】解:∵ab<0,
∴a,b异号,
∵a+b>0,
∴正数的绝对值较大,
故选:D.
5.若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则的值为( )
A. B.99! C.9900 D.2!
【解答】解:原式=
=99×100
=9900.
故选:C.
6.已知a=(﹣12)×(﹣23)×(﹣34)×(﹣45),b=(﹣123)×(﹣234)×(﹣345),判断下列叙述何者正确?( )
A.a,b皆为正数 B.a,b皆为负数
C.a为正数,b为负数 D.a为负数,b为正数
【解答】解:∵a=(﹣12)×(﹣23)×(﹣34)×(﹣45)中共有4个负数相乘,
∴a为正数,
∵b=(﹣123)×(﹣234)×(﹣345)中共有3个负数相乘,
∴b为负数,
∴a为正数,b为负数,
故选:C.
7.在下面五个说法中正确的有( )
①互为相反数的两个数的绝对值相等
②没有最大的整数,最大的负整数是﹣1,最小的正数是1
③一个数的相反数等于它本身,这个数是0
④任何有理数的绝对值都是正数
⑤几个有理数相乘,如果负因数有奇数个,则积为负数.
A.1个 B.2个 C.3个 D.4个
【解答】解:互为相反数的两个数的绝对值相等,故①正确,
没有最大的整数,最大的负整数是﹣1,最小的正数也没有,故②错误,
一个数的相反数等于它本身,这个数是0,故③正确,
任何有理数的绝对值都是非负数,故④错误,
几个不为零的有理数相乘,如果负因数有奇数个,则积为负数,故⑤错误,
故选:B.
二.填空题(共7小题)
8.已知|a|=4,|b|=2,那么ab= 8或﹣8 .
【解答】解:∵|a|=4,|b|=2,
∴a=±4,b=±2,
∴a=4,b=2时,ab=4×2=8;
当a=4,b=﹣2时,ab=4×(﹣2)=﹣8.
当a=﹣4,b=2时,ab=(﹣4)×2=﹣8.
当a=﹣4,b=﹣2时,ab=(﹣4)×(﹣2)=8.
∴ab的值为8或﹣8.
故答案为:8或﹣8.
9.若a<c<0<b,则a×b×c > 0.(用“>”“=”“<”填空)
【解答】解:∵a<c<0<b,
∴a,c为负数,b为正数,
∴a×c>0,
∴a×b×c>0.
故答案为>.
10.已知4个不相等的整数a、b、c、d,它们的积abcd=25,则a+b+c+d= 0 .
【解答】解:∵a、b、c、d是4个不相等的整数,
∴25=1×5×(﹣1)×(﹣5),
∴a+b+c+d=1+5+(﹣1)+(﹣5)=0;
故答案为0.
11.在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,所得的积最大为a,再取三个数所得的积最小为b,则a+b= ﹣24 .
【解答】解:在﹣2,3,4,﹣6这四个数中,取其中三个数相乘,一共有四种情况:
①(﹣2)×3×4=﹣24,
②(﹣2)×3×(﹣6)=36,
③(﹣2)×4×(﹣6)=48,
④3×4×(﹣6)=﹣72,
∵所得的积最大为a,再取三个数所得的积最小为b,
∴a=48,b=﹣72,
∴a+b=﹣24,
故答案为:﹣24.
12.已知a,b互为相反数,c,d互为倒数,x的绝对值为5,则x2+(a+b)2018+(﹣cd)2017的值为 24 .
【解答】解:根据题中的新定义化简得:a+b=0,cd=1,x=5或﹣5,
则原式=25+0﹣1=24.
故答案为:24.
13.已知a是不等于﹣1的数,我们把称为a的和倒数.如:2的和倒数为=,已知a1=1,a2是a1的和倒数,a3是a2的和倒数.a4是a3的和倒数,…,依此类推,则a1 a2 a3…a10= .
【解答】解:a1=1,a2=,a3==,,,,,,,,
则a1 a2 a3…a10=1×=.
故答案为:.
14.若a、b、c是非零有理数,a+b+c=0,则++﹣的值为 ﹣3或3 .
【解答】解:∵a、b、c是非零有理数,a+b+c=0,
∴当a、b、c中一正两负时,
不妨设a>0,b<0,c<0,则a=﹣(b+c),
故++﹣=1+(﹣1)+(﹣1)﹣2=﹣3;
当a、b、c中两正一负时,
不妨设a>0,b>0,c<0,则c=﹣(a+b),
故++﹣=1+1+(﹣1)+2=3;
故答案为:﹣3或3.
三.解答题(共8小题)
15.计算:
(1)(﹣0.12)×(﹣0.25);
(2)×(﹣);
(3)(﹣1)×.
【解答】解:(1)(﹣0.12)×(﹣0.25)
=
=0.03;
(2)
=
=;
(3)
=
=﹣1.
16.计算:
(1)(﹣2)×(﹣8)×(+5)×(﹣);
(2)(﹣0.25)×(﹣)×5×(﹣7);
(3)(﹣3)×(+)×(﹣1)×(﹣)×(+1);
(4)(﹣0.25)×(﹣7)×32×0.125×(﹣)×0.
【解答】解:(1)(﹣2)×(﹣8)×(+5)×(﹣),
=16×(﹣)
=;
(2)(﹣0.25)×()×5×(﹣7),
=(﹣0.25)×5×[(﹣)×(﹣7)],
=﹣×4,
=﹣5;
(3),
=,
=;
(4)
=0.
17.计算:
(1)(﹣0.4)×(+25)×(﹣5);
(2)(﹣10)×(﹣0.1)×(﹣8.25);
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1);
(4)(﹣3)××(﹣)×(﹣);
(5)(﹣8)×[﹣(﹣)];
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2);
(7)(﹣)×(﹣1);
(8)(﹣)×2.5×(﹣)×(﹣8);
(9)(﹣3)××(﹣)×(﹣);
(10)(﹣4)×7×(﹣1)×(﹣0.25).
【解答】解:(1)(﹣0.4)×(+25)×(﹣5)
=+(0.4×25×5)
=50;
(2)(﹣10)×(﹣0.1)×(﹣8.25)
=﹣(10×0.1×8.25)
=﹣8.25;
(3)(﹣1)×(﹣)×××(﹣)×0×(﹣1)
=0;
(4)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(5)(﹣8)×[﹣(﹣)]
=(﹣8)×
=﹣2;
(6)(﹣2.5)×(+4)×(﹣0.3)×(+33)×(﹣2)
=﹣(2.5×4)×(0.3×)×2
=﹣10×10×2
=﹣200;
(7)(﹣)×(﹣1)
=×
=;
(8)(﹣)×2.5×(﹣)×(﹣8)
=﹣(×2.5)×(×8)
=﹣×
=﹣;
(9)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(10)(﹣4)×7×(﹣1)×(﹣0.25)
=﹣(4×0.25×7×1)
=﹣7.
18.计算:
(1)(﹣3)××(﹣)×(﹣);
(2)3×(﹣0.3)×(﹣1)×(﹣2);
(3)(﹣5)×(﹣6)×3×(﹣2);
(4)(﹣3)×(﹣1)×2×0×(﹣2);
(5)(﹣5.6)×(﹣4.2)×2×(﹣);
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5.
【解答】解:(1)(﹣3)××(﹣)×(﹣)
=﹣(3×××)
=﹣;
(2)3×(﹣0.3)×(﹣1)×(﹣2)
=﹣×××
=﹣;
(3)(﹣5)×(﹣6)×3×(﹣2)
=﹣5×6×3×2
=﹣180;
(4)(﹣3)×(﹣1)×2×0×(﹣2)
=0;
(5)(﹣5.6)×(﹣4.2)×2×(﹣)
=﹣(5.6×4.2××)
=﹣18;
(6)(﹣)×(﹣3)×(﹣4)×(﹣1)×(﹣25)×5
=﹣××(4×25)×3×5
=﹣1×100×15
=﹣1500.
19.计算:
(1)(﹣7)×8×()×;
(2)1.6×(﹣1)×(﹣2.5)×(﹣).
【解答】(1)原式=.
(2)原式=.
20.计算:
(1)(﹣)×(﹣)×(﹣);
(2)(﹣5)×(﹣)××0×(﹣325).
【解答】解:(1)(﹣)×(﹣)×(﹣)
=﹣××
=﹣;
(2)(﹣5)×(﹣)××0×(﹣325)
=0.
21.已知|a|=5,|b|=7.
(1)若ab<0,求|a﹣b|的值.
(2)若|a﹣b|=﹣(a﹣b),求a b的值.
【解答】解:∵|a|=5,|b|=7,
∴a=±5,b=±7,
(1)若ab<0,所以a,b异号,
当a=5,b=﹣7时,|a﹣b|=|5﹣(﹣7)|=12,
当a=﹣5,b=7时,|a﹣b|=|﹣5﹣7|=12,
综上,|a﹣b|=12;
(2)若|a﹣b|=﹣(a﹣b),则a﹣b≤0,
当a=5,b=7时,a b=5×7=35,
当a=﹣5,b=7时,a b=﹣5×7=﹣35,
综上,ab=±35.
22.设a、b、c为非零有理数|a|+a=0,|ab|=ab,|c|﹣c=0.化简:|b|﹣|a+b|﹣|c﹣b|+|a﹣c|.
【解答】解:∵|a|+a=0,|ab|=ab,|c|﹣c=0,
∴a<0,b<0,c>0,
∴|b|﹣|a+b|﹣|c﹣b|+|a﹣c|
=﹣b﹣(﹣a﹣b)﹣(c﹣b)+c﹣a
=b
