24.2.2 第1课时 直线和圆的位置关系 课时作业(含答案)
文档属性
| 名称 | 24.2.2 第1课时 直线和圆的位置关系 课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 269.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 17:22:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十四章 圆
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
1. 已知☉O的半径是3,圆心O到直线l的距离是4,则直线l与☉O的公共点的个数是( )
A.0 B.1 C.2 D.1或2
2. 著名作家巴金在他的作品《海上日出》中对日出有这样一段描写:“果然,过了一会儿,那里出现了太阳的小半边脸,红是红得很,却没有亮光.”这段文字中,给我们呈现了直线与圆的哪一种位置关系( )
A.相离 B.相切 C.相交 D.无法确定
3. 已知某正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了( )
A.6圈 B.6.5圈 C.7圈 D.8圈
4. 已知半径为3的☉O上一点P和☉O外一点Q,如果OQ=5,PQ=4,则PQ与☉O的位置关系是( )
A.相交 B.相切 C.相离 D.位置不定
5. 已知☉O的半径是一元二次方程x2-3x-4=0的一个根,圆心O到直线l的距离d=6,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
6. 已知☉M在平面直角坐标系中,点M的坐标是(2,4),☉M的半径为r,当☉M与坐标轴恰好有三个交点时,r应满足( )
A.r=4或2 B.r=4 C.r= D.4≤r≤2
7. 在△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心,以R长为半径画圆,若☉C与边AB只有一个公共点,则R的取值范围是( )
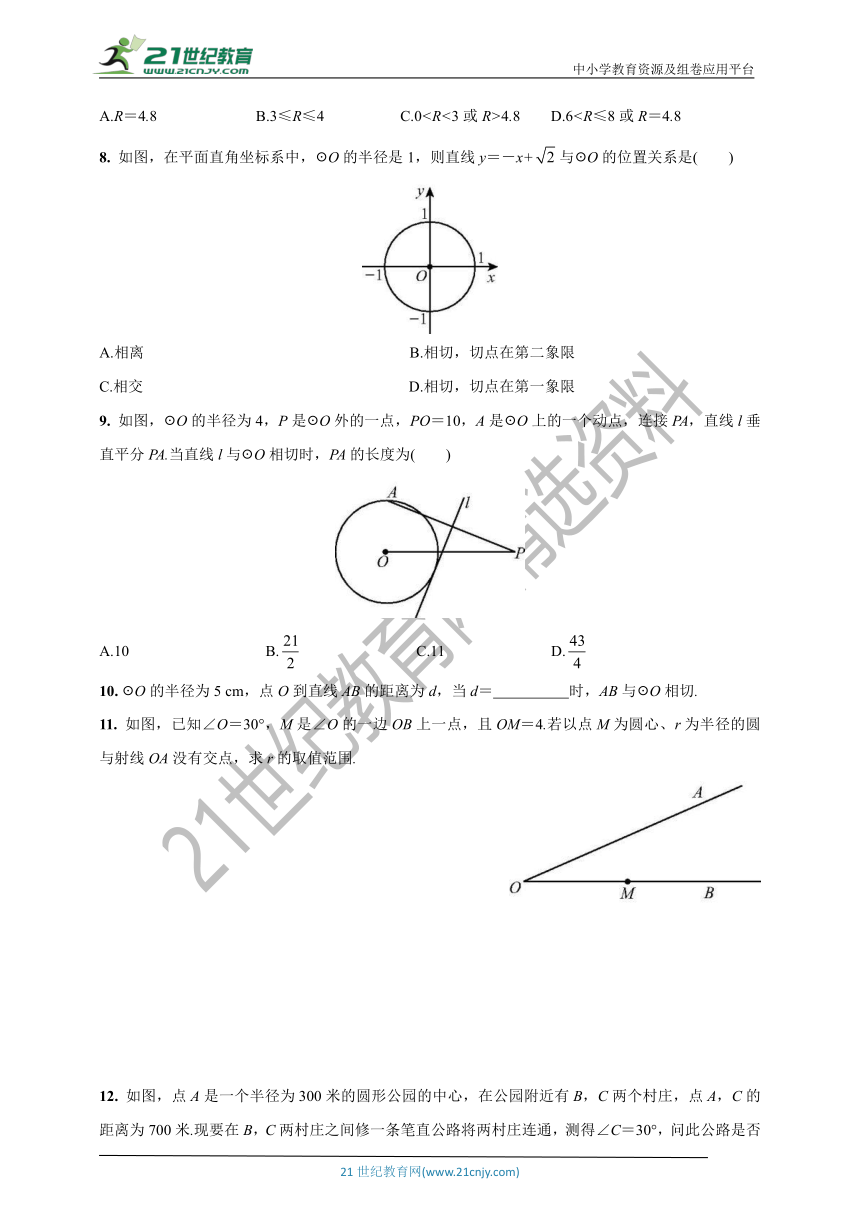
A.R=4.8 B.3≤R≤4 C.04.8 D.68. 如图,在平面直角坐标系中,☉O的半径是1,则直线y=-x+与☉O的位置关系是( )
A.相离 B.相切,切点在第二象限
C.相交 D.相切,切点在第一象限
9. 如图,☉O的半径为4,P是☉O外的一点,PO=10,A是☉O上的一个动点,连接PA,直线l垂直平分PA.当直线l与☉O相切时,PA的长度为( )
A.10 B. C.11 D.
10. ☉O的半径为5 cm,点O到直线AB的距离为d,当d= 时,AB与☉O相切.
11. 如图,已知∠O=30°,M是∠O的一边OB上一点,且OM=4.若以点M为圆心、r为半径的圆与射线OA没有交点,求r的取值范围.
12. 如图,点A是一个半径为300米的圆形公园的中心,在公园附近有B,C两个村庄,点A,C的距离为700米.现要在B,C两村庄之间修一条笔直公路将两村庄连通,测得∠C=30°,问此公路是否穿过该公园 请通过计算进行说明.
13. 如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以点P为圆心、50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/小时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
14. 如图,△ABC是边长为4 cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1 cm/s,点Q沿CA,AB向终点B运动,速度为2 cm/s.若P,Q两点同时出发,设它们的运动时间为x s.
(1)求x为何值时,PQ⊥AC x为何值时,PQ⊥AB
(2)当0(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系时的x的取值范围(不要求写出过程).
参 考 答 案
1. A 2. C 3. A 4. B 5. A 6. A 7. D 8. D 9. B
10. 5 cm
11. 解:r的取值范围是012. 解:此公路不会穿过该公园. 理由:作AM⊥BC于点M,由已知条件易得AM=350>300,所以此公路不会穿过该公园.
13. 解:(1)过点A作AP⊥ON于点P. 在Rt△AOP中,∠APO=90°,∠POA=30°,OA=80米,所以AP=80×=40(米),即对学校A的噪声影响最大时卡车P与学校A的距离是40米.
(2)以点A为圆心、50米长为半径画弧,交ON于点D,E,在Rt△ADP中,∠APD=90°,AP=40米,AD=50米,所以DP===30(米),所以DE=60米. 又18千米/小时=300米/分,所以=0.2(分)=12(秒),即卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒.
14. 解:(1)当x=(Q在AC上)时,PQ⊥AC. 当x=(Q在AB上)时,PQ⊥AB.
(2)过点Q作QN⊥BC于点N. 当0(3)显然,不存在x的值,使得以PQ为直径的圆与AC相离,当x=或时,以PQ为直径的圆与AC相切,当0≤x<或21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十四章 圆
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
1. 已知☉O的半径是3,圆心O到直线l的距离是4,则直线l与☉O的公共点的个数是( )
A.0 B.1 C.2 D.1或2
2. 著名作家巴金在他的作品《海上日出》中对日出有这样一段描写:“果然,过了一会儿,那里出现了太阳的小半边脸,红是红得很,却没有亮光.”这段文字中,给我们呈现了直线与圆的哪一种位置关系( )
A.相离 B.相切 C.相交 D.无法确定
3. 已知某正三角形的边长是和它相切的圆的周长的两倍,当这个圆按箭头方向从某一位置沿正三角形的三边做无滑动的旋转,直至回到原出发位置时,则这个圆共转了( )
A.6圈 B.6.5圈 C.7圈 D.8圈
4. 已知半径为3的☉O上一点P和☉O外一点Q,如果OQ=5,PQ=4,则PQ与☉O的位置关系是( )
A.相交 B.相切 C.相离 D.位置不定
5. 已知☉O的半径是一元二次方程x2-3x-4=0的一个根,圆心O到直线l的距离d=6,则直线l与☉O的位置关系是( )
A.相离 B.相切 C.相交 D.无法判断
6. 已知☉M在平面直角坐标系中,点M的坐标是(2,4),☉M的半径为r,当☉M与坐标轴恰好有三个交点时,r应满足( )
A.r=4或2 B.r=4 C.r= D.4≤r≤2
7. 在△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心,以R长为半径画圆,若☉C与边AB只有一个公共点,则R的取值范围是( )
A.R=4.8 B.3≤R≤4 C.0
A.相离 B.相切,切点在第二象限
C.相交 D.相切,切点在第一象限
9. 如图,☉O的半径为4,P是☉O外的一点,PO=10,A是☉O上的一个动点,连接PA,直线l垂直平分PA.当直线l与☉O相切时,PA的长度为( )
A.10 B. C.11 D.
10. ☉O的半径为5 cm,点O到直线AB的距离为d,当d= 时,AB与☉O相切.
11. 如图,已知∠O=30°,M是∠O的一边OB上一点,且OM=4.若以点M为圆心、r为半径的圆与射线OA没有交点,求r的取值范围.
12. 如图,点A是一个半径为300米的圆形公园的中心,在公园附近有B,C两个村庄,点A,C的距离为700米.现要在B,C两村庄之间修一条笔直公路将两村庄连通,测得∠C=30°,问此公路是否穿过该公园 请通过计算进行说明.
13. 如图,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿道路ON方向行驶时,在以点P为圆心、50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/小时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
14. 如图,△ABC是边长为4 cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1 cm/s,点Q沿CA,AB向终点B运动,速度为2 cm/s.若P,Q两点同时出发,设它们的运动时间为x s.
(1)求x为何值时,PQ⊥AC x为何值时,PQ⊥AB
(2)当0
参 考 答 案
1. A 2. C 3. A 4. B 5. A 6. A 7. D 8. D 9. B
10. 5 cm
11. 解:r的取值范围是0
13. 解:(1)过点A作AP⊥ON于点P. 在Rt△AOP中,∠APO=90°,∠POA=30°,OA=80米,所以AP=80×=40(米),即对学校A的噪声影响最大时卡车P与学校A的距离是40米.
(2)以点A为圆心、50米长为半径画弧,交ON于点D,E,在Rt△ADP中,∠APD=90°,AP=40米,AD=50米,所以DP===30(米),所以DE=60米. 又18千米/小时=300米/分,所以=0.2(分)=12(秒),即卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒.
14. 解:(1)当x=(Q在AC上)时,PQ⊥AC. 当x=(Q在AB上)时,PQ⊥AB.
(2)过点Q作QN⊥BC于点N. 当0
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
