2021-2022学年人教版数学九年级上册第13讲二次函数y=ax2+ bx+c(a≠0)的图象与性质期末复习讲义
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册第13讲二次函数y=ax2+ bx+c(a≠0)的图象与性质期末复习讲义 |  | |
| 格式 | zip | ||
| 文件大小 | 207.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 16:46:34 | ||
图片预览



文档简介
第13讲 二次函数y=ax +bx+c(a≠0)的图象与性质
【要点梳理】
要点一、二次函数与之间的相互关系
1.顶点式化成一般式
从函数解析式我们可以直接得到抛物线的顶点(h,k),所以我们称为顶点式,将顶点式去括号,合并同类项就可化成一般式.
2.一般式化成顶点式
.
对照,可知,.
∴ 抛物线的对称轴是直线,顶点坐标是.
要点诠释:
1.抛物线的对称轴是直线,顶点坐标是,可以当作公式加以记忆和运用.
2.求抛物线的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.
要点二、二次函数的图象的画法
1.一般方法:列表、描点、连线;
2.简易画法:五点定形法.
其步骤为:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线与坐标轴的交点,
当抛物线与x轴有两个交点时,描出这两个交点A、B及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A、B、C、D及M这五个点按从左到右的顺序用平滑曲线连结起来.
要点诠释:
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及对称点D,由C、M、D三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A、B,然后顺次用平滑曲线连结五点,画出二次函数的图象,
要点三、二次函数的图象与性质
1.二次函数图象与性质
函数 二次函数(a、b、c为常数,a≠0)
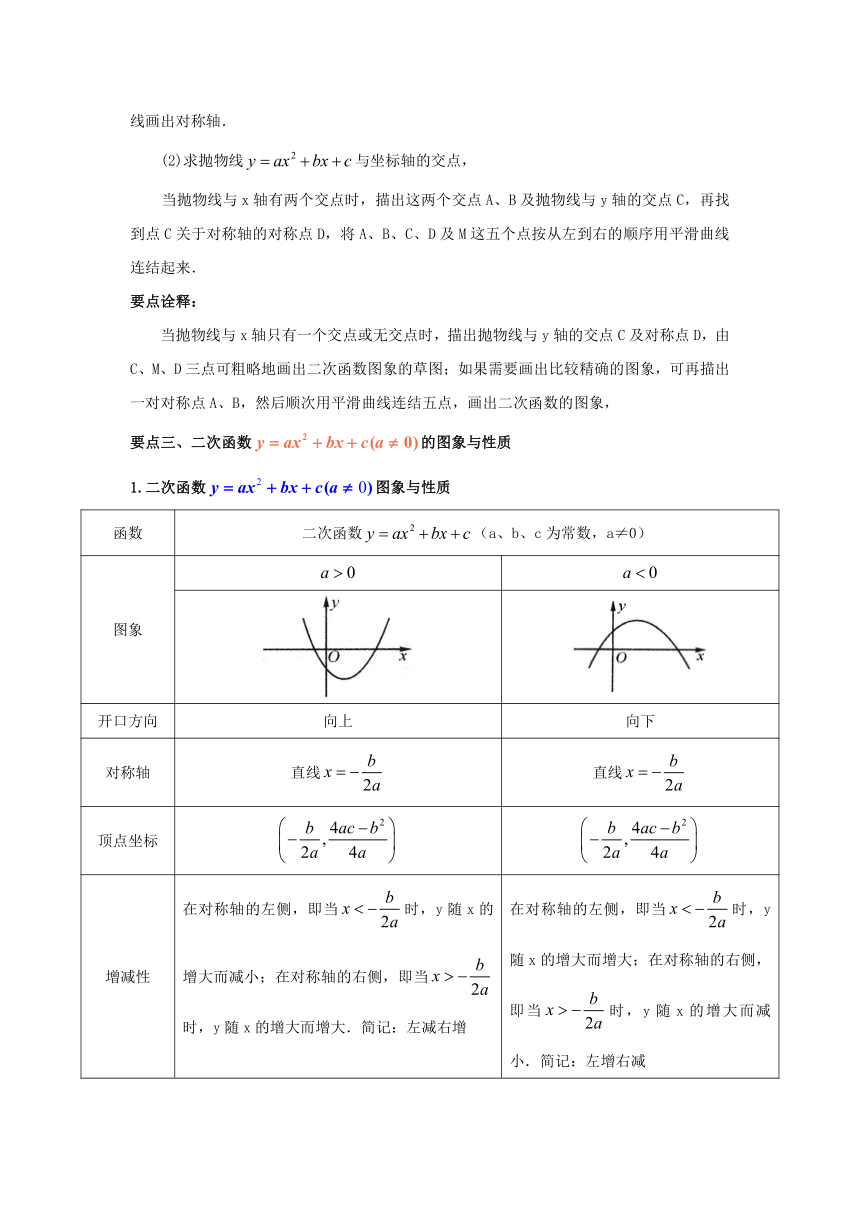
图象
开口方向 向上 向下
对称轴 直线 直线
顶点坐标
增减性 在对称轴的左侧,即当时,y随x的增大而减小;在对称轴的右侧,即当时,y随x的增大而增大.简记:左减右增 在对称轴的左侧,即当时,y随x的增大而增大;在对称轴的右侧,即当时,y随x的增大而减小.简记:左增右减
最大(小)值 抛物线有最低点,当时,y有最小值, 抛物线有最高点,当时,y有最大值,
2.二次函数图象的特征与a、b、c及b2-4ac的符号之间的关系
项目 字母 字母的符号 图象的特征
a a>0 开口向上
a<0 开口向下
b ab>0(a,b同号) 对称轴在y轴左侧
ab<0(a,b异号) 对称轴在y轴右侧
c c=0 图象过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
要点四、求二次函数的最大(小)值的方法
如果自变量的取值范围是全体实数,那么函数在顶点处取得最大(或最小)值,即当时,.
要点诠释:
如果自变量的取值范围是x1≤x≤x2,那么首先要看是否在自变量的取值范围x1≤x≤x2内,若在此范围内,则当时,,若不在此范围内,则需要考虑函数在x1≤x≤x2范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2时,;当x=x1时,,如果在此范围内,y随x的增大而减小,则当x=x1时,;当x=x2时,,如果在此范围内,y值有增有减,则需考察x=x1,x=x2,时y值的情况.
【典型例题】
类型一、二次函数的图象与性质
1.求抛物线的对称轴和顶点坐标.
举一反三:
【变式】把一般式化为顶点式.
(1)写出其开口方向、对称轴和顶点D的坐标;
(2)分别求出它与y轴的交点C,与x轴的交点A、B的坐标.
2. 二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A. B.C.D.
类型二、二次函数的最值
求二次函数的最小值
对应练习
1.二次函数y=﹣3x2+6x变形为y=a(x+m)2+n形式,正确的是( )
A. y=﹣3(x+1)2﹣3 B. y=﹣3(x﹣1)2﹣3
C. y=﹣3(x+1)2+3 D. y=﹣3(x﹣1)2+3
2.抛物线y=x2﹣2x﹣3的对称轴是( )
A. x=1 B. x=﹣1 C. x=2 D. x=﹣2
3.抛物线y=x2+2x-3的最小值是( )
A. 3 B. -3 C. 4 D. -4
4.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1 , y2 , y3的大小关系是( )
A. y3>y2>y1 B. y3>y1=y2 C. y1>y2>y3 D. y1=y2>y3
5.在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A. B. C. D.
6.函数y=﹣x2﹣4x﹣3图象顶点坐标是( )
A. (2,﹣1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,1)
7点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1 y2.
8.若点(1,5),(5,5)是抛物线y=ax2+bx+c上的两个点,则此抛物线的对称轴是 .
8.如果二次函数y=x2﹣8x+m﹣1的顶点在x轴上,那么m= .
9.若二次函数 的图象与x轴的一个交点是(2,0),则与x轴的另一个交点坐标是 .
10.已知二次函数y=x2﹣4x+5.
(1)将y=x2﹣4x+5化成y=a(x﹣h)2+k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
已知二次函数y=x2﹣4x+3.
①求出这个二次函数图象的对称轴和顶点坐标;
②求出这个二次函数的图象与坐标轴的交点;
③直接写出y>0时x的范围
已知二次函数y=-2x2+8x-6,完成下列各题:
(1)将函数关系式用配方法化为y=a(x+h)2+k的形式,并写出它的顶点坐标、对称轴;
(2)它的图象与x轴交于A,B两点,顶点为C,求S△ABC.
13.已知:二次函数y=x2﹣4x+3.
(1)将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y<0.
14.已知抛物线y=﹣x2+4x+5.
(1)用配方法将y=﹣x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
二次函数y=ax^2+bx+c的图象和性质
精选练习
一、单选题(共10小题)
1.(2020·蚌埠市期末)关于二次函数,下列说法正确的是( )
A.图像与轴的交点坐标为 B.图像的对称轴在轴的右侧
C.当时,的值随值的增大而减小 D.的最小值为-3
2.(2020·黄冈市期中)抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
A.先向左平移2个单位长度,然后向上平移1个单位长度
B.先向左平移2个单位长度,然后向下平移1个单位长度
C.先向右平移2个单位长度,然后向上平移1个单位长度
D.先向右平移2个单位长度,然后向下平移1个单位长度
3.(2020·福州市期中)已知抛物线经过和两点,则n的值为( )
A.﹣2 B.﹣4 C.2 D.4
4.(2020·浏阳市期中)将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
5.(2020·沈阳市期末)抛物线y=x2﹣2x+2的顶点坐标为( )
A.(1,1) B.(﹣1,1) C.(1,3) D.(﹣1,3)
6.在同一坐标系中,一次函数与二次函数的图象可能是( ).
A. B. C.D.
7.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
8.(2020·青岛市期中)如图,二次函数的图象开口向下,且经过第三象限的点若点P的横坐标为,则一次函数的图象大致是
A. B.C. D.
9.(2018·烟台市期末)如图,函数和(是常数,且)在同一平面直角坐标系的图象可能是( )
A. B. C.D.
10.(2019·枣庄市期中)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
二、填空题(共5小题)
11.(2020·鸡西市期末)已知A(0,3),B(2,3)是抛物线上两点,该抛物线的顶点坐标是_________.
12.(2019·宁波市期末)已知抛物线的对称轴是直线,其部分图象如图所示,下列说法中:①;②;③;④当时,,正确的是_____(填写序号).
13.(2018·许昌市期末)抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是_____.
14.(2018·宿迁市期末)若抛物线C1:y=x2+mx+2与抛物线C2:y=x2﹣3x+n关于y轴对称,则m+n=_____.
15.(2018·襄阳市期末)将抛物线向右平移3个单位,再向上平移3个单位,所得的抛物线的解析式为________________.
三、解答题(共2小题)
16.(2020·长春市期末)已知抛物线经过点A(3,0),B(﹣1,0).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
17.(2019·合肥市期中)已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
【要点梳理】
要点一、二次函数与之间的相互关系
1.顶点式化成一般式
从函数解析式我们可以直接得到抛物线的顶点(h,k),所以我们称为顶点式,将顶点式去括号,合并同类项就可化成一般式.
2.一般式化成顶点式
.
对照,可知,.
∴ 抛物线的对称轴是直线,顶点坐标是.
要点诠释:
1.抛物线的对称轴是直线,顶点坐标是,可以当作公式加以记忆和运用.
2.求抛物线的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用.
要点二、二次函数的图象的画法
1.一般方法:列表、描点、连线;
2.简易画法:五点定形法.
其步骤为:
(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M,并用虚线画出对称轴.
(2)求抛物线与坐标轴的交点,
当抛物线与x轴有两个交点时,描出这两个交点A、B及抛物线与y轴的交点C,再找到点C关于对称轴的对称点D,将A、B、C、D及M这五个点按从左到右的顺序用平滑曲线连结起来.
要点诠释:
当抛物线与x轴只有一个交点或无交点时,描出抛物线与y轴的交点C及对称点D,由C、M、D三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A、B,然后顺次用平滑曲线连结五点,画出二次函数的图象,
要点三、二次函数的图象与性质
1.二次函数图象与性质
函数 二次函数(a、b、c为常数,a≠0)
图象
开口方向 向上 向下
对称轴 直线 直线
顶点坐标
增减性 在对称轴的左侧,即当时,y随x的增大而减小;在对称轴的右侧,即当时,y随x的增大而增大.简记:左减右增 在对称轴的左侧,即当时,y随x的增大而增大;在对称轴的右侧,即当时,y随x的增大而减小.简记:左增右减
最大(小)值 抛物线有最低点,当时,y有最小值, 抛物线有最高点,当时,y有最大值,
2.二次函数图象的特征与a、b、c及b2-4ac的符号之间的关系
项目 字母 字母的符号 图象的特征
a a>0 开口向上
a<0 开口向下
b ab>0(a,b同号) 对称轴在y轴左侧
ab<0(a,b异号) 对称轴在y轴右侧
c c=0 图象过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
要点四、求二次函数的最大(小)值的方法
如果自变量的取值范围是全体实数,那么函数在顶点处取得最大(或最小)值,即当时,.
要点诠释:
如果自变量的取值范围是x1≤x≤x2,那么首先要看是否在自变量的取值范围x1≤x≤x2内,若在此范围内,则当时,,若不在此范围内,则需要考虑函数在x1≤x≤x2范围内的增减性,如果在此范围内,y随x的增大而增大,则当x=x2时,;当x=x1时,,如果在此范围内,y随x的增大而减小,则当x=x1时,;当x=x2时,,如果在此范围内,y值有增有减,则需考察x=x1,x=x2,时y值的情况.
【典型例题】
类型一、二次函数的图象与性质
1.求抛物线的对称轴和顶点坐标.
举一反三:
【变式】把一般式化为顶点式.
(1)写出其开口方向、对称轴和顶点D的坐标;
(2)分别求出它与y轴的交点C,与x轴的交点A、B的坐标.
2. 二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=ax+b的图象大致是( )
A. B.C.D.
类型二、二次函数的最值
求二次函数的最小值
对应练习
1.二次函数y=﹣3x2+6x变形为y=a(x+m)2+n形式,正确的是( )
A. y=﹣3(x+1)2﹣3 B. y=﹣3(x﹣1)2﹣3
C. y=﹣3(x+1)2+3 D. y=﹣3(x﹣1)2+3
2.抛物线y=x2﹣2x﹣3的对称轴是( )
A. x=1 B. x=﹣1 C. x=2 D. x=﹣2
3.抛物线y=x2+2x-3的最小值是( )
A. 3 B. -3 C. 4 D. -4
4.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1 , y2 , y3的大小关系是( )
A. y3>y2>y1 B. y3>y1=y2 C. y1>y2>y3 D. y1=y2>y3
5.在同一平面直角坐标系中,函数y=ax2﹣bx与y=bx+a的图象可能是( )
A. B. C. D.
6.函数y=﹣x2﹣4x﹣3图象顶点坐标是( )
A. (2,﹣1) B. (﹣2,1) C. (﹣2,﹣1) D. (2,1)
7点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1 y2.
8.若点(1,5),(5,5)是抛物线y=ax2+bx+c上的两个点,则此抛物线的对称轴是 .
8.如果二次函数y=x2﹣8x+m﹣1的顶点在x轴上,那么m= .
9.若二次函数 的图象与x轴的一个交点是(2,0),则与x轴的另一个交点坐标是 .
10.已知二次函数y=x2﹣4x+5.
(1)将y=x2﹣4x+5化成y=a(x﹣h)2+k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
已知二次函数y=x2﹣4x+3.
①求出这个二次函数图象的对称轴和顶点坐标;
②求出这个二次函数的图象与坐标轴的交点;
③直接写出y>0时x的范围
已知二次函数y=-2x2+8x-6,完成下列各题:
(1)将函数关系式用配方法化为y=a(x+h)2+k的形式,并写出它的顶点坐标、对称轴;
(2)它的图象与x轴交于A,B两点,顶点为C,求S△ABC.
13.已知:二次函数y=x2﹣4x+3.
(1)将y=x2﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y<0.
14.已知抛物线y=﹣x2+4x+5.
(1)用配方法将y=﹣x2+4x+5化成y=a(x﹣h)2+k的形式;
(2)指出抛物线的开口方向、对称轴和顶点坐标;
(3)若抛物线上有两点A(x1,y1),B(x2,y2),如果x1>x2>2,试比较y1与y2的大小.
二次函数y=ax^2+bx+c的图象和性质
精选练习
一、单选题(共10小题)
1.(2020·蚌埠市期末)关于二次函数,下列说法正确的是( )
A.图像与轴的交点坐标为 B.图像的对称轴在轴的右侧
C.当时,的值随值的增大而减小 D.的最小值为-3
2.(2020·黄冈市期中)抛物线y=(x﹣2)2﹣1可以由抛物线y=x2平移而得到,下列平移正确的是( )
A.先向左平移2个单位长度,然后向上平移1个单位长度
B.先向左平移2个单位长度,然后向下平移1个单位长度
C.先向右平移2个单位长度,然后向上平移1个单位长度
D.先向右平移2个单位长度,然后向下平移1个单位长度
3.(2020·福州市期中)已知抛物线经过和两点,则n的值为( )
A.﹣2 B.﹣4 C.2 D.4
4.(2020·浏阳市期中)将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
5.(2020·沈阳市期末)抛物线y=x2﹣2x+2的顶点坐标为( )
A.(1,1) B.(﹣1,1) C.(1,3) D.(﹣1,3)
6.在同一坐标系中,一次函数与二次函数的图象可能是( ).
A. B. C.D.
7.已知点在抛物线上,则下列结论正确的是( )
A. B. C. D.
8.(2020·青岛市期中)如图,二次函数的图象开口向下,且经过第三象限的点若点P的横坐标为,则一次函数的图象大致是
A. B.C. D.
9.(2018·烟台市期末)如图,函数和(是常数,且)在同一平面直角坐标系的图象可能是( )
A. B. C.D.
10.(2019·枣庄市期中)如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A.①②④ B.①②⑤ C.②③④ D.③④⑤
二、填空题(共5小题)
11.(2020·鸡西市期末)已知A(0,3),B(2,3)是抛物线上两点,该抛物线的顶点坐标是_________.
12.(2019·宁波市期末)已知抛物线的对称轴是直线,其部分图象如图所示,下列说法中:①;②;③;④当时,,正确的是_____(填写序号).
13.(2018·许昌市期末)抛物线y=﹣x2+bx+c的部分图象如图所示,若y>0,则x的取值范围是_____.
14.(2018·宿迁市期末)若抛物线C1:y=x2+mx+2与抛物线C2:y=x2﹣3x+n关于y轴对称,则m+n=_____.
15.(2018·襄阳市期末)将抛物线向右平移3个单位,再向上平移3个单位,所得的抛物线的解析式为________________.
三、解答题(共2小题)
16.(2020·长春市期末)已知抛物线经过点A(3,0),B(﹣1,0).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
17.(2019·合肥市期中)已知抛物线y=ax2+bx﹣3(a≠0)经过点(﹣1,0),(3,0),求a,b的值.
同课章节目录
