2021-2022学年人教版数学九年级上册第12讲 二次函数y=a(x-h)2+k(a≠0)的图象与性质期末复习讲义
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册第12讲 二次函数y=a(x-h)2+k(a≠0)的图象与性质期末复习讲义 |

|
|
| 格式 | zip | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览


文档简介
第12讲 二次函数y=a(x-h) +k(a≠0)的图象与性质
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号 开口方向 顶点坐标 对称轴 性质
向上 x=h 时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下 x=h 时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号 开口方向 顶点坐标 对称轴 性质
向上 x=h 时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下 x=h 时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
【典型例题】
类型一、二次函数图象及性质
1. 二次函数y=﹣(x﹣3)2+2的顶点的坐标是 ,对称轴是 .
举一反三:
【变式】(2014 荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
把抛物线向上平移2个单位,再向左平移4个单位,得到抛物线,求b,c的值.
【变式】二次函数的图象可以看作是二次函数的图象向 平移4个单位,再向 平移3个单位得到的.
类型二、二次函数性质的综合应用
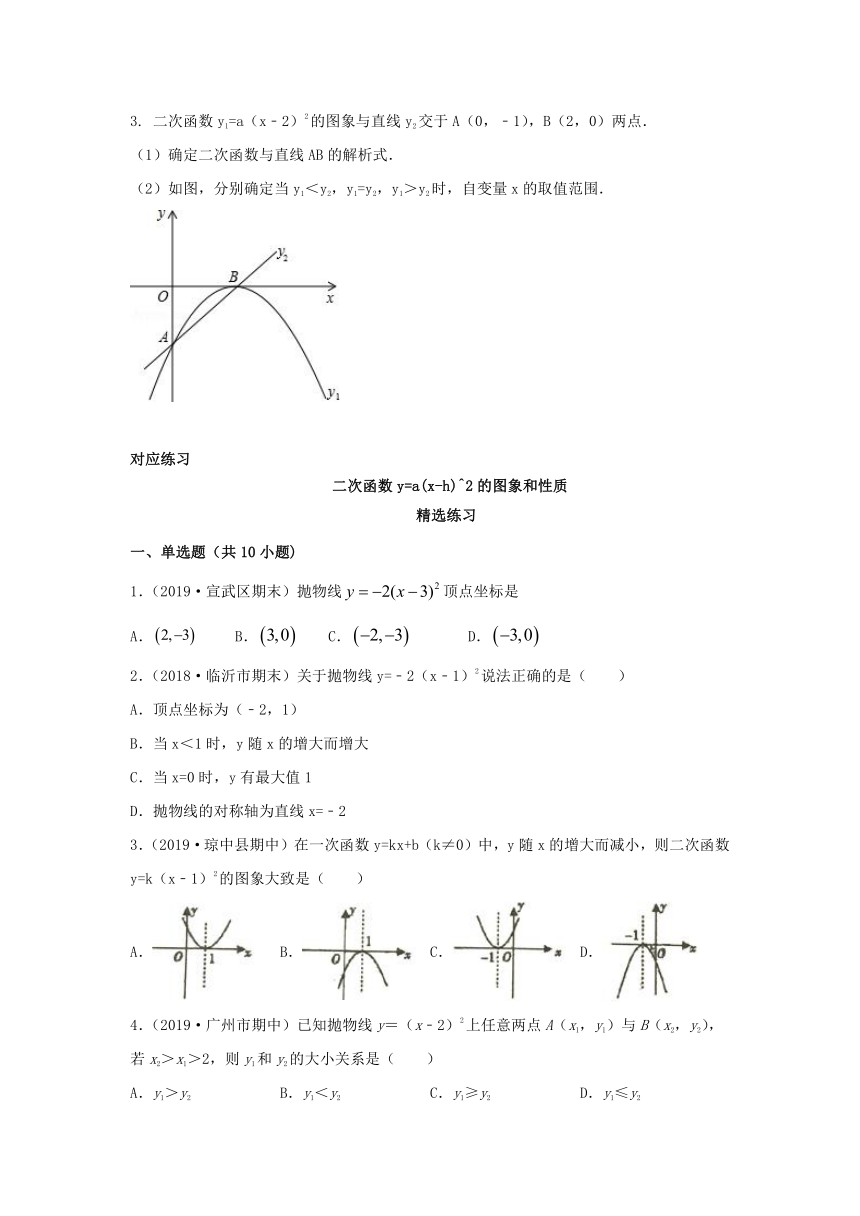
3. 二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
对应练习
二次函数y=a(x-h)^2的图象和性质
精选练习
一、单选题(共10小题)
1.(2019·宣武区期末)抛物线顶点坐标是
A. B. C. D.
2.(2018·临沂市期末)关于抛物线y=﹣2(x﹣1)2说法正确的是( )
A.顶点坐标为(﹣2,1)
B.当x<1时,y随x的增大而增大
C.当x=0时,y有最大值1
D.抛物线的对称轴为直线x=﹣2
3.(2019·琼中县期中)在一次函数y=kx+b(k≠0)中,y随x的增大而减小,则二次函数y=k(x﹣1)2的图象大致是( )
A. B. C. D.
4.(2019·广州市期中)已知抛物线y=(x﹣2)2上任意两点A(x1,y1)与B(x2,y2),若x2>x1>2,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1≥y2 D.y1≤y2
5.(2019·扬州市期末)函数的图象可以由函数的图象( )得到
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
6.抛物线y= (x 5)2不经过的象限是( )
A.第一、二象限 B.第一、四象限 C.第二、三象限 D.第三、四象限
7.关于抛物线①y=x2;②y=–x2+1;③y=(x–2)2,下列结论正确的是( )
A.顶点相同 B.对称轴相同
C.形状相同 D.都有最高点
8.对于抛物线,下列说法正确的是( )
A.最低点坐标(-3, 0) B.最高点坐标(-3, 0) C.最低点坐标(3, 0) D.最高点坐标(3, 0)
9.顶点为(-5,0),且开口方向、形状与函数的图象相同的抛物线是( )
A. B. C. D.
10.已知函数y=(x﹣1)2,下列结论正确的是( )
A.当x>0时,y随x的增大而减小 B.当x<0时,y随x的增大而增大
C.当x<1时,y随x的增大而减小 D.当x<﹣1时,y随x的增大而增大
二、填空题(共5小题)
11.(2018·洛阳市期末)已知函数y=﹣(x﹣1)2图象上两点A(2,y1),B(a,y2),其中a>2,则y1与y2的大小关系是y1_____y2(填“<”、“>”或“=”)
12.(2019·肇庆市期中)二次函数y=3x2+1和y=3(x﹣1)2,以下说法:
①它们的图象开口方向、大小相同;
②它们的对称轴都是y轴,顶点坐标都是原点(0,1);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们与坐标轴都有一个交点;
其中正确的说法有_____.
13.(2018·厦门市期末)抛物线经过点(-2,1),则______。
14.(2018·鼓楼区期末)已知A(-4,y1),B(-3,y2),C(3,y3)三点都在二次函数y=-2(x+2)2的图象上,则y1,y2,y3的大小关系为___.
15.(2019·中山市期中)点A(﹣1,﹣2)在抛物线y=﹣(x﹣1)2上,点A、B关于该抛物线的对称轴对称,则B点坐标为_____.
三、解答题(共2小题)
16.(2018·揭阳市期末)已知二次函数,当时有最大值,且此函数的图象经过点,求此二次函数的关系式,并指出当为何值时,随的增大而增大.
17(2019·阳江市期中)抛物线的顶点为,它的形状与相同,但开口方向与之相反.
(1)直接写出抛物线的解析式 ;
(2)求抛物线与轴的交点坐标.
次函数y=a(x-h)^2+k的图象和性质
一、单选题(共10小题)
1.(2020·黄冈市期中)抛物线y=3(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(﹣2,﹣5) C.(2,5) D.(2,﹣5)
2.(2019·临海市期末)已知二次函数y=ax2+bx+c的部分图象如图所示,下列关于此函数图象的描述中,错误的是( )
A.对称轴是直线x=1 B.当x<0时,函数y随x增大而增大
C.图象的顶点坐标是(1,4) D.图象与x轴的另一个交点是(4,0)
3.(2019·腾冲市期末)关于二次函数y=(x+1)2的图象,下列说法正确的是( )
A.开口向下 B.经过原点
C.对称轴右侧的部分是下降的 D.顶点坐标是(﹣1,0)
4.(2019·呼和浩特市期中)对于抛物线,下列说法正确的是( )
A.开口向下,顶点坐标 B.开口向上,顶点坐标
C.开口向下,顶点坐标 D.开口向上,顶点坐标
5.(2019·十堰市期中)在平面直角坐标系xOy中,抛物线的顶点坐标是( )
A.(2,-1) B.(-1,-1) C.(1,1) D.(1,-1)
6.(2019·中山市期中)关于函数y=﹣(x+2)2﹣1的图象叙述正确的是( )
A.开口向上 B.顶点(2,﹣1)
C.与y轴交点为(0,﹣1) D.对称轴为直线x=﹣2
7.(2019·海门市期中)当函数y=(x-1)2-2的函数值y随着x的增大而减小时,x的取值范围是( )
A. B. C. D.x为任意实数
8.(2020·义乌市期末)关于y=2(x﹣3)2+2的图象,下列叙述正确的是( )
A.顶点坐标为(﹣3,2) B.对称轴为直线y=3
C.当x≥3时,y随x增大而增大 D.当x≥3时,y随x增大而减小
9.(2019·天津市期末)若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
A.m>1 B.m>0 C.m>-1 D.-1<m<0
10.(2019·南开区期中)若二次函数y=(x﹣m)2﹣1,当x≤3时,y随x的增大而减小,则m的取值范围是( )
A.m=3 B.m>3 C.m≥3 D.m≤3
二、填空题(共5小题)
11.(2018·泰安市期末)设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为_____.
12.(2020·普陀区期末)将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是_____.
13.(2019·济南市期末)抛物线y=x2+4x+3的对称轴是直线______.
14.(2020·中山市期中)若点A(-3,y1)、B(0,y2)是二次函数y=-2(x-1)2+3图象上的两点,那么y1与y2的大小关系是________(填y1>y2、y1=y2或y1<y2).
15.(2018·房山区期末)把二次函数化为的形式,那么=_____.
三、解答题(共2小题)
16.(2018·平度市期末)已知二次函数y=﹣2x2+5x﹣2.
(1)写出该函数的对称轴,顶点坐标;
(2)求该函数与坐标轴的交点坐标.
17.(2018·徽县期中)把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标。
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号 开口方向 顶点坐标 对称轴 性质
向上 x=h 时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下 x=h 时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号 开口方向 顶点坐标 对称轴 性质
向上 x=h 时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下 x=h 时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
【典型例题】
类型一、二次函数图象及性质
1. 二次函数y=﹣(x﹣3)2+2的顶点的坐标是 ,对称轴是 .
举一反三:
【变式】(2014 荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
把抛物线向上平移2个单位,再向左平移4个单位,得到抛物线,求b,c的值.
【变式】二次函数的图象可以看作是二次函数的图象向 平移4个单位,再向 平移3个单位得到的.
类型二、二次函数性质的综合应用
3. 二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
对应练习
二次函数y=a(x-h)^2的图象和性质
精选练习
一、单选题(共10小题)
1.(2019·宣武区期末)抛物线顶点坐标是
A. B. C. D.
2.(2018·临沂市期末)关于抛物线y=﹣2(x﹣1)2说法正确的是( )
A.顶点坐标为(﹣2,1)
B.当x<1时,y随x的增大而增大
C.当x=0时,y有最大值1
D.抛物线的对称轴为直线x=﹣2
3.(2019·琼中县期中)在一次函数y=kx+b(k≠0)中,y随x的增大而减小,则二次函数y=k(x﹣1)2的图象大致是( )
A. B. C. D.
4.(2019·广州市期中)已知抛物线y=(x﹣2)2上任意两点A(x1,y1)与B(x2,y2),若x2>x1>2,则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1≥y2 D.y1≤y2
5.(2019·扬州市期末)函数的图象可以由函数的图象( )得到
A.向左平移3个单位 B.向右平移3个单位
C.向上平移3个单位 D.向下平移3个单位
6.抛物线y= (x 5)2不经过的象限是( )
A.第一、二象限 B.第一、四象限 C.第二、三象限 D.第三、四象限
7.关于抛物线①y=x2;②y=–x2+1;③y=(x–2)2,下列结论正确的是( )
A.顶点相同 B.对称轴相同
C.形状相同 D.都有最高点
8.对于抛物线,下列说法正确的是( )
A.最低点坐标(-3, 0) B.最高点坐标(-3, 0) C.最低点坐标(3, 0) D.最高点坐标(3, 0)
9.顶点为(-5,0),且开口方向、形状与函数的图象相同的抛物线是( )
A. B. C. D.
10.已知函数y=(x﹣1)2,下列结论正确的是( )
A.当x>0时,y随x的增大而减小 B.当x<0时,y随x的增大而增大
C.当x<1时,y随x的增大而减小 D.当x<﹣1时,y随x的增大而增大
二、填空题(共5小题)
11.(2018·洛阳市期末)已知函数y=﹣(x﹣1)2图象上两点A(2,y1),B(a,y2),其中a>2,则y1与y2的大小关系是y1_____y2(填“<”、“>”或“=”)
12.(2019·肇庆市期中)二次函数y=3x2+1和y=3(x﹣1)2,以下说法:
①它们的图象开口方向、大小相同;
②它们的对称轴都是y轴,顶点坐标都是原点(0,1);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们与坐标轴都有一个交点;
其中正确的说法有_____.
13.(2018·厦门市期末)抛物线经过点(-2,1),则______。
14.(2018·鼓楼区期末)已知A(-4,y1),B(-3,y2),C(3,y3)三点都在二次函数y=-2(x+2)2的图象上,则y1,y2,y3的大小关系为___.
15.(2019·中山市期中)点A(﹣1,﹣2)在抛物线y=﹣(x﹣1)2上,点A、B关于该抛物线的对称轴对称,则B点坐标为_____.
三、解答题(共2小题)
16.(2018·揭阳市期末)已知二次函数,当时有最大值,且此函数的图象经过点,求此二次函数的关系式,并指出当为何值时,随的增大而增大.
17(2019·阳江市期中)抛物线的顶点为,它的形状与相同,但开口方向与之相反.
(1)直接写出抛物线的解析式 ;
(2)求抛物线与轴的交点坐标.
次函数y=a(x-h)^2+k的图象和性质
一、单选题(共10小题)
1.(2020·黄冈市期中)抛物线y=3(x﹣2)2+5的顶点坐标是( )
A.(﹣2,5) B.(﹣2,﹣5) C.(2,5) D.(2,﹣5)
2.(2019·临海市期末)已知二次函数y=ax2+bx+c的部分图象如图所示,下列关于此函数图象的描述中,错误的是( )
A.对称轴是直线x=1 B.当x<0时,函数y随x增大而增大
C.图象的顶点坐标是(1,4) D.图象与x轴的另一个交点是(4,0)
3.(2019·腾冲市期末)关于二次函数y=(x+1)2的图象,下列说法正确的是( )
A.开口向下 B.经过原点
C.对称轴右侧的部分是下降的 D.顶点坐标是(﹣1,0)
4.(2019·呼和浩特市期中)对于抛物线,下列说法正确的是( )
A.开口向下,顶点坐标 B.开口向上,顶点坐标
C.开口向下,顶点坐标 D.开口向上,顶点坐标
5.(2019·十堰市期中)在平面直角坐标系xOy中,抛物线的顶点坐标是( )
A.(2,-1) B.(-1,-1) C.(1,1) D.(1,-1)
6.(2019·中山市期中)关于函数y=﹣(x+2)2﹣1的图象叙述正确的是( )
A.开口向上 B.顶点(2,﹣1)
C.与y轴交点为(0,﹣1) D.对称轴为直线x=﹣2
7.(2019·海门市期中)当函数y=(x-1)2-2的函数值y随着x的增大而减小时,x的取值范围是( )
A. B. C. D.x为任意实数
8.(2020·义乌市期末)关于y=2(x﹣3)2+2的图象,下列叙述正确的是( )
A.顶点坐标为(﹣3,2) B.对称轴为直线y=3
C.当x≥3时,y随x增大而增大 D.当x≥3时,y随x增大而减小
9.(2019·天津市期末)若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
A.m>1 B.m>0 C.m>-1 D.-1<m<0
10.(2019·南开区期中)若二次函数y=(x﹣m)2﹣1,当x≤3时,y随x的增大而减小,则m的取值范围是( )
A.m=3 B.m>3 C.m≥3 D.m≤3
二、填空题(共5小题)
11.(2018·泰安市期末)设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为_____.
12.(2020·普陀区期末)将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是_____.
13.(2019·济南市期末)抛物线y=x2+4x+3的对称轴是直线______.
14.(2020·中山市期中)若点A(-3,y1)、B(0,y2)是二次函数y=-2(x-1)2+3图象上的两点,那么y1与y2的大小关系是________(填y1>y2、y1=y2或y1<y2).
15.(2018·房山区期末)把二次函数化为的形式,那么=_____.
三、解答题(共2小题)
16.(2018·平度市期末)已知二次函数y=﹣2x2+5x﹣2.
(1)写出该函数的对称轴,顶点坐标;
(2)求该函数与坐标轴的交点坐标.
17.(2018·徽县期中)把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标。
同课章节目录
