2021-2022学年山东省济宁市任城区六年级(上)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省济宁市任城区六年级(上)期中数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览




文档简介
2021-2022学年山东省济宁市任城区六年级(上)期中数学试卷(五四学制)
一.选择题(共10小题)
1.﹣2的相反数是( )
A.﹣2 B.2 C.﹣ D.
2.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元 B.收入20元 C.支出80元 D.收入80元
3.下列图形中,表示立体图形的个数是( )
A.2个 B.3个 C.4个 D.5个
4.一只海豚从水面先潜入水下40米,然后又上升了23米,此时海豚离水面( )
A.63米 B.17米 C.23米 D.40米
5.用一个平面截长方体,截面可能是下列图形中的( )
①三角形;②正方形;③长方形;④梯形;⑤圆.
A.②③④ B.①②③④ C.②③⑤ D.③④
6.下列计算正确的是( )
A.﹣6+4=﹣10 B.0﹣7=7
C.﹣1.3﹣(﹣2.1)=0.8 D.4﹣(﹣4)=0
7.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A. B. C. D.
8.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
9.小明的爸爸买了一种股票,每股10元,如表记录了在一周内该股票的涨跌的情况(用正数记股价比前一日的上涨数,用负数记股价比前一日的下跌数),该股票这五天中的最高价是( )
星期 一 二 三 四 五
股票跌涨(元) 0.2 0.35 ﹣0.15 0.2 ﹣0.3
A.10.6元 B.10.55元 C.10.4元 D.10.35元
10.在有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有( )
A.4 B.3 C.2 D.1
二.填空题(共5小题)
11.﹣4的倒数是 .
12.地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为 .
13.用四舍五入法对0.03095精确到0.001位的近似值是 .
14.如图所示的圆柱几何体(单位:厘米),则它的的体积是 立方厘米.(结果保留π).
15.一种物质甲在一定波长光的照射下会发生变化(化学上称为反应),变化的速度(反应速度)随着时间的变化为:每隔4分钟反应速度降为原来的一半,如果刚开始的反应速度为80单位/分,则刚满16分钟后的反应速度为 单位/分.
三.解答题(共9小题)
16.计算:
(1)(﹣8)﹣(﹣2).
(2)25+(﹣10).
17.把下列各数填在相应的大括号内:
﹣35,0.1,﹣,0,﹣3,1,4.0100100……,22,﹣0.3,π.
正数:{ ……};
整数:{ ……};
负分数:{ ……};
非负整数:{ ……}.
18.把下列各数在数轴上表示出来,并用“>”把它们连接起来.
3.5,0,﹣|﹣4|,2,﹣2.
19.计算:
(1)(+﹣)×(﹣12);
(2)﹣22÷×(﹣)2.
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
21.一天,某出租车被安排以A地为出发地,只在东西方向道路上营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10.假设该出租车每次乘客下车后,都在停车地等待下一个乘客,直到下一个乘客上车再出发.
(1)将最后一名乘客送到目的地,出租车在A地何处?
(2)若每千米的价格为3元,司机当天的营业额是多少?
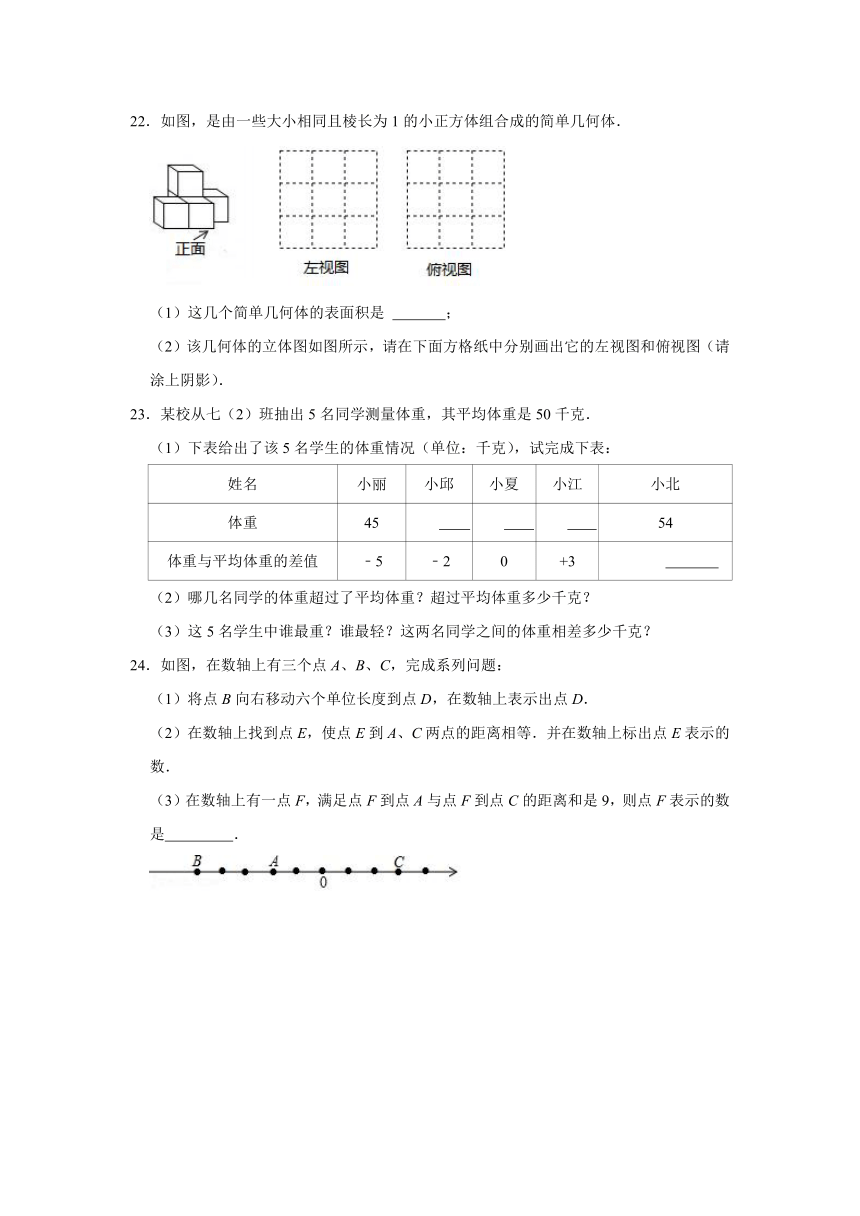
22.如图,是由一些大小相同且棱长为1的小正方体组合成的简单几何体.
(1)这几个简单几何体的表面积是 ;
(2)该几何体的立体图如图所示,请在下面方格纸中分别画出它的左视图和俯视图(请涂上阴影).
23.某校从七(2)班抽出5名同学测量体重,其平均体重是50千克.
(1)下表给出了该5名学生的体重情况(单位:千克),试完成下表:
姓名 小丽 小邱 小夏 小江 小北
体重 45 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3
(2)哪几名同学的体重超过了平均体重?超过平均体重多少千克?
(3)这5名学生中谁最重?谁最轻?这两名同学之间的体重相差多少千克?
24.如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
2021-2022学年山东省济宁市任城区六年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.﹣2的相反数是( )
A.﹣2 B.2 C.﹣ D.
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解答】解:﹣2的相反数是:﹣(﹣2)=2,
故选:B.
2.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元 B.收入20元 C.支出80元 D.收入80元
【分析】因为收入与支出相反,所以由收入100元记作+100元,可得到﹣80元表示支出80元.
【解答】解:如果收入100元记作+100元.那么﹣80元表示支出80元.
故选:C.
3.下列图形中,表示立体图形的个数是( )
A.2个 B.3个 C.4个 D.5个
【分析】利用立体图形的特征判定即可.
【解答】解:根据立体图形的特征可得
第2,第4,第5个图形是立体图形共3个,
故选:B.
4.一只海豚从水面先潜入水下40米,然后又上升了23米,此时海豚离水面( )
A.63米 B.17米 C.23米 D.40米
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【解答】解:水面为0,一只海豚先下潜40m,又上升23m,
故应为﹣40m+23m=﹣17m.
故选:B.
5.用一个平面截长方体,截面可能是下列图形中的( )
①三角形;②正方形;③长方形;④梯形;⑤圆.
A.②③④ B.①②③④ C.②③⑤ D.③④
【分析】用一个平面截长方体,根据截面的形状即可得出答案.
【解答】解:用一个平面截长方体,截面可以是①②③④,
故选:B.
6.下列计算正确的是( )
A.﹣6+4=﹣10 B.0﹣7=7
C.﹣1.3﹣(﹣2.1)=0.8 D.4﹣(﹣4)=0
【分析】根据有理数的加法法则和减法法则逐一计算可得.
【解答】解:A.﹣6+4=﹣2,此选项错误;
B.0﹣7=﹣7,此选项错误;
C.﹣1.3﹣(﹣2.1)=﹣1.3+2.1=0.8,此选项正确;
D.4﹣(﹣4)=4+4=8,此选项错误;
故选:C.
7.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A. B. C. D.
【分析】根据面动成体的原理以及空间想象力即可解.
【解答】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:D.
8.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
【分析】根据正方体的表面展开图的特征进行判断即可.
【解答】解:由正方体表面展开图的“相间、Z端是对面”可知,
“1”与“5”是对面,
“2”与“4”是对面,
“3”与“6”是对面,
故选:A.
9.小明的爸爸买了一种股票,每股10元,如表记录了在一周内该股票的涨跌的情况(用正数记股价比前一日的上涨数,用负数记股价比前一日的下跌数),该股票这五天中的最高价是( )
星期 一 二 三 四 五
股票跌涨(元) 0.2 0.35 ﹣0.15 0.2 ﹣0.3
A.10.6元 B.10.55元 C.10.4元 D.10.35元
【分析】根据有理数的加法法则,可得每天的价格,根据有理数的大小比较法则,可得答案.
【解答】解:一10+0.2=10.2元,二10.2+0.35=10.55元,三10.55﹣0.15=10.4元,四10.4+0.2=10.6元,五10.6﹣0.3=10.3元,
10.6>10.55>10.4>10.3>10.2,
最高价格是10.6元,
故选:A.
10.在有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有( )
A.4 B.3 C.2 D.1
【分析】先化简题目中的数字即可解答本题.
【解答】解:∵﹣12=﹣1,
﹣(﹣1)=1,
﹣|﹣1|=﹣1,
(﹣1)5=﹣1,
∴有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有3个,
故选:B.
二.填空题(共5小题)
11.﹣4的倒数是 .
【分析】根据倒数的定义,直接解答即可.
【解答】解:∵=1,
∴﹣4的倒数是﹣.
12.地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为 1.1×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将110000用科学记数法表示为:1.1×105.
故答案为:1.1×105
13.用四舍五入法对0.03095精确到0.001位的近似值是 0.031 .
【分析】把万分位上的数字9进行四舍五入即可.
【解答】解:0.03095精确到0.001位的近似值是0.031.
故答案为0.031.
14.如图所示的圆柱几何体(单位:厘米),则它的的体积是 24π 立方厘米.(结果保留π).
【分析】利用圆柱体的体积公式V=πr2h,计算即可.
【解答】解:由图可得,圆柱体底面直径为4厘米,高为6厘米,
∴V=πr2h=π×(4÷2)2×6=π×4×6=24π(立方厘米),
故答案为:24π.
15.一种物质甲在一定波长光的照射下会发生变化(化学上称为反应),变化的速度(反应速度)随着时间的变化为:每隔4分钟反应速度降为原来的一半,如果刚开始的反应速度为80单位/分,则刚满16分钟后的反应速度为 5 单位/分.
【分析】设反应速度为v单位/分,反应时间为4t分,由题意可知v=80×()t,再由16=4t,将所求t的值代入即可求解.
【解答】解:设反应速度为v单位/分,反应时间为4t分,
∵每隔4分钟反应速度降为原来的一半,刚开始的反应速度为80单位/分,
∴v=80×()t,
∵16=4t,
∴t=4,
∴v=80×()4=5,
∴16分钟后反应速度为5单位/分,
故答案为5.
三.解答题(共9小题)
16.计算:
(1)(﹣8)﹣(﹣2).
(2)25+(﹣10).
【分析】(1)原式利用减法法则变形,再根据有理数的加法法则得出结果;
(2)根据异号两数相加的法则即可得出结果.
【解答】解:(1)原式=﹣8+2
=﹣(8﹣2)
=﹣6;
(2)原式=+(25﹣10)
=15.
17.把下列各数填在相应的大括号内:
﹣35,0.1,﹣,0,﹣3,1,4.0100100……,22,﹣0.3,π.
正数:{ 0.1,1,4.0100100……,22,π ……};
整数:{ ﹣35,0,1,22 ……};
负分数:{ ﹣,﹣3,﹣0.3 ……};
非负整数:{ 0,1,22 ……}.
【分析】根据有理数的分类可对给出数字进行分类.
【解答】解:正数:{0.1,1,4.0100100……,22,π……};
整数:{﹣35,0,1,22 ……};
负分数:{﹣,﹣3,﹣0.3……};
非负整数:{0,1,22 ……}.
18.把下列各数在数轴上表示出来,并用“>”把它们连接起来.
3.5,0,﹣|﹣4|,2,﹣2.
【分析】先在数轴上表示出各个数,再比较即可.
【解答】解:如图所示:
故.
19.计算:
(1)(+﹣)×(﹣12);
(2)﹣22÷×(﹣)2.
【分析】(1)利用乘法分配律计算即可;
(2)先算乘方,再算乘除即可.
【解答】解:(1)(+﹣)×(﹣12)
=×(﹣12)+×(﹣12)﹣×(﹣12)
=﹣3﹣2+6
=1;
(2)﹣22÷×(﹣)2
=﹣4××
=﹣4.
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
【分析】(1)根据长方体的展开图判断出多余一个正方形;
(2)根据长方形和正方形的面积公式分别列式计算即可得解.
【解答】解:(1)多余一个正方形如图所示:
2)表面积=52×2+8×5×4
=50+160
=210cm2.
故答案为210cm2.
21.一天,某出租车被安排以A地为出发地,只在东西方向道路上营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10.假设该出租车每次乘客下车后,都在停车地等待下一个乘客,直到下一个乘客上车再出发.
(1)将最后一名乘客送到目的地,出租车在A地何处?
(2)若每千米的价格为3元,司机当天的营业额是多少?
【分析】(1)由有理数的和差计算得距离4km,方向位于A地的西边;
(2)由绝对值的几何意义求出路程62km,再由单价、数量和总价的关系求出司机当天的营业额是186元.
【解答】解:(1)∵行车里程依先后次序记录:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10,
∴将最后一名乘客送到目的地出租车在A地位置:
(+9)+(﹣3)+(﹣5)+(+4)+(﹣8)+(+6)+(﹣7)+(﹣6)+(﹣4)+(+10)=﹣4,
∴出租车在A地的西边,距离A地4km;
(2)∵出租车当天所行驶的总路程为:
|+9|+|﹣3|+|﹣5|+|+4|+|﹣8|+|+6|+|﹣7|+|﹣6|+|﹣4|+|+10|=62km,
∴司机当天的营业额为:62×3=186(元).
22.如图,是由一些大小相同且棱长为1的小正方体组合成的简单几何体.
(1)这几个简单几何体的表面积是 22 ;
(2)该几何体的立体图如图所示,请在下面方格纸中分别画出它的左视图和俯视图(请涂上阴影).
【分析】(1)直接利用几何体的表面积求法,分别求出各侧面即可;
(2)利用从不同角度进而得出观察物体进而得出左视图和俯视图.
【解答】解:(1)这个几何体的表面积为2×4+2×4+2×3=22,
故答案为:22.
(2)如图所示:
23.某校从七(2)班抽出5名同学测量体重,其平均体重是50千克.
(1)下表给出了该5名学生的体重情况(单位:千克),试完成下表:
姓名 小丽 小邱 小夏 小江 小北
体重 45 48 50 53 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3 +4
(2)哪几名同学的体重超过了平均体重?超过平均体重多少千克?
(3)这5名学生中谁最重?谁最轻?这两名同学之间的体重相差多少千克?
【分析】(1)由平均体重,再根据各学生体重与平均体重的差值即可填表;
(2)找出正数就是超重的同学体重,超过的体重就是指该正数的绝对值;
(3)找出最重和最轻的体重,直接相减即可求解.
【解答】解:(1)
姓名 小丽 小邱 小夏 小江 小北
体重 45 48 50 53 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3 +4
(2)小江和小北的体重超重,小江超重3千克,小北超重4千克;
(3)小北最重,小丽最轻,这两名同学之间的体重相差54﹣45=9千克.
24.如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 5或﹣4 .
【分析】(1)根据数轴上的点移动时的大小变化规律,即“左减右加”即可得到结论;
(2)根据题意可知点E是线段AC的中点;
(3)根据点F到点A、点C的距离之和是9,即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出结论;
【解答】解:(1)﹣5+6=1;如图.
(2)点E表示的数为(﹣2+3)÷2=1÷2=0.5;如图,
(3)由已知得:|x﹣(﹣2)|+|x﹣3|=9,
解得:x1=5,x2=﹣4.
故答案为:5或﹣4.
一.选择题(共10小题)
1.﹣2的相反数是( )
A.﹣2 B.2 C.﹣ D.
2.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元 B.收入20元 C.支出80元 D.收入80元
3.下列图形中,表示立体图形的个数是( )
A.2个 B.3个 C.4个 D.5个
4.一只海豚从水面先潜入水下40米,然后又上升了23米,此时海豚离水面( )
A.63米 B.17米 C.23米 D.40米
5.用一个平面截长方体,截面可能是下列图形中的( )
①三角形;②正方形;③长方形;④梯形;⑤圆.
A.②③④ B.①②③④ C.②③⑤ D.③④
6.下列计算正确的是( )
A.﹣6+4=﹣10 B.0﹣7=7
C.﹣1.3﹣(﹣2.1)=0.8 D.4﹣(﹣4)=0
7.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A. B. C. D.
8.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
9.小明的爸爸买了一种股票,每股10元,如表记录了在一周内该股票的涨跌的情况(用正数记股价比前一日的上涨数,用负数记股价比前一日的下跌数),该股票这五天中的最高价是( )
星期 一 二 三 四 五
股票跌涨(元) 0.2 0.35 ﹣0.15 0.2 ﹣0.3
A.10.6元 B.10.55元 C.10.4元 D.10.35元
10.在有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有( )
A.4 B.3 C.2 D.1
二.填空题(共5小题)
11.﹣4的倒数是 .
12.地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为 .
13.用四舍五入法对0.03095精确到0.001位的近似值是 .
14.如图所示的圆柱几何体(单位:厘米),则它的的体积是 立方厘米.(结果保留π).
15.一种物质甲在一定波长光的照射下会发生变化(化学上称为反应),变化的速度(反应速度)随着时间的变化为:每隔4分钟反应速度降为原来的一半,如果刚开始的反应速度为80单位/分,则刚满16分钟后的反应速度为 单位/分.
三.解答题(共9小题)
16.计算:
(1)(﹣8)﹣(﹣2).
(2)25+(﹣10).
17.把下列各数填在相应的大括号内:
﹣35,0.1,﹣,0,﹣3,1,4.0100100……,22,﹣0.3,π.
正数:{ ……};
整数:{ ……};
负分数:{ ……};
非负整数:{ ……}.
18.把下列各数在数轴上表示出来,并用“>”把它们连接起来.
3.5,0,﹣|﹣4|,2,﹣2.
19.计算:
(1)(+﹣)×(﹣12);
(2)﹣22÷×(﹣)2.
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
21.一天,某出租车被安排以A地为出发地,只在东西方向道路上营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10.假设该出租车每次乘客下车后,都在停车地等待下一个乘客,直到下一个乘客上车再出发.
(1)将最后一名乘客送到目的地,出租车在A地何处?
(2)若每千米的价格为3元,司机当天的营业额是多少?
22.如图,是由一些大小相同且棱长为1的小正方体组合成的简单几何体.
(1)这几个简单几何体的表面积是 ;
(2)该几何体的立体图如图所示,请在下面方格纸中分别画出它的左视图和俯视图(请涂上阴影).
23.某校从七(2)班抽出5名同学测量体重,其平均体重是50千克.
(1)下表给出了该5名学生的体重情况(单位:千克),试完成下表:
姓名 小丽 小邱 小夏 小江 小北
体重 45 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3
(2)哪几名同学的体重超过了平均体重?超过平均体重多少千克?
(3)这5名学生中谁最重?谁最轻?这两名同学之间的体重相差多少千克?
24.如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
2021-2022学年山东省济宁市任城区六年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一.选择题(共10小题)
1.﹣2的相反数是( )
A.﹣2 B.2 C.﹣ D.
【分析】根据一个数的相反数就是在这个数前面添上“﹣”号,求解即可.
【解答】解:﹣2的相反数是:﹣(﹣2)=2,
故选:B.
2.如果收入100元记作+100元.那么﹣80元表示( )
A.支出20元 B.收入20元 C.支出80元 D.收入80元
【分析】因为收入与支出相反,所以由收入100元记作+100元,可得到﹣80元表示支出80元.
【解答】解:如果收入100元记作+100元.那么﹣80元表示支出80元.
故选:C.
3.下列图形中,表示立体图形的个数是( )
A.2个 B.3个 C.4个 D.5个
【分析】利用立体图形的特征判定即可.
【解答】解:根据立体图形的特征可得
第2,第4,第5个图形是立体图形共3个,
故选:B.
4.一只海豚从水面先潜入水下40米,然后又上升了23米,此时海豚离水面( )
A.63米 B.17米 C.23米 D.40米
【分析】在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.
【解答】解:水面为0,一只海豚先下潜40m,又上升23m,
故应为﹣40m+23m=﹣17m.
故选:B.
5.用一个平面截长方体,截面可能是下列图形中的( )
①三角形;②正方形;③长方形;④梯形;⑤圆.
A.②③④ B.①②③④ C.②③⑤ D.③④
【分析】用一个平面截长方体,根据截面的形状即可得出答案.
【解答】解:用一个平面截长方体,截面可以是①②③④,
故选:B.
6.下列计算正确的是( )
A.﹣6+4=﹣10 B.0﹣7=7
C.﹣1.3﹣(﹣2.1)=0.8 D.4﹣(﹣4)=0
【分析】根据有理数的加法法则和减法法则逐一计算可得.
【解答】解:A.﹣6+4=﹣2,此选项错误;
B.0﹣7=﹣7,此选项错误;
C.﹣1.3﹣(﹣2.1)=﹣1.3+2.1=0.8,此选项正确;
D.4﹣(﹣4)=4+4=8,此选项错误;
故选:C.
7.观察下图,把左边的图形绕着给定的直线旋转一周后可能形成的立体图形是( )
A. B. C. D.
【分析】根据面动成体的原理以及空间想象力即可解.
【解答】解:由图形可以看出,左边的长方形的竖直的两个边与已知的直线平行,因而这两条边旋转形成两个柱形表面,因而旋转一周后可能形成的立体图形是一个管状的物体.
故选:D.
8.图为正方体的展开图,那么在原正方体中与“5”字所在面相对的面上的字为( )
A.1 B.4 C.6 D.3
【分析】根据正方体的表面展开图的特征进行判断即可.
【解答】解:由正方体表面展开图的“相间、Z端是对面”可知,
“1”与“5”是对面,
“2”与“4”是对面,
“3”与“6”是对面,
故选:A.
9.小明的爸爸买了一种股票,每股10元,如表记录了在一周内该股票的涨跌的情况(用正数记股价比前一日的上涨数,用负数记股价比前一日的下跌数),该股票这五天中的最高价是( )
星期 一 二 三 四 五
股票跌涨(元) 0.2 0.35 ﹣0.15 0.2 ﹣0.3
A.10.6元 B.10.55元 C.10.4元 D.10.35元
【分析】根据有理数的加法法则,可得每天的价格,根据有理数的大小比较法则,可得答案.
【解答】解:一10+0.2=10.2元,二10.2+0.35=10.55元,三10.55﹣0.15=10.4元,四10.4+0.2=10.6元,五10.6﹣0.3=10.3元,
10.6>10.55>10.4>10.3>10.2,
最高价格是10.6元,
故选:A.
10.在有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有( )
A.4 B.3 C.2 D.1
【分析】先化简题目中的数字即可解答本题.
【解答】解:∵﹣12=﹣1,
﹣(﹣1)=1,
﹣|﹣1|=﹣1,
(﹣1)5=﹣1,
∴有理数﹣12、﹣(﹣1)、﹣|﹣1|、(﹣1)5中负数有3个,
故选:B.
二.填空题(共5小题)
11.﹣4的倒数是 .
【分析】根据倒数的定义,直接解答即可.
【解答】解:∵=1,
∴﹣4的倒数是﹣.
12.地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为 1.1×105 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将110000用科学记数法表示为:1.1×105.
故答案为:1.1×105
13.用四舍五入法对0.03095精确到0.001位的近似值是 0.031 .
【分析】把万分位上的数字9进行四舍五入即可.
【解答】解:0.03095精确到0.001位的近似值是0.031.
故答案为0.031.
14.如图所示的圆柱几何体(单位:厘米),则它的的体积是 24π 立方厘米.(结果保留π).
【分析】利用圆柱体的体积公式V=πr2h,计算即可.
【解答】解:由图可得,圆柱体底面直径为4厘米,高为6厘米,
∴V=πr2h=π×(4÷2)2×6=π×4×6=24π(立方厘米),
故答案为:24π.
15.一种物质甲在一定波长光的照射下会发生变化(化学上称为反应),变化的速度(反应速度)随着时间的变化为:每隔4分钟反应速度降为原来的一半,如果刚开始的反应速度为80单位/分,则刚满16分钟后的反应速度为 5 单位/分.
【分析】设反应速度为v单位/分,反应时间为4t分,由题意可知v=80×()t,再由16=4t,将所求t的值代入即可求解.
【解答】解:设反应速度为v单位/分,反应时间为4t分,
∵每隔4分钟反应速度降为原来的一半,刚开始的反应速度为80单位/分,
∴v=80×()t,
∵16=4t,
∴t=4,
∴v=80×()4=5,
∴16分钟后反应速度为5单位/分,
故答案为5.
三.解答题(共9小题)
16.计算:
(1)(﹣8)﹣(﹣2).
(2)25+(﹣10).
【分析】(1)原式利用减法法则变形,再根据有理数的加法法则得出结果;
(2)根据异号两数相加的法则即可得出结果.
【解答】解:(1)原式=﹣8+2
=﹣(8﹣2)
=﹣6;
(2)原式=+(25﹣10)
=15.
17.把下列各数填在相应的大括号内:
﹣35,0.1,﹣,0,﹣3,1,4.0100100……,22,﹣0.3,π.
正数:{ 0.1,1,4.0100100……,22,π ……};
整数:{ ﹣35,0,1,22 ……};
负分数:{ ﹣,﹣3,﹣0.3 ……};
非负整数:{ 0,1,22 ……}.
【分析】根据有理数的分类可对给出数字进行分类.
【解答】解:正数:{0.1,1,4.0100100……,22,π……};
整数:{﹣35,0,1,22 ……};
负分数:{﹣,﹣3,﹣0.3……};
非负整数:{0,1,22 ……}.
18.把下列各数在数轴上表示出来,并用“>”把它们连接起来.
3.5,0,﹣|﹣4|,2,﹣2.
【分析】先在数轴上表示出各个数,再比较即可.
【解答】解:如图所示:
故.
19.计算:
(1)(+﹣)×(﹣12);
(2)﹣22÷×(﹣)2.
【分析】(1)利用乘法分配律计算即可;
(2)先算乘方,再算乘除即可.
【解答】解:(1)(+﹣)×(﹣12)
=×(﹣12)+×(﹣12)﹣×(﹣12)
=﹣3﹣2+6
=1;
(2)﹣22÷×(﹣)2
=﹣4××
=﹣4.
20.小明用若干个正方形和长方形准备拼成一个长方体的展开图,拼完后,小明看来看去觉得所拼图形似乎存在问题.
(1)请你帮小明分析一下拼图是否存在问题,若有多余图形,请将多余部分涂黑;若图形不全,则直接在原图中补全;
(2)若图中的正方形边长为5cm,长方形的长为8cm,请计算修正后所折叠而成的长方体的表面积.
【分析】(1)根据长方体的展开图判断出多余一个正方形;
(2)根据长方形和正方形的面积公式分别列式计算即可得解.
【解答】解:(1)多余一个正方形如图所示:
2)表面积=52×2+8×5×4
=50+160
=210cm2.
故答案为210cm2.
21.一天,某出租车被安排以A地为出发地,只在东西方向道路上营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10.假设该出租车每次乘客下车后,都在停车地等待下一个乘客,直到下一个乘客上车再出发.
(1)将最后一名乘客送到目的地,出租车在A地何处?
(2)若每千米的价格为3元,司机当天的营业额是多少?
【分析】(1)由有理数的和差计算得距离4km,方向位于A地的西边;
(2)由绝对值的几何意义求出路程62km,再由单价、数量和总价的关系求出司机当天的营业额是186元.
【解答】解:(1)∵行车里程依先后次序记录:+9、﹣3、﹣5、+4、﹣8、+6、﹣7、﹣6、﹣4、+10,
∴将最后一名乘客送到目的地出租车在A地位置:
(+9)+(﹣3)+(﹣5)+(+4)+(﹣8)+(+6)+(﹣7)+(﹣6)+(﹣4)+(+10)=﹣4,
∴出租车在A地的西边,距离A地4km;
(2)∵出租车当天所行驶的总路程为:
|+9|+|﹣3|+|﹣5|+|+4|+|﹣8|+|+6|+|﹣7|+|﹣6|+|﹣4|+|+10|=62km,
∴司机当天的营业额为:62×3=186(元).
22.如图,是由一些大小相同且棱长为1的小正方体组合成的简单几何体.
(1)这几个简单几何体的表面积是 22 ;
(2)该几何体的立体图如图所示,请在下面方格纸中分别画出它的左视图和俯视图(请涂上阴影).
【分析】(1)直接利用几何体的表面积求法,分别求出各侧面即可;
(2)利用从不同角度进而得出观察物体进而得出左视图和俯视图.
【解答】解:(1)这个几何体的表面积为2×4+2×4+2×3=22,
故答案为:22.
(2)如图所示:
23.某校从七(2)班抽出5名同学测量体重,其平均体重是50千克.
(1)下表给出了该5名学生的体重情况(单位:千克),试完成下表:
姓名 小丽 小邱 小夏 小江 小北
体重 45 48 50 53 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3 +4
(2)哪几名同学的体重超过了平均体重?超过平均体重多少千克?
(3)这5名学生中谁最重?谁最轻?这两名同学之间的体重相差多少千克?
【分析】(1)由平均体重,再根据各学生体重与平均体重的差值即可填表;
(2)找出正数就是超重的同学体重,超过的体重就是指该正数的绝对值;
(3)找出最重和最轻的体重,直接相减即可求解.
【解答】解:(1)
姓名 小丽 小邱 小夏 小江 小北
体重 45 48 50 53 54
体重与平均体重的差值 ﹣5 ﹣2 0 +3 +4
(2)小江和小北的体重超重,小江超重3千克,小北超重4千克;
(3)小北最重,小丽最轻,这两名同学之间的体重相差54﹣45=9千克.
24.如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 5或﹣4 .
【分析】(1)根据数轴上的点移动时的大小变化规律,即“左减右加”即可得到结论;
(2)根据题意可知点E是线段AC的中点;
(3)根据点F到点A、点C的距离之和是9,即可得出关于x的含绝对值符号的一元一次方程,解方程即可得出结论;
【解答】解:(1)﹣5+6=1;如图.
(2)点E表示的数为(﹣2+3)÷2=1÷2=0.5;如图,
(3)由已知得:|x﹣(﹣2)|+|x﹣3|=9,
解得:x1=5,x2=﹣4.
故答案为:5或﹣4.
同课章节目录
