圆周角导学案.

24.1.4 圆周角 第 课时
班级: 姓名： 授课教师： 时间：
学 习目 标:
1． 理解并掌握圆周角的定义
2. 掌握直径（或半圆）所对的圆周角是直角及90°的圆周角所对的弦是直径的性质，并能运用此性质解决问题.
一．自主学习
（一）阅读课本P84-86, 并完成以下各题。
1．圆周角的定义： ，并且两边都与圆相交的角叫做圆周角。
2．定理：在同圆或等圆中， 所对的圆周角相等，都等于这条弧所对的
。
3，推论：（1） （或直径）所对的圆周角是直角， 的圆周角所对的弦 是 。
（2）在同圆或等圆中， 的圆周角所对的 。
4．圆内接多边形：圆内接四边形的 。
（二）预习检测：
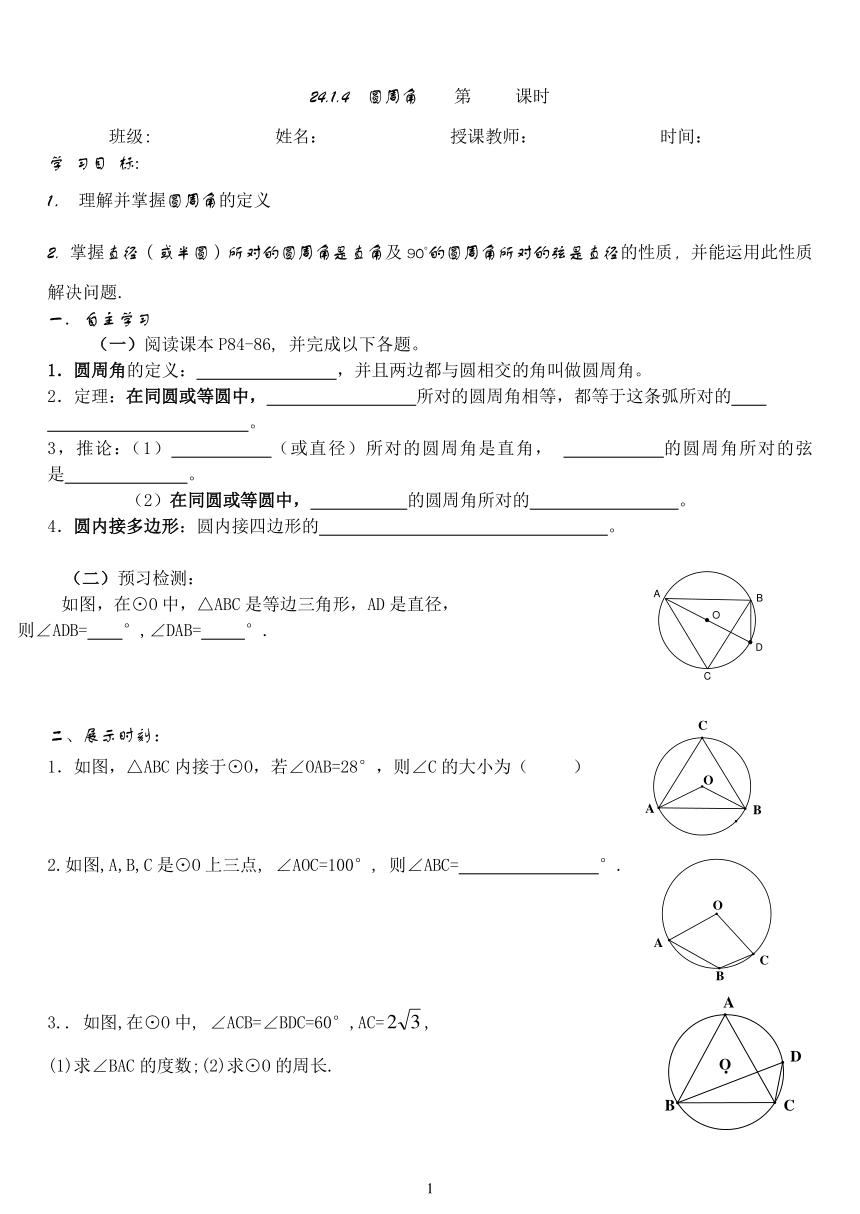
如图，在⊙O中，△ABC是等边三角形，AD是直径，
则∠ADB= °,∠DAB= °.
二、展示时刻：
1．如图，△ABC内接于⊙O，若∠OAB=28°，则∠C的大小为（ ）
2.如图,A,B,C是⊙O上三点, ∠AOC=100°, 则∠ABC= °.
3.. 如图,在⊙O中, ∠ACB=∠BDC=60°,AC=,
(1)求∠BAC的度数;(2)求⊙O的周长.
4、例题分析
例题1.如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，
∠ADC=50°,求∠CEB的度数.
【解析】利用直径所对的圆周角是直角的性质
三、达标检测
1.如图，AB是⊙O的直径，∠A=10°,则∠ABC=________.
2.如图，AB是⊙O的直径，CD是弦，∠ACD=40°,则∠BCD=_______,∠BOD=_______.
3.如图，AB是⊙O的直径，D是⊙O上的任意一点(不与点A、B重合)，延长BD到点C，使DC=BD，判断△ABC的形状：__________。
4.如图，AB是⊙O的直径，AC是弦，∠BAC=30°,则弧AC的度数是( )
A. 30° B. 60° C. 90° D. 120°w w w .x k b 1.c o m ( http: / / www.xkb1.com / )
5、利用三角尺可以画出圆的直径，为什么？你能用这种方法确定一个圆形工件的圆心吗？
四．小结
1,圆周角与圆心角的概念比较接近,因此容易混淆,要结合图形观察角的位置进行判断.
2.一条弦所对的 圆周角有两种(直角除外),一种是锐角，一种是钝角。
3．有关圆的计算常用勾股定理计算，因此构造直角三角形是解题的关键。
4. 直径所对的圆周角是直角是圆中常见辅助线.
五、课后巩固
PAGE
2