华师大版九年级上册24.6.2图形与坐标
文档属性
| 名称 | 华师大版九年级上册24.6.2图形与坐标 |

|
|
| 格式 | zip | ||
| 文件大小 | 877.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-04 12:42:14 | ||
图片预览




文档简介
(共27张PPT)
情境导入
在同一直角坐标系中,图形经过平移、旋转、轴对称、放大或缩小之后,点的坐标会如何变化呢?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
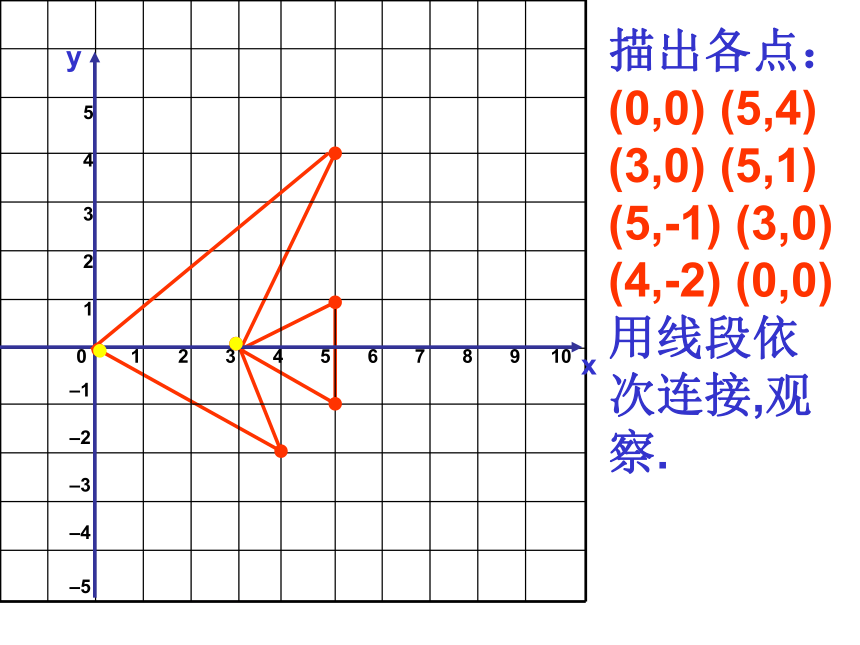
描出各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0) 用线段依次连接,观察.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
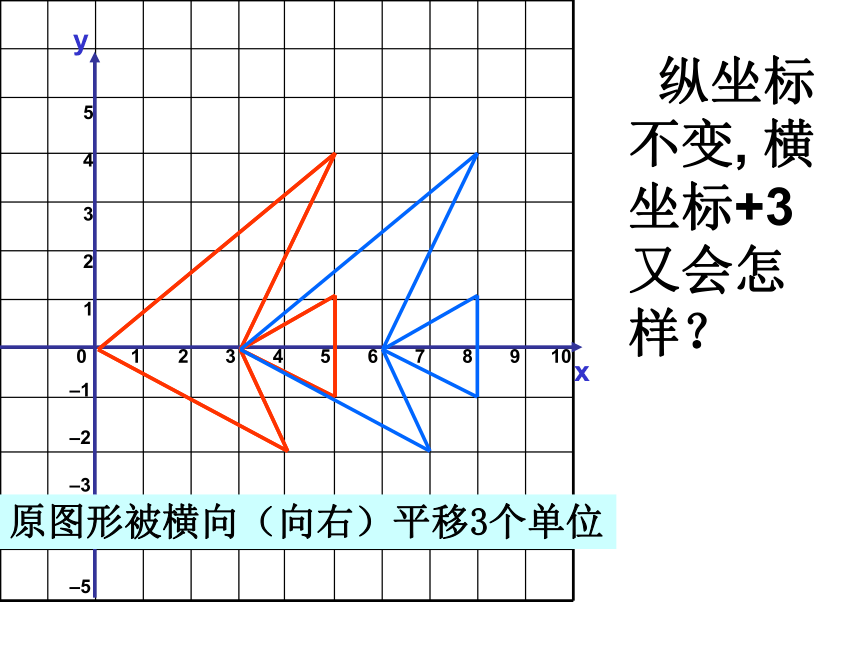
纵坐标不变, 横坐标+3又会怎样?
y
x
原图形被横向(向右)平移3个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
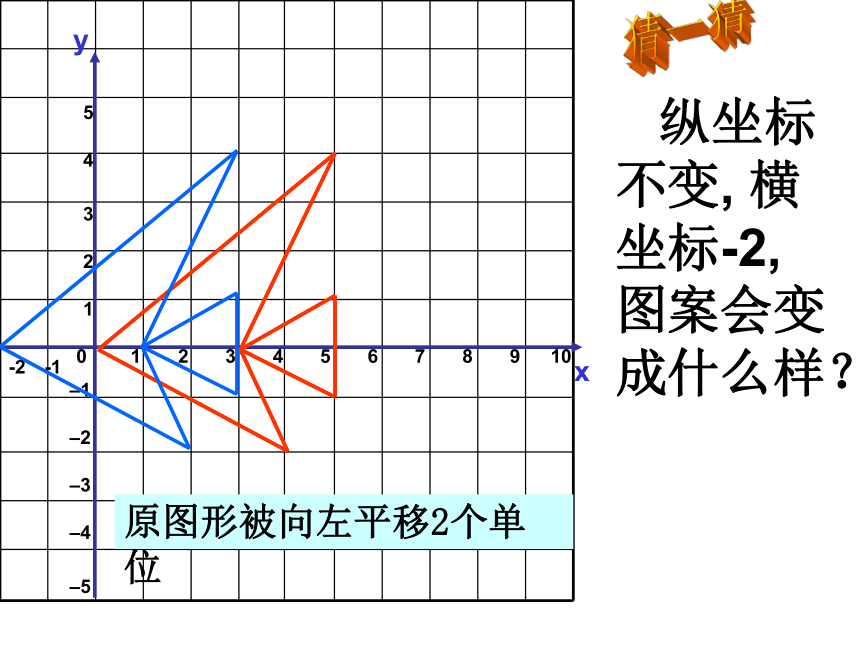
纵坐标不变, 横坐标-2,图案会变成什么样?
y
x
-1
-2
原图形被向左平移2个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
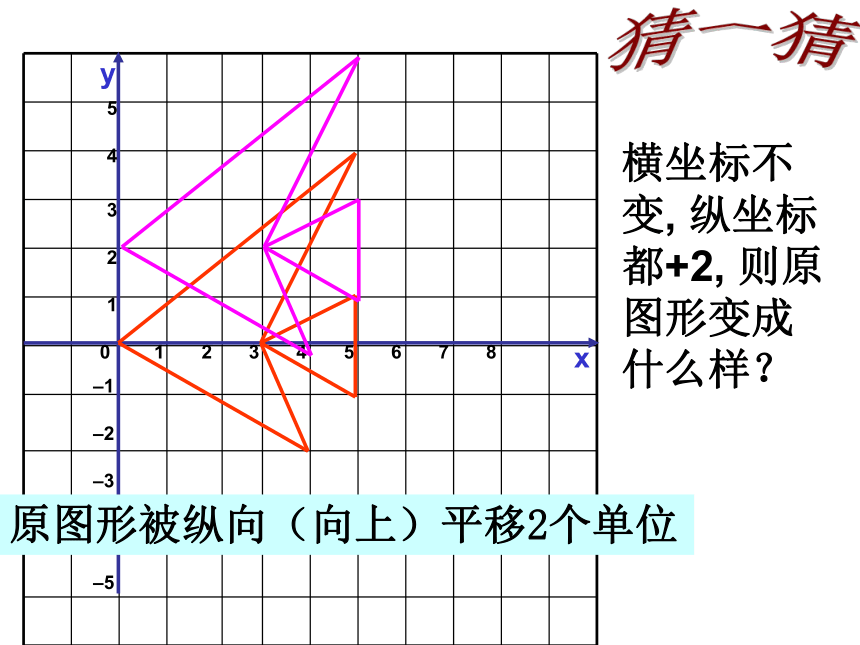
横坐标不变, 纵坐标都+2, 则原图形变成什么样?
y
x
原图形被纵向(向上)平移2个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
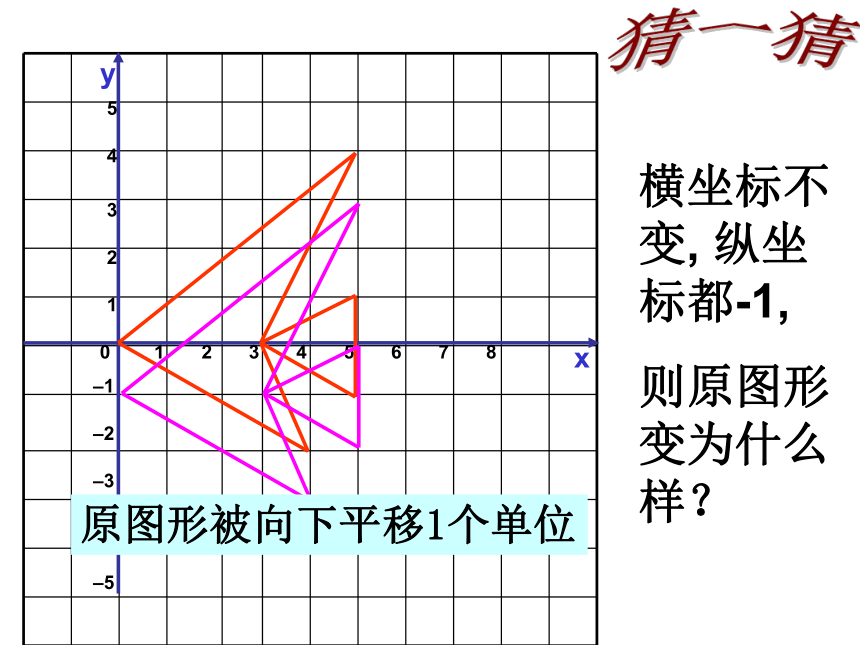
横坐标不变, 纵坐标都-1,
则原图形变为什么样?
y
x
原图形被向下平移1个单位
一、平移
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形_____________
平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形___________
平移a个单位;
向上(向下)
向右(向左)
思考:
经过下列几种变化,所得的图案与原来的图案相比有什么变化 ?
简单表示为:(x,y) (x,y +3).
(x,y) (x +3,y +3).
(x,y) (x +3,y).
你能得到怎样结论?
平移:
(x,y) (x +a,y+b)
沿x轴方向平移|a|个单位:
若a>0,则向右平移;若a<0,则向左平移
沿y轴方向平移|b|个单位:
若b>0,则向上平移;若b<0,则向下平移
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
想一想
与原图形关于y轴对称
纵坐标不变,横坐标乘以-1, 图形会变成什么样?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
纵坐标都乘以-1,横坐标不变,则图形怎么变化?
y
x
与原图形关于x轴对称
–5
纵坐标与横坐标都乘以-1, 图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
与原图形关于原点中心对称
二、轴对称
3.纵坐标不变,横坐标分别乘-1,所得图形与原图形关于 ;
4.横坐标不变,纵坐标分别乘-1,所得图形与原图形关于 ;
三、中心对称
5.横坐标与纵坐标都乘-1,所得图形与原图形关于 中心对称。
Y轴对称
X轴对称
原点
对称:
(x,y) (- x, y)
(x,y) (x, - y)
关于y轴对称;
关于x 轴对称;
(x,y) (-x, - y)
关于原点 对称
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
横坐标与纵坐标同时乘以2,所得图案又会发生什么变化
原图形扩大2倍
原图形的形状没变,面积是原来的4倍。
放大缩小:
(x,y) (k x, ky)
形状不变,放大或缩小k倍;
若k>1,图形整个被放大;
若 01、将坐标作如下变化时,图形将怎样变化?
1. (x,y) (x,y+4)
2. (x,y) (x,y-2)
3. (x,y) (x,-y)
4. (x,y) (3x , y)
6. (x,y) (3x , 3y)
5. (x,y) (x , y)
2.将图中的△ABC作下列运动,画出相应的
图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴正向平移2个单位;
(2)关于y轴对称;
(3)以B点为位似中心,放大到2倍.
·
·
·
·
·
·
x
y
0
2
4
1
6
8
-1
1
2
4
3
5
7
3
5
6
3.两条鱼关于x轴对称;
(x,y) ( __ , __ )
x -y
O
O
X
Y
1
1
X
Y
3
1
4.松树沿x轴方向,向右平移2个单位长度。
(x,y) ( __ , __ )
x+2 y
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) ( x,y+1 )
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) ( -x,-y )
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) (x-2, y )
思 考 与 探 究
下图表示△AOB 和它缩小后得到的△COD,你能求出它们的相似比吗?
方法(一):相似比是对应顶点到位似中心的距离比
方法(二):在同一象限,相似比是对应顶点的同名坐 标比
(1) 平移 图形沿x轴平移,横变(左减右加)纵不变;
图形沿y轴平移,纵变(上加右减)横不变。
直角坐标系中,图形经过平移、对称、放缩的变化,其对应平面的坐标也发生了变化,其变化规律为:
(2) 对称 图形关于x轴对称,横不变,纵为相反数;
图形关于y轴对称,纵不变,横为相反数。
(3) 旋转 图形关于原点对称,横纵皆为相反数。
(4) 位似 以O为位似中心放大或缩小,横纵坐标都扩大或缩小相同的倍数。
情境导入
在同一直角坐标系中,图形经过平移、旋转、轴对称、放大或缩小之后,点的坐标会如何变化呢?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
描出各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0) 用线段依次连接,观察.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
纵坐标不变, 横坐标+3又会怎样?
y
x
原图形被横向(向右)平移3个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
纵坐标不变, 横坐标-2,图案会变成什么样?
y
x
-1
-2
原图形被向左平移2个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
横坐标不变, 纵坐标都+2, 则原图形变成什么样?
y
x
原图形被纵向(向上)平移2个单位
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
横坐标不变, 纵坐标都-1,
则原图形变为什么样?
y
x
原图形被向下平移1个单位
一、平移
1.纵坐标不变,横坐标分别增加(减少)a个单位时,图形_____________
平移 a个 单位;
2.横坐标不变,纵坐标分别增加(减少) a个单位时,图形___________
平移a个单位;
向上(向下)
向右(向左)
思考:
经过下列几种变化,所得的图案与原来的图案相比有什么变化 ?
简单表示为:(x,y) (x,y +3).
(x,y) (x +3,y +3).
(x,y) (x +3,y).
你能得到怎样结论?
平移:
(x,y) (x +a,y+b)
沿x轴方向平移|a|个单位:
若a>0,则向右平移;若a<0,则向左平移
沿y轴方向平移|b|个单位:
若b>0,则向上平移;若b<0,则向下平移
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
y
x
想一想
与原图形关于y轴对称
纵坐标不变,横坐标乘以-1, 图形会变成什么样?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
纵坐标都乘以-1,横坐标不变,则图形怎么变化?
y
x
与原图形关于x轴对称
–5
纵坐标与横坐标都乘以-1, 图形会变成什么样?
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
与原图形关于原点中心对称
二、轴对称
3.纵坐标不变,横坐标分别乘-1,所得图形与原图形关于 ;
4.横坐标不变,纵坐标分别乘-1,所得图形与原图形关于 ;
三、中心对称
5.横坐标与纵坐标都乘-1,所得图形与原图形关于 中心对称。
Y轴对称
X轴对称
原点
对称:
(x,y) (- x, y)
(x,y) (x, - y)
关于y轴对称;
关于x 轴对称;
(x,y) (-x, - y)
关于原点 对称
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
横坐标与纵坐标同时乘以2,所得图案又会发生什么变化
原图形扩大2倍
原图形的形状没变,面积是原来的4倍。
放大缩小:
(x,y) (k x, ky)
形状不变,放大或缩小k倍;
若k>1,图形整个被放大;
若 0
1. (x,y) (x,y+4)
2. (x,y) (x,y-2)
3. (x,y) (x,-y)
4. (x,y) (3x , y)
6. (x,y) (3x , 3y)
5. (x,y) (x , y)
2.将图中的△ABC作下列运动,画出相应的
图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴正向平移2个单位;
(2)关于y轴对称;
(3)以B点为位似中心,放大到2倍.
·
·
·
·
·
·
x
y
0
2
4
1
6
8
-1
1
2
4
3
5
7
3
5
6
3.两条鱼关于x轴对称;
(x,y) ( __ , __ )
x -y
O
O
X
Y
1
1
X
Y
3
1
4.松树沿x轴方向,向右平移2个单位长度。
(x,y) ( __ , __ )
x+2 y
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) ( x,y+1 )
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) ( -x,-y )
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
(x,y) (x-2, y )
思 考 与 探 究
下图表示△AOB 和它缩小后得到的△COD,你能求出它们的相似比吗?
方法(一):相似比是对应顶点到位似中心的距离比
方法(二):在同一象限,相似比是对应顶点的同名坐 标比
(1) 平移 图形沿x轴平移,横变(左减右加)纵不变;
图形沿y轴平移,纵变(上加右减)横不变。
直角坐标系中,图形经过平移、对称、放缩的变化,其对应平面的坐标也发生了变化,其变化规律为:
(2) 对称 图形关于x轴对称,横不变,纵为相反数;
图形关于y轴对称,纵不变,横为相反数。
(3) 旋转 图形关于原点对称,横纵皆为相反数。
(4) 位似 以O为位似中心放大或缩小,横纵坐标都扩大或缩小相同的倍数。
