2021-2022学年华东师大版七年级数学上册《5.2平行线》同步达标测试 (Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学上册《5.2平行线》同步达标测试 (Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 23:31:55 | ||
图片预览

文档简介
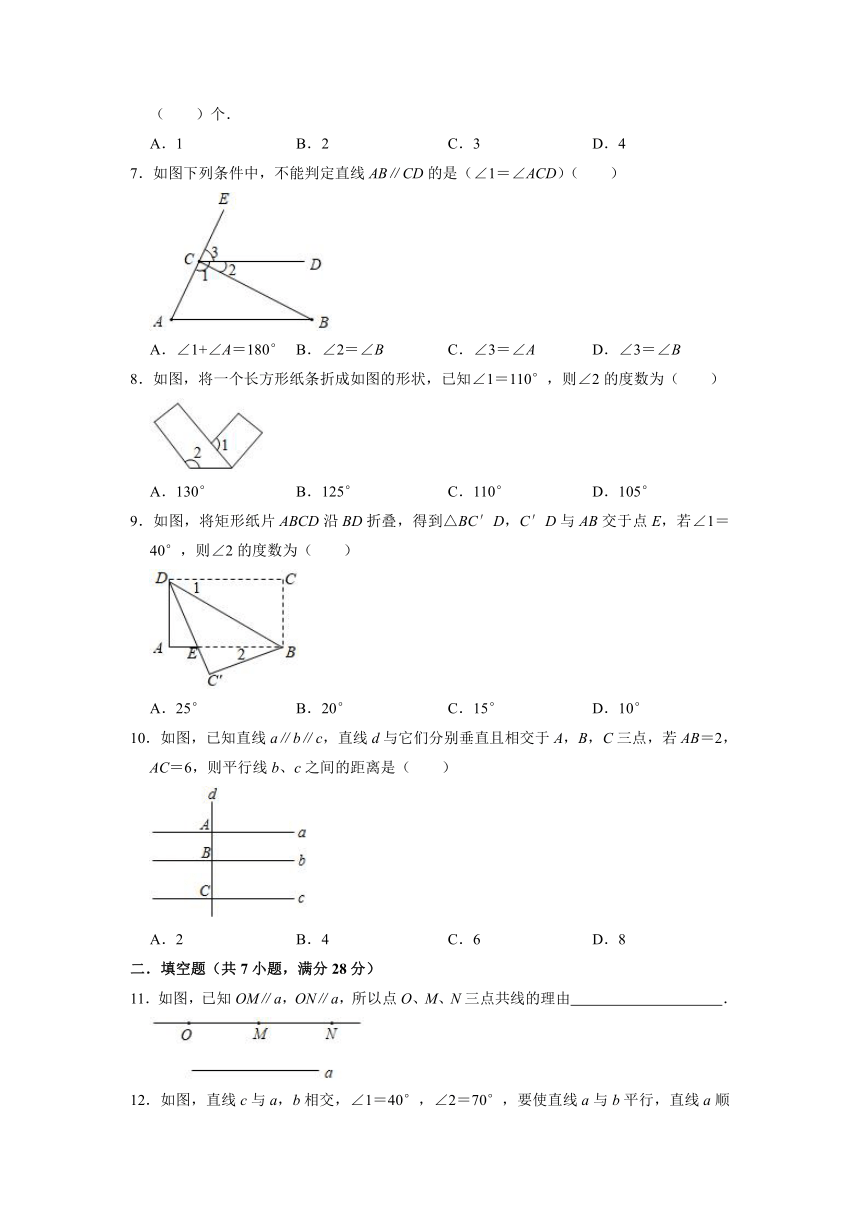
2021-2022学年华师大版七年级数学上册《5.2平行线》同步达标测试(附答案)
一.选择题(共10小题,满分30分)
1.在同一平面内,两条直线可能的位置关系是( )
A.平行 B.相交 C.相交或平行 D.垂直
2.下列说法错误的是( )
A.两点之间线段最短
B.对顶角相等
C.同角的补角相等
D.过一点有且只有一条直线与已知直线平行
3.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠4=180°
4.如图,下列推理中正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵∠BCD+∠ADC=180°,∴AD∥BC
D.∵∠CBA+∠C=180°,∴BC∥AD
5.木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.以上结论都不正确
6.有下列说法:①对顶角相等;②内错角相等;③平面内过一点有且只有一条直线垂直于已知直线;④平面内过一点有且只有一条直线平行于已知直线,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
7.如图下列条件中,不能判定直线AB∥CD的是(∠1=∠ACD)( )
A.∠1+∠A=180° B.∠2=∠B C.∠3=∠A D.∠3=∠B
8.如图,将一个长方形纸条折成如图的形状,已知∠1=110°,则∠2的度数为( )
A.130° B.125° C.110° D.105°
9.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E,若∠1=40°,则∠2的度数为( )
A.25° B.20° C.15° D.10°
10.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是( )
A.2 B.4 C.6 D.8
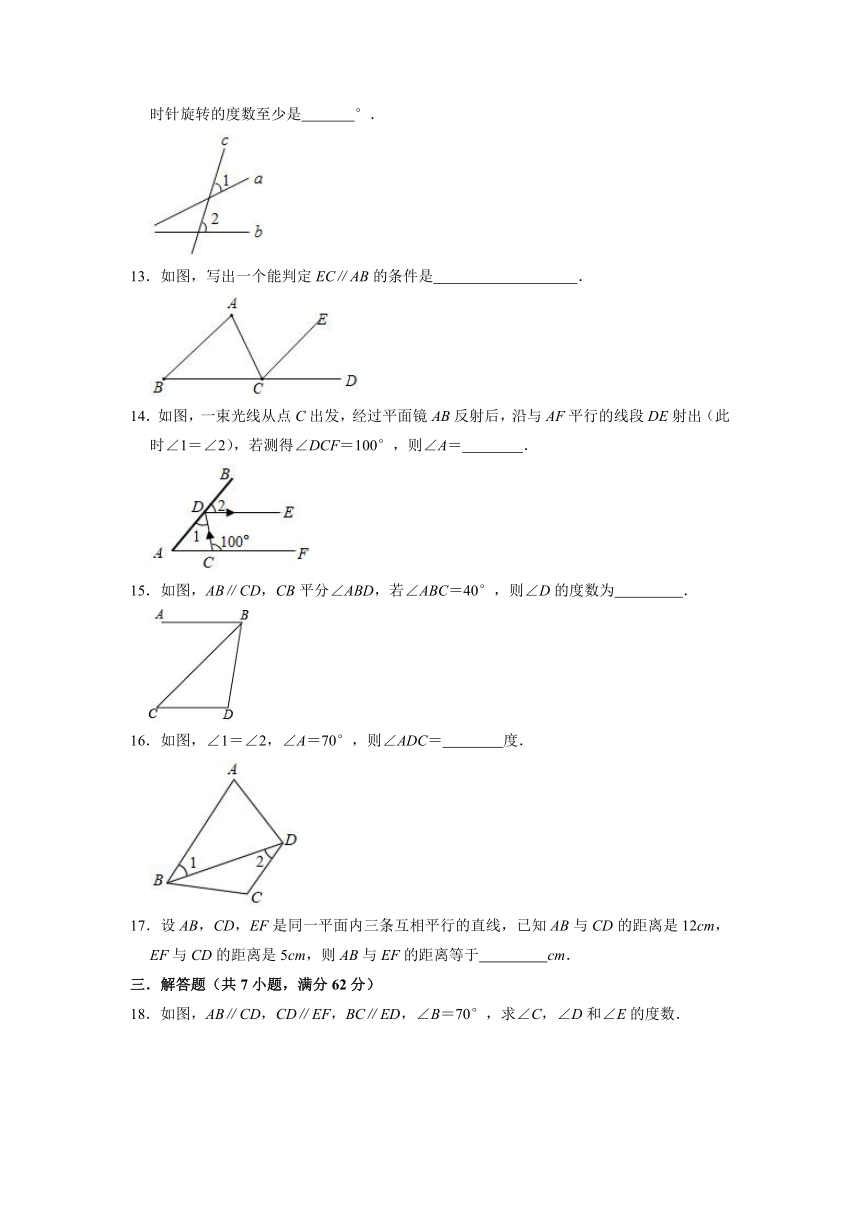
二.填空题(共7小题,满分28分)
11.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
12.如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
13.如图,写出一个能判定EC∥AB的条件是 .
14.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A= .
15.如图,AB∥CD,CB平分∠ABD,若∠ABC=40°,则∠D的度数为 .
16.如图,∠1=∠2,∠A=70°,则∠ADC= 度.
17.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
三.解答题(共7小题,满分62分)
18.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
19.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.
20.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
求证:AB∥CD.
21.“村村通”是国家的一个系统工程,其中包涵公路、电力、生活和饮用水、电话网、有线电视网、互联网等等,现计划在A,B,C周边修公路,公路从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村,那么要想从C村修路CE,沿什么方向修,可以保证CE与AB平行?
22.已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF交AB于点G,且EF∥AD.求证:∠AGF=∠F.
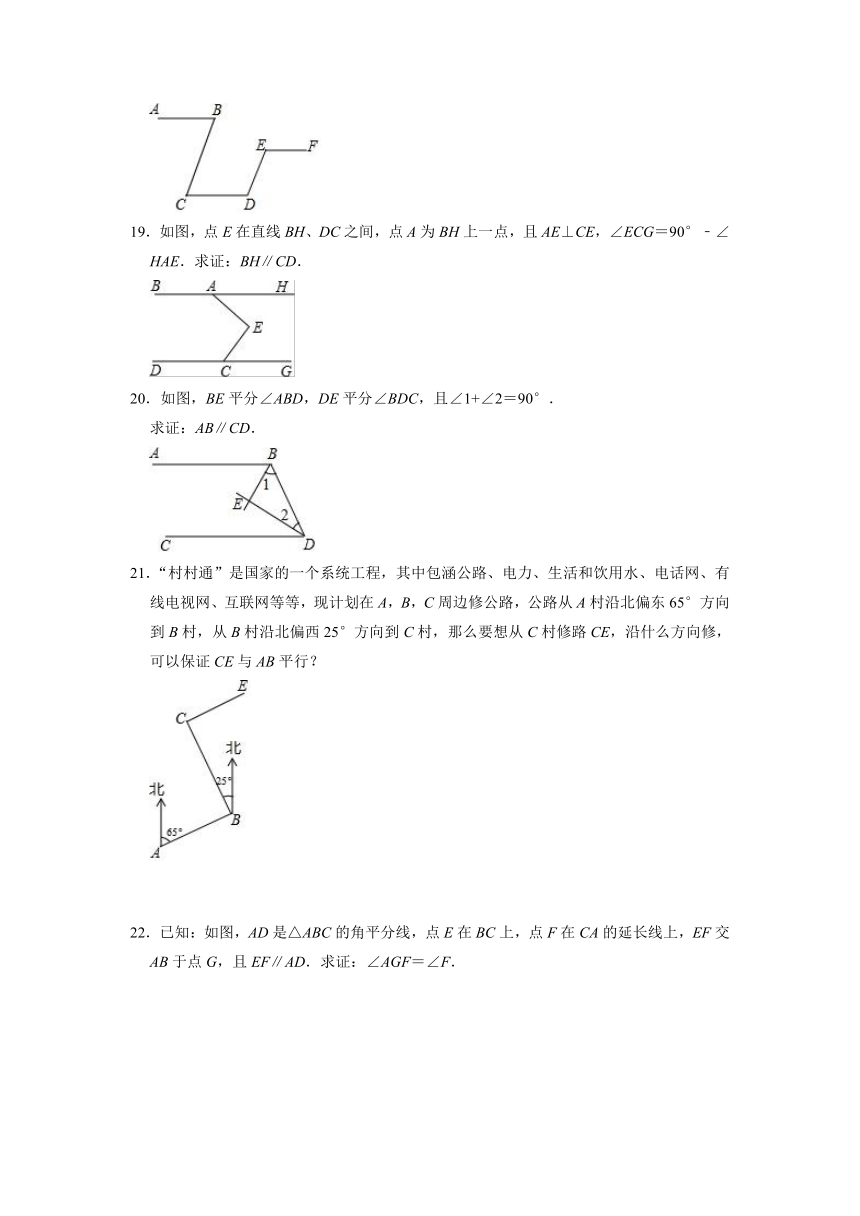
23.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=72°,求∠BAD的度数.
24.已知:如图,AB∥CD,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交,
故选:C.
2.解:A、两点之间线段最短,说法正确.
B、对顶角相等,说法正确.
C、同角的补角相等,说法正确
D、过直线外一点有且只有一条直线与已知直线平行,说法错误.
故选:D.
3.解:由∠1=∠3,可得直线a与b平行,故A能判定;
由∠2+∠4=180°,∠5+∠4=180°,可得∠2=∠5,故直线a与b平行,故B能判定;
由∠1=∠4,∠4=∠3,可得∠1=∠3,故直线a与b平行,故C能判定;
由∠1+∠4=180°,不能判定直线a与b平行,
故选:D.
4.解:A、∵∠1=∠4,∴AB∥CD,故选项错误;
B、∵∠2=∠3,∴BC∥AD,故选项错误;
C、∵∠BCD+∠ADC=180°,∴AD∥BC,故选项正确;
D、∵∠CBA+∠C=180°,∴AB∥CD,故选项错误.
故选:C.
5.解:木工师傅用图中的角尺画平行线,他依据的数学道理是同位角相等,两直线平行,
故选:A.
6.解:①对顶角相等是正确的;
②内错角相等不一定相等,原来的说法错误;
③平面内过一点有且只有一条直线垂直于已知直线是正确的;
④平面内过直线外一点有且只有一条直线平行于已知直线,原来的说法错误.
故选:B.
7.解:A、∵∠1+∠A=180°,可以得到AB∥CD,∴不符合题意,
B、∵∠2=∠B,可以得到AB∥CD,∴不符合题意,
C、∵∠3=∠A,得到AB∥CD,∴不符合题意,
D、∵∠3=∠B,不能得到AB∥CD,∴符合题意,
故选:D.
8.解:如图,
∵EF∥CD,
∴∠1+∠FCD=180°,
∴∠FCD=180°﹣∠1=70°,
∵2∠FCB+∠FCD=180°,
∴∠FCB=55°,
∵AB∥CF,
∴∠2+∠FCB=180°,
∴∠2=180°﹣55°=125°,
故选:B.
9.解:在矩形ABCD中,∠C=90°,AB∥CD,
∴∠1+∠CBD=90°,CD∥AB,
∵∠1=40°,
∴∠CBD=50°,∠ABD=∠1=40°,
由折叠可知:∠2+∠ABD=∠CBD,
∴∠2+∠ABD=50°,
∴∠2=10°.
故选:D.
10.解:∵直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵AB=2,AC=6,
∴BC=6﹣2=4,
即平行线b、c之间的距离是4.
故选:B.
二.填空题(共7小题,满分28分)
11.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
12.解:如图.
∵∠3=∠2=70°时,a∥b,
∴要使直线a与b平行,直线a顺时针旋转的度数至少是70°﹣40°=30°.
故答案为:30.
13.解:∵∠A=∠ACE,
∴EC∥AB(内错角相等,两直线平行).
故答案为:∠A=∠ACE(答案不唯一).
14.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
15.解:∵CB平分∠ABD,
∴∠ABD=2∠ABC=80°,
∵AB∥CD,
∴∠ABD+∠D=180°,
∴∠D=180°﹣80°=100°,
则∠D的度数为100°.
故答案为:100°.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=70°,
∴∠ADC=110°.
故答案为:110.
17.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
三.解答题(共7小题,满分62分)
18.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∴∠C=∠B=70°,∠E=∠D,
又∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠E=180°,
∴∠E=110°.
答:∠C,∠D和∠E的度数分别是70°、110°、110°.
19.证明:过点E作EF∥BH,
∴∠HAE=∠AEF,
∵AE⊥CE,
∴∠AEC=90°
即∠AEF+∠CEF=90°,
∴∠HAE+∠CEF=90°,
∴∠CEF=90°﹣∠HAE,
∵∠ECG=90°﹣∠HAE,
∴∠CEF=∠ECG,
∴EF∥CD,
∵EF∥BH,
∴BH∥CD.
20.解:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
21.解:使CE沿北偏东65°方向(或使CE与CB垂直),
即可保证CE与AB平行.
理由如下:
如图,由题意得,AD∥BF,
∴∠ABF=180°﹣65°=115°,
∴∠ABC=115°﹣25°=90°,
要使CE∥AB,
则∠ECB=∠CBD=90°,
∴CE⊥CB,
则CE应沿北偏东65°方向修.
22.证明:∵EF∥AD,
∴∠F=∠DAC,∠AGF=∠GAD,
∵AD是△ABC的角平分线,
∴∠GAD=∠DAC,
∴∠AGF=∠F.
23.解:(1)AC∥EF.理由:
∵∠1=∠BCE,
∴AD∥CE.
∴∠2=∠4.
∵∠2+∠3=180°,
∴∠4+∠3=180°.
∴EF∥AC.
(2)∵AD∥EC,CA平分∠BCE,
∴∠ACD=∠4=∠2.
∵∠1=72°,
∴∠2=36°.
∵EF∥AC,EF⊥AB于F,
∴∠BAC=∠F=90°.
∴∠BAD=∠BAC﹣∠2
=54°.
24.(1)证明:∵AB∥CD,
∴∠A=∠C ( 两直线平行,内错角相等 ),
又∵∠1=∠A,
∴∠C=∠1,
∴FE∥OC(同位角相等,两直线平行);
(2)解:∵FE∥OC,
∴∠BFE+∠DOC=180°( 两直线平行,同旁内角互补 ),
又∵∠BFE=110°,
∴∠DOC=70°,
∴∠AOB=∠DOC=70°,
∴∠B=180°﹣∠A﹣∠AOB=180°﹣60°﹣70°=50°.
一.选择题(共10小题,满分30分)
1.在同一平面内,两条直线可能的位置关系是( )
A.平行 B.相交 C.相交或平行 D.垂直
2.下列说法错误的是( )
A.两点之间线段最短
B.对顶角相等
C.同角的补角相等
D.过一点有且只有一条直线与已知直线平行
3.如图,直线a、b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.∠1=∠3 B.∠2+∠4=180° C.∠1=∠4 D.∠1+∠4=180°
4.如图,下列推理中正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵∠BCD+∠ADC=180°,∴AD∥BC
D.∵∠CBA+∠C=180°,∴BC∥AD
5.木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.以上结论都不正确
6.有下列说法:①对顶角相等;②内错角相等;③平面内过一点有且只有一条直线垂直于已知直线;④平面内过一点有且只有一条直线平行于已知直线,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
7.如图下列条件中,不能判定直线AB∥CD的是(∠1=∠ACD)( )
A.∠1+∠A=180° B.∠2=∠B C.∠3=∠A D.∠3=∠B
8.如图,将一个长方形纸条折成如图的形状,已知∠1=110°,则∠2的度数为( )
A.130° B.125° C.110° D.105°
9.如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E,若∠1=40°,则∠2的度数为( )
A.25° B.20° C.15° D.10°
10.如图,已知直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,若AB=2,AC=6,则平行线b、c之间的距离是( )
A.2 B.4 C.6 D.8
二.填空题(共7小题,满分28分)
11.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
12.如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
13.如图,写出一个能判定EC∥AB的条件是 .
14.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的线段DE射出(此时∠1=∠2),若测得∠DCF=100°,则∠A= .
15.如图,AB∥CD,CB平分∠ABD,若∠ABC=40°,则∠D的度数为 .
16.如图,∠1=∠2,∠A=70°,则∠ADC= 度.
17.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
三.解答题(共7小题,满分62分)
18.如图,AB∥CD,CD∥EF,BC∥ED,∠B=70°,求∠C,∠D和∠E的度数.
19.如图,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠ECG=90°﹣∠HAE.求证:BH∥CD.
20.如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
求证:AB∥CD.
21.“村村通”是国家的一个系统工程,其中包涵公路、电力、生活和饮用水、电话网、有线电视网、互联网等等,现计划在A,B,C周边修公路,公路从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村,那么要想从C村修路CE,沿什么方向修,可以保证CE与AB平行?
22.已知:如图,AD是△ABC的角平分线,点E在BC上,点F在CA的延长线上,EF交AB于点G,且EF∥AD.求证:∠AGF=∠F.
23.如图,∠1=∠BCE,∠2+∠3=180°.
(1)判断AC与EF的位置关系,并说明理由;
(2)若CA平分∠BCE,EF⊥AB于F,∠1=72°,求∠BAD的度数.
24.已知:如图,AB∥CD,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BFE=110°,∠A=60°,求∠B的度数.
参考答案
一.选择题(共10小题,满分30分)
1.解:在同一个平面内,两条直线只有两种位置关系,即平行或相交,
故选:C.
2.解:A、两点之间线段最短,说法正确.
B、对顶角相等,说法正确.
C、同角的补角相等,说法正确
D、过直线外一点有且只有一条直线与已知直线平行,说法错误.
故选:D.
3.解:由∠1=∠3,可得直线a与b平行,故A能判定;
由∠2+∠4=180°,∠5+∠4=180°,可得∠2=∠5,故直线a与b平行,故B能判定;
由∠1=∠4,∠4=∠3,可得∠1=∠3,故直线a与b平行,故C能判定;
由∠1+∠4=180°,不能判定直线a与b平行,
故选:D.
4.解:A、∵∠1=∠4,∴AB∥CD,故选项错误;
B、∵∠2=∠3,∴BC∥AD,故选项错误;
C、∵∠BCD+∠ADC=180°,∴AD∥BC,故选项正确;
D、∵∠CBA+∠C=180°,∴AB∥CD,故选项错误.
故选:C.
5.解:木工师傅用图中的角尺画平行线,他依据的数学道理是同位角相等,两直线平行,
故选:A.
6.解:①对顶角相等是正确的;
②内错角相等不一定相等,原来的说法错误;
③平面内过一点有且只有一条直线垂直于已知直线是正确的;
④平面内过直线外一点有且只有一条直线平行于已知直线,原来的说法错误.
故选:B.
7.解:A、∵∠1+∠A=180°,可以得到AB∥CD,∴不符合题意,
B、∵∠2=∠B,可以得到AB∥CD,∴不符合题意,
C、∵∠3=∠A,得到AB∥CD,∴不符合题意,
D、∵∠3=∠B,不能得到AB∥CD,∴符合题意,
故选:D.
8.解:如图,
∵EF∥CD,
∴∠1+∠FCD=180°,
∴∠FCD=180°﹣∠1=70°,
∵2∠FCB+∠FCD=180°,
∴∠FCB=55°,
∵AB∥CF,
∴∠2+∠FCB=180°,
∴∠2=180°﹣55°=125°,
故选:B.
9.解:在矩形ABCD中,∠C=90°,AB∥CD,
∴∠1+∠CBD=90°,CD∥AB,
∵∠1=40°,
∴∠CBD=50°,∠ABD=∠1=40°,
由折叠可知:∠2+∠ABD=∠CBD,
∴∠2+∠ABD=50°,
∴∠2=10°.
故选:D.
10.解:∵直线a∥b∥c,直线d与它们分别垂直且相交于A,B,C三点,
∴AB长为直线a和b之间的距离,BC长为直线b和c之间的距离,AC长为直线a和c之间的距离,
又∵AB=2,AC=6,
∴BC=6﹣2=4,
即平行线b、c之间的距离是4.
故选:B.
二.填空题(共7小题,满分28分)
11.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
12.解:如图.
∵∠3=∠2=70°时,a∥b,
∴要使直线a与b平行,直线a顺时针旋转的度数至少是70°﹣40°=30°.
故答案为:30.
13.解:∵∠A=∠ACE,
∴EC∥AB(内错角相等,两直线平行).
故答案为:∠A=∠ACE(答案不唯一).
14.解:∵DE∥AF,
∴∠2=∠A,
∵∠1=∠2,
∴∠1=∠2=∠A,
∵∠DCF=∠A+∠1=2∠A=100°,
∴∠A=50°,
故答案为:50°.
15.解:∵CB平分∠ABD,
∴∠ABD=2∠ABC=80°,
∵AB∥CD,
∴∠ABD+∠D=180°,
∴∠D=180°﹣80°=100°,
则∠D的度数为100°.
故答案为:100°.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=70°,
∴∠ADC=110°.
故答案为:110.
17.解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
三.解答题(共7小题,满分62分)
18.解:∵AB∥CD,CD∥EF,
∴AB∥CD∥EF,
∴∠C=∠B=70°,∠E=∠D,
又∵BC∥DE,
∴∠C+∠D=180°,
∴∠B+∠E=180°,
∴∠E=110°.
答:∠C,∠D和∠E的度数分别是70°、110°、110°.
19.证明:过点E作EF∥BH,
∴∠HAE=∠AEF,
∵AE⊥CE,
∴∠AEC=90°
即∠AEF+∠CEF=90°,
∴∠HAE+∠CEF=90°,
∴∠CEF=90°﹣∠HAE,
∵∠ECG=90°﹣∠HAE,
∴∠CEF=∠ECG,
∴EF∥CD,
∵EF∥BH,
∴BH∥CD.
20.解:∵BE平分∠ABD,DE平分∠BDC(已知),
∴∠ABD=2∠1,∠BDC=2∠2(角平分线定义),
∵∠1+∠2=90°,
∴∠ABD+∠BDC=2(∠1+∠2)=180°,
∴AB∥CD(同旁内角互补,两直线平行).
21.解:使CE沿北偏东65°方向(或使CE与CB垂直),
即可保证CE与AB平行.
理由如下:
如图,由题意得,AD∥BF,
∴∠ABF=180°﹣65°=115°,
∴∠ABC=115°﹣25°=90°,
要使CE∥AB,
则∠ECB=∠CBD=90°,
∴CE⊥CB,
则CE应沿北偏东65°方向修.
22.证明:∵EF∥AD,
∴∠F=∠DAC,∠AGF=∠GAD,
∵AD是△ABC的角平分线,
∴∠GAD=∠DAC,
∴∠AGF=∠F.
23.解:(1)AC∥EF.理由:
∵∠1=∠BCE,
∴AD∥CE.
∴∠2=∠4.
∵∠2+∠3=180°,
∴∠4+∠3=180°.
∴EF∥AC.
(2)∵AD∥EC,CA平分∠BCE,
∴∠ACD=∠4=∠2.
∵∠1=72°,
∴∠2=36°.
∵EF∥AC,EF⊥AB于F,
∴∠BAC=∠F=90°.
∴∠BAD=∠BAC﹣∠2
=54°.
24.(1)证明:∵AB∥CD,
∴∠A=∠C ( 两直线平行,内错角相等 ),
又∵∠1=∠A,
∴∠C=∠1,
∴FE∥OC(同位角相等,两直线平行);
(2)解:∵FE∥OC,
∴∠BFE+∠DOC=180°( 两直线平行,同旁内角互补 ),
又∵∠BFE=110°,
∴∠DOC=70°,
∴∠AOB=∠DOC=70°,
∴∠B=180°﹣∠A﹣∠AOB=180°﹣60°﹣70°=50°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
